黑龙江省大庆市龙凤区2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-03-07 类型:期中考试
一、单选题
-
1. 四个数0,1, , 中,无理数的是( )A、 B、1 C、 D、02. 以下列各组数为边长,不能构成直角三角形的是( )A、 , , B、1,1, C、6,8,10 D、 , ,3. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、4. 利用勾股定理,可以作出长为无理数的线段.如图,在数轴上找到点A,使OA=5,过点A作直线l垂直于OA,在1上取点B,使AB=2,以原点O为圆心,以OB长为半径作弧,弧与数轴的交点为C,那么点C表示的无理数是( )
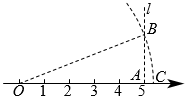 A、 B、 C、7 D、295. 下列各式中正确的是( )A、 B、 C、 D、6. 已经x,y为实数,且 , 则x+y的值为( ).A、-2 B、-8 C、2 D、87. 若n是任意实数,则点N(-1,n2+1)在第( )象限.A、一 B、二 C、三 D、四8. 与最简二次根式是同类二次根式,则a的值为( )A、11 B、3 C、2 D、59. 如图,在四边形中, , , 点是边上一点, , , . 下列结论:①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A、 B、 C、7 D、295. 下列各式中正确的是( )A、 B、 C、 D、6. 已经x,y为实数,且 , 则x+y的值为( ).A、-2 B、-8 C、2 D、87. 若n是任意实数,则点N(-1,n2+1)在第( )象限.A、一 B、二 C、三 D、四8. 与最简二次根式是同类二次根式,则a的值为( )A、11 B、3 C、2 D、59. 如图,在四边形中, , , 点是边上一点, , , . 下列结论:①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )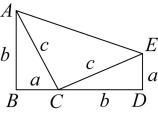 A、2个 B、3个 C、4个 D、5个10. 如图, 为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3 , 再以OA3为直角边作等腰直角三角形OA3A4 , …,按此规律作下去,则OAn的长度为( )
A、2个 B、3个 C、4个 D、5个10. 如图, 为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3 , 再以OA3为直角边作等腰直角三角形OA3A4 , …,按此规律作下去,则OAn的长度为( ) A、( )n B、( )n﹣1 C、( )n D、( )n﹣1
A、( )n B、( )n﹣1 C、( )n D、( )n﹣1二、填空题
-
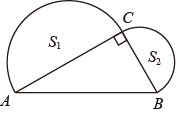
11. 点关于x轴对称点M的坐标为.12. 比较大小: .13. 的算术平方根为.14. 如图,已知在中, , 分别以为直径作半圆,面积分别记为则等于 .
 15. 如图,长方体的底面边长均为3 cm,高为5 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈达到点B,那么所用细线最短需要cm.
15. 如图,长方体的底面边长均为3 cm,高为5 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈达到点B,那么所用细线最短需要cm.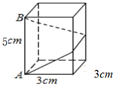 16. 已知5+的整数部分为a,5-的小数部分为b,则a+b的值为17. 如图,正方形ABCD是出四个全等的角三角形围成的,若 , ,则EF的长为。
16. 已知5+的整数部分为a,5-的小数部分为b,则a+b的值为17. 如图,正方形ABCD是出四个全等的角三角形围成的,若 , ,则EF的长为。 18. 如图,△ABC在平面直角坐标系中,AB⊥x轴,BC⊥y轴, , 点B的坐标为 . 将△ABC沿AC折叠得到△ADC,点B落在点D的位置,AD交y轴于点E,则点D的坐标为 .
18. 如图,△ABC在平面直角坐标系中,AB⊥x轴,BC⊥y轴, , 点B的坐标为 . 将△ABC沿AC折叠得到△ADC,点B落在点D的位置,AD交y轴于点E,则点D的坐标为 .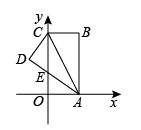
三、解答题
-
19. 计算(1)、;(2)、;(3)、 .(4)、20. 如图,在△ABC中,点D是BC边上一点,连接AD,若AB=10,AC=17,BD=6,AD=8.
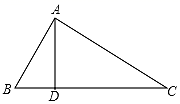 (1)、求∠ADB的度数;(2)、求BC的长.21. 已知数a,b,c在数轴上的位置如图所示:
(1)、求∠ADB的度数;(2)、求BC的长.21. 已知数a,b,c在数轴上的位置如图所示:
化简:
22. 已知点 , 求分别满足下列条件的a的值及点A的坐标.(1)、点A在x轴上;(2)、点A在y轴上;23. 某公司的大门如图所示,其中四边形ABCD是长方形,上部是以AD为直径的半圆,其中AB=2.3m,BC=2m,现有一辆装满货物的卡车,高为2.5m,宽为1.6m,问这辆卡车能否通过公司的大门?并说明你的理由.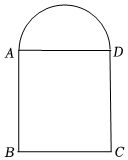 24. 如图,△ABC三个顶点的坐标分别为、、 .
24. 如图,△ABC三个顶点的坐标分别为、、 .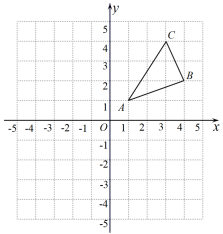 (1)、若与△ABC关于y轴成轴对称,则三个顶点坐标分别为: , ;(2)、若P为y轴上一点,则的最小值为;(3)、计算的面积.25. 阅读与思考
(1)、若与△ABC关于y轴成轴对称,则三个顶点坐标分别为: , ;(2)、若P为y轴上一点,则的最小值为;(3)、计算的面积.25. 阅读与思考两点之间的距离公式
如果数轴上的点 , 分别表示实数 , , 两点 , 间的距离记作 , 那么 .
对于平面上的两点 , 间的距离是否有类似的结论呢?
运用勾股定理,就可以推出平面上两点之间的距离公式.
(1)、如图,平面上两点 , , 求A,B两点之间的距离?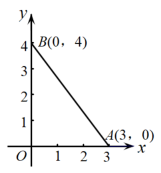 (2)、如图,平面上两点 , , 求这两点之间的距离?
(2)、如图,平面上两点 , , 求这两点之间的距离?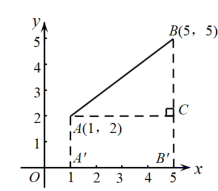 (3)、一般地,设平面上任意两点和 , 如图,如何计算A,B两点之间的距离?
(3)、一般地,设平面上任意两点和 , 如图,如何计算A,B两点之间的距离?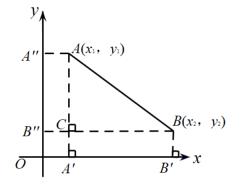
对于问题3,作轴,轴,垂足分别为点 , ;作轴,垂足为;作 , 垂足为点C,且延长BC与y轴交于点 , 则四边形 , 是长方形.
∵ , ,
∴ .
∴ .
这就是平面直角坐标系中两点之间的距离公式.
(4)、思考求下列两点之间的距离:, ;
26. 【阅读材料】材料一:把分母中的根号化去,使分母转化为有理数的过程,叫做分母有理化通常把分子、分母乘以同一个不等于0的式子,以达到化去分母中根号的目的
例如:化简
解:
材料二:化简的方法:如果能找到两个实数m,n,使 , 并且 ,
那么
例如:化简
解:
(1)、【理解应用】填空:化简的结果等于;
(2)、计算:①;
② .
27. 如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,若点B的坐标为(a,b),且b= . (1)、直接写出点A、B、C的坐标;(2)、若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;(3)、在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.28. 已知 和 都是等腰直角三角形 , .
(1)、直接写出点A、B、C的坐标;(2)、若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;(3)、在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.28. 已知 和 都是等腰直角三角形 , .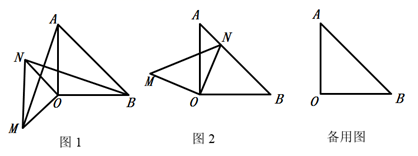 (1)、如图1:连 ,求证: ;(2)、若将 绕点O顺时针旋转,
(1)、如图1:连 ,求证: ;(2)、若将 绕点O顺时针旋转,①如图2,当点N恰好在 边上时,求证: ;
②当点 在同一条直线上时,若 ,请直接写出线段 的长.