安徽省芜湖市市区2021-2022学年七年级下学期期中考试数学试题
试卷更新日期:2023-03-07 类型:期中考试
一、单选题
-
1. 如图所示的四个图形中,不能通过基本图形平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在实数中,最小的是( )A、 B、 C、 D、3. 如图,下列结论正确的是( )
2. 在实数中,最小的是( )A、 B、 C、 D、3. 如图,下列结论正确的是( )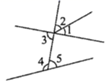 A、 和 是同旁内角 B、 和 是对顶角 C、 和 是内错角 D、 和 是同位角4. 下列式子正确的是( )A、±=7 B、 C、=±5 D、=-35. 如图,将一个长方形纸条折成如图的形状,若已知 , 则的度数为( )
A、 和 是同旁内角 B、 和 是对顶角 C、 和 是内错角 D、 和 是同位角4. 下列式子正确的是( )A、±=7 B、 C、=±5 D、=-35. 如图,将一个长方形纸条折成如图的形状,若已知 , 则的度数为( ) A、63° B、54° C、72° D、45°6. 估算 的值是在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 已知点 . 若点到两坐标轴的距离相等,则a的值为( )A、4 B、-6 C、-1或4 D、-6或8.
A、63° B、54° C、72° D、45°6. 估算 的值是在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 已知点 . 若点到两坐标轴的距离相等,则a的值为( )A、4 B、-6 C、-1或4 D、-6或8.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
 A、5050m2 B、5000m2 C、4900m2 D、4998m29. 如图,AB∥CD,BF,DF 分别平分∠ABE 和∠CDE,BF∥DE,∠F 与∠ABE 互补,则∠F 的度数为
A、5050m2 B、5000m2 C、4900m2 D、4998m29. 如图,AB∥CD,BF,DF 分别平分∠ABE 和∠CDE,BF∥DE,∠F 与∠ABE 互补,则∠F 的度数为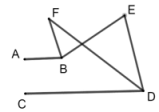 A、30° B、35° C、36° D、45°10. 如图,已知射线 , , 依次作出的角平分线 , 的角平分线 , 的角平分线的角平分线 , 其中点都在射线上,则的度数为( )
A、30° B、35° C、36° D、45°10. 如图,已知射线 , , 依次作出的角平分线 , 的角平分线 , 的角平分线的角平分线 , 其中点都在射线上,则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的立方根是.
12. 如图,A处在B处的北偏东45°方向,C处在A处的南偏东15°方向,则∠BAC等于°. 13. 已知5+的整数部分为a,5-的小数部分为b,则a+b的值为14. 如图,点P、Q分别在一组平行直线、上,在两直线间取一点E使得 , 点F、G分别在、的角平分线上,且点F、G均在平行直线、之间,则 .
13. 已知5+的整数部分为a,5-的小数部分为b,则a+b的值为14. 如图,点P、Q分别在一组平行直线、上,在两直线间取一点E使得 , 点F、G分别在、的角平分线上,且点F、G均在平行直线、之间,则 . 15. 计算= .
15. 计算= .三、解答题
-
16. 如图,已知三角形ABC,把三角形ABC先向上平移3个单位长度,再向右平移2个单位长度,得到三角形 .
 (1)、在图中画出三角形 , 并写出的坐标;(2)、连接 , 求的面积;(3)、在y轴上是否存在一点P,使得与面积相等?若存在请直接写出点P的坐标;若不存在,请说明理由.17. 已知2a+1的平方根是±5,a+b+7的算术平方根为4.(1)、求a、b的值;(2)、求a+b的平方根.18. 如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF,已知BE=6,FE=10,CG=3.求阴影部分的面积.
(1)、在图中画出三角形 , 并写出的坐标;(2)、连接 , 求的面积;(3)、在y轴上是否存在一点P,使得与面积相等?若存在请直接写出点P的坐标;若不存在,请说明理由.17. 已知2a+1的平方根是±5,a+b+7的算术平方根为4.(1)、求a、b的值;(2)、求a+b的平方根.18. 如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF,已知BE=6,FE=10,CG=3.求阴影部分的面积.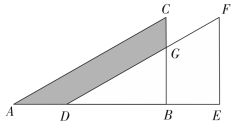 19. 已知,如图, , ∠DAC=120°,∠ACF=20°,∠EFC=140°.
19. 已知,如图, , ∠DAC=120°,∠ACF=20°,∠EFC=140°.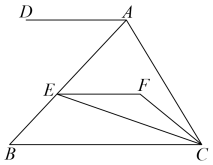 (1)、求证:;(2)、连接CE,若CE平分∠BCF,求∠FEC的度数.20. 阅读下面的推理过程,在括号里或横线上填写结论或理由
(1)、求证:;(2)、连接CE,若CE平分∠BCF,求∠FEC的度数.20. 阅读下面的推理过程,在括号里或横线上填写结论或理由 如图, , 平分 , 平分 , 求证: .
如图, , 平分 , 平分 , 求证: . 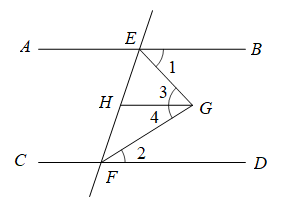
完成下面的证明:
证明:∵(已知),
∴ . ( )
又∵(已知),
∴ . ( )
∵(已知),
∴ ▲ . ( )
∵EG平分(已知),FG平分(已知),
∴ ▲ . ▲ . ( )
∴( + ),即 ,
∴( ),即
21. 将一副三角板中的两个直角顶点 叠放在一起(如图①),其中 , , . (1)、猜想 与 的数量关系,并说明理由;(2)、若 ,求 的度数;(3)、若按住三角板 不动,绕顶点 转动三角 ,试探究 等于多少度时 ,并简要说明理由.22. 在平面直角坐标系中,对于点A(x,y),若点B的坐标为(x+ay,ax+y),则称点B是点A的a级亲密点.例如:点A(-2,6)的级亲密点为B , 即点B的坐标为(1,5).(1)、已知点C(-1,5)的3级亲密点是点D,则点D的坐标为 .(2)、已知点M(m-1,2m)的-3级亲密点M1位于y轴上,求点M1的坐标.(3)、若点E在x轴上,点E不与原点重合,点E的a级亲密点为点F,且EF的长度为OE长度的倍,求a的值.23. 阅读下面材料:
(1)、猜想 与 的数量关系,并说明理由;(2)、若 ,求 的度数;(3)、若按住三角板 不动,绕顶点 转动三角 ,试探究 等于多少度时 ,并简要说明理由.22. 在平面直角坐标系中,对于点A(x,y),若点B的坐标为(x+ay,ax+y),则称点B是点A的a级亲密点.例如:点A(-2,6)的级亲密点为B , 即点B的坐标为(1,5).(1)、已知点C(-1,5)的3级亲密点是点D,则点D的坐标为 .(2)、已知点M(m-1,2m)的-3级亲密点M1位于y轴上,求点M1的坐标.(3)、若点E在x轴上,点E不与原点重合,点E的a级亲密点为点F,且EF的长度为OE长度的倍,求a的值.23. 阅读下面材料:小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断、、三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
 (1)、请回答:、、三个角之间的数量关是.(2)、参考小亮思考问题的方法,解决问题:
(1)、请回答:、、三个角之间的数量关是.(2)、参考小亮思考问题的方法,解决问题:如图2,将沿BA方向平移到(共线), , AC与DF相交于点G,GP、EP分别平分相交于点P,求的度数;
(3)、如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,作和的平分线交于点M,若 , 求(用含的式子表示).