安徽省六安市霍邱县2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-07 类型：期中考试

进入出卷网下载

一、单选题

1. 9的算术平方根是（）

A、3 B、-3 C、±3 D、81

查看试题解析
2. 下列实数中，最大的数是（）

A、 $π$ B、 $\sqrt{2}$ C、 $| - 2 |$ D、3

查看试题解析
3. 下列各式中计算结果为 $x^{6}$ 的是（）

A、 $x^{2} + x^{4}$ B、 $x^{8} - x^{2}$ C、 $x^{2} \cdot x^{4}$ D、 $x^{12} \div x^{2}$

查看试题解析
4. 一个不等式的解在数轴上表示如图，则这个不等式可以是（）

A、 $x + 2 > 0$ B、 $x - 2 < 0$ C、 $2 x \geq 4$ D、 $2 - x < 0$

查看试题解析
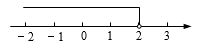5. 已知 $a > b$ ，有下列不等式：（1） $a - 5 > b - 5$ （2） $- 5 a < - 5 b$ （3） $\frac{a}{c} > \frac{b}{c}$ （4） $a + c > b + c$ 其中一定成立的有几个?（）

A、1 B、2 C、3 D、4

查看试题解析
6. 若 $(- 4 b + 3 a)^{2} - (3 a + 4 b)^{2} = 48$ ，则ab=（）

A、-2 B、-1 C、1 D、2

查看试题解析
7. 已知 $a$ ， $b$ 是两个连续整数， $a < \sqrt{3} - 1 < b$ ，则 $a$ ， $b$ 分别是（）

A、-2，-1 B、-1，0 C、0，1 D、1，2

查看试题解析
8. 如果一个正方体的体积变为原来的64倍，那么它的棱长增加为原来的多少倍?（）

A、3 B、4 C、6 D、8

查看试题解析
9. 已知 $9^{m} = 3 ， 27^{n} = 4$ ，则 $3^{2 m + 3 n} =$ （）

A、1 B、6 C、7 D、12

查看试题解析
10. 关于x的不等式组 ${\begin{array}{l} - (x - a) ＜ 3 \\ \frac{1 + 2 x}{3} \geq x - 1 \end{array}$ 恰有2个整数解，则a的取值范围是（）

A、 $a < 6$ B、 $a > 5$ C、 $5 < a < 6$ D、 $5 \leq a < 6$

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{27} =$ ．

查看试题解析
12. 纳秒 $(n s)$ 是非常小的时间单位， $1 n s = 10^{- 9} s$ ，北斗全球导航系统的授时精度优于 $20 n s$ ，用科学记数法表示 $20 n s$ 是.

查看试题解析
13. 《西游记》、《三国演义》、《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著某兴趣小组阅读四大名著的人数，同时满足以下三个条件：
⑴阅读过《西游记》的人数多于阅读过《水浒传》的人数；
⑵阅读过《水浒传》的人数多于阅读过《三国演义》的人数；
⑶阅读过《三国演义》的人数的2倍多于阅读过《西游记》的人数．
若阅读过《三国演义》的人数为4，则阅读过《水浒传》的人数的最大值为．

查看试题解析
14. 定义运算a $\otimes$ b＝a(1－b)，下面给出了关于这种运算的四个结论：
①2 $\otimes$ (－2)＝6； ②a $\otimes$ b＝b $\otimes$ a；③若a＋b＝0，则(a $\otimes$ a)＋(b $\otimes$ b)＝2ab； ④若a $\otimes$ b＝0，则a＝0．其中正确结论的序号是(填上你认为所有正确结论的序号)．

查看试题解析

三、解答题

15. 计算：

(1)、 ${(- \frac{2}{3})}^{0} \times 4^{- 2} \times \sqrt{16}$

(2)、 $a^{2} b^{3} - 2 a (4 a b^{3})$

查看试题解析
16. 计算：

(1)、 $999 \times 1001$

(2)、 $(a + 2 b + 3 c) (a - 3 c + 2 b)$

查看试题解析
17. 把三个半径分别是3，4，5的铅球熔化后做一个更大的铅球，这个大铅球的半径是多少?（球的体积公式是 $V = \frac{4}{3} π R^{3}$ ，其中R是球的半径．）

查看试题解析
18. 先化简，再求值， $(a - b) (a^{2} + a b + b^{2}) + 2 b^{3}$ ，其中 $a = - 2$ ， $b = 3$ ．

查看试题解析
19. 观察下列关于自然数的等式：
① $4^{2} - 1 = 3 \times 5$ ；
② $6^{2} - 3^{2} = 3 \times 9$ ；
③ $8^{2} - 5^{2} = 3 \times 13$ ；
……
根据上述规律解决下列问题：

(1)、写出第四个等式：

(2)、写出你猜想的第n个等式（用含n的式子表示），并说明其正确性．

查看试题解析
20. 甲、乙两个长方形的边长如图所示（m为正实数），其面积分别为 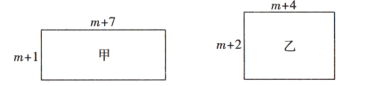$S_{1}$ ， $S_{2}$ ．

(1)、填空： $S_{1} - S_{2} =$ （用含m的代数式表示）；

(2)、若一个正方形的周长等于甲、乙两个长方形的周长之和．
①设该正方形的边长为x，求x的值（用含m的代数式表示）；
②设该正方形的面积为 $S_{3}$ ，试探究： $S_{3}$ 与 $2 (S_{1} + S_{2})$ 的差是否是常数?若是常数，求出这个常数，若不是常数，请说明理由．

查看试题解析
21. 已知 $a^{2} + b^{2} + c^{2} = 20$ ， $a b + a c + b c = 8$ ，求 $(a + b + c)^{2}$ 的值．

查看试题解析
22. 2021年5月7日，《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果．祖冲之是我国南北朝时期杰出的数学家，他是第一个将圆周率 $π$ 精确到小数点后第七位的人，他给出 $π$ 的两个分数形式： $\frac{22}{7}$ （约率）和 $\frac{355}{113}$ （密率）．同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数x的不足近似值和过剩近似值分别为 $\frac{b}{a}$ 和 $\frac{d}{c}$ （即有 $\frac{b}{a} < x < \frac{d}{c}$ ，其中a，b，c，d为正整数），则 $\frac{b + d}{a + c}$ 是x的更为精确的近似值．例如：已知 $\frac{157}{50} < π < \frac{22}{7}$ ，则利用一次“调日法”后可得到 $π$ 的一个更为精确的近似分数为： $\frac{157 + 22}{50 + 7} = \frac{179}{57}$ ；由于 $\frac{179}{57} \approx 3.1404 < π$ ，再由 $\frac{179}{57} < π < \frac{22}{7}$ ，可以再次使用“调日法”得到 $π$ 的更为精确的近似分数…．现已知 $\frac{7}{5} < \sqrt{2} < \frac{3}{2}$ ，求使用两次“调日法可得到 $\sqrt{2}$ 的近似分数．（注： $\sqrt{2} = 1.4142135 \cdot \cdot \cdot$ ）

查看试题解析
23. 某农谷生态园响应国家发展有机农业政策，大力种植有机蔬菜，某超市看好甲、乙两种有机蔬菜的市场价值，经调查甲种蔬菜进价每千克m元，售价每千克16元；乙种蔬菜进价每千克n元，售价每千克18元．

(1)、该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元；购进甲种蔬菜10千克和乙种蔬菜8千克需要212元．求m，n的值．

(2)、该超市决定每天购进甲、乙两种蔬菜共100千克，且投入资金不少于1160元又不多于1168元，设购买甲种蔬菜x千克，求有哪几种购买方案

(3)、在（2）的条件下，超市在获得的利润取得最大值时，决定售出的甲种蔬菜每千克捐出 $2 a$ 元，乙种蔬菜每千克捐出a元给当地福利院，若要保证捐款后的利润率不低于 $20 %$ ，求a的最大值．

查看试题解析