安徽省淮北市五校联考2021-2022学年七年级下学期期中考试数学试题

试卷更新日期：2023-03-07 类型：期中考试

进入出卷网下载

一、单选题

1. 在-22， $\sqrt{22}$ ， $- \frac{1}{22}$ ， $\sqrt[3]{22}$ 这四个数中，最小的数是（）

A、-22 B、 $\sqrt{22}$ C、 $- \frac{1}{22}$ D、 $\sqrt[3]{22}$

查看试题解析
2. 若 $(x + 4)^{0} = 1$ 成立，则x的取值范围是（）

A、x=0 B、x=4 C、 $x \neq 0$ D、 $x \neq - 4$

查看试题解析
3. 化简 $(p - q)^{6} \div (q - p)^{5}$ 的结果为（）

A、 $p - q$ B、 $q - p$ C、 $- p - q$ D、 $p + q$

查看试题解析
4. 若 $x = 1$ 是不等式 $x - y < 0$ 的一个解，则y的值不可能是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 若 $(x + 3) (x - 3) - 91 = 0$ ，则x的值为（）

A、10 B、-10 C、±10 D、9或11

查看试题解析
6. 计算 $[(3 a + b)^{2} - (3 a - b)^{2}] \div (4 a b)$ 的结果是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 下列说法中，正确的是（）

A、16的平方根是4 B、 $- 3^{2}$ 的算术平方根是3 C、1的立方根是±1 D、 $- \sqrt{3}$ 是3的一个平方根

查看试题解析
8. 有三个实数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 满足 $a_{1} - a_{2} = a_{2} - a_{3} > 0$ ，若 $a_{1} + a_{3} = 0$ ，则下列判断中正确的是（）

A、 $a_{1} < 0$ B、 $a_{2} > 0$ C、 $a_{1} + a_{2} < 0$ D、 $a_{2} \cdot a_{3} = 0$

查看试题解析
9. 若 $1 0^{a} = 20$ ， $10 0^{b} = 50$ ，则2a+b-1的值是（）

A、4 B、5 C、8 D、10

查看试题解析
10. 已知关于x的不等式组 ${\begin{array}{l} x > a \\ x < 2 \end{array}$ 的整数解共有4个，则a的取值范围是（）

A、 $- 3 < a \leq - 2$ B、 $- 3 \leq a < - 2$ C、 $- 3 < a < - 2$ D、 $a < - 2$

查看试题解析

二、填空题

11. $- \frac{2}{3}$ 的相反数是．

查看试题解析
12. 若 $(m - 2) x^{2 m - 1} - 8 > 5 m$ 是关于x的一元一次不等式，则m的值为．

查看试题解析
13. 某同学计算一个多项式乘 $- 3 x^{2}$ 时，因抄错符号，算成了加上 $- 3 x^{2}$ ，得到的答案是 $x^{2} - \frac{1}{2} x + 1$ ，那么正确的计算结果是．

查看试题解析
14.

(1)、如果一个负数的平方是36，那么这个负数是；

(2)、已知 $(x^{2} + y^{2})^{2} = 3 \frac{1}{16}$ ，那么 $x^{2} + y^{2} =$ ．

查看试题解析

三、解答题

15. 计算 $(- 1)^{- 1} + \sqrt[3]{27} - (- 2) \times \sqrt{9}$ ．

查看试题解析
16. 计算： $(- 2 x^{2})^{3} - 3 x^{4} \cdot x^{2} + 4 x^{8} \div 2 x^{2}$ ．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 5 x + 3 > 2 x \\ \frac{2 x - 1}{3} < \frac{x}{2} \end{array}$ ，并将解集在图中数轴上表示出来．

查看试题解析
18. 因式分解．

(1)、 $m (m + 6) + 9$ ；

(2)、 $(a^{2} + 1)^{2} - 4 a^{2}$ ．

查看试题解析
19. 观察如下按规律排列的数表：

第1列
第2列
第3列
第4列
第1行
$\sqrt{2 \times 0 + 1}$
第2行
$\sqrt{2 \times 1 + 1}$
$\sqrt{2 \times 1 + 2}$
第3行
$\sqrt{2 \times 2 + 1}$
$\sqrt{2 \times 2 + 2}$
$\sqrt{2 \times 2 + 3}$
第4行
$\sqrt{2 \times 3 + 1}$
$\sqrt{2 \times 3 + 2}$
$\sqrt{2 \times 3 + 3}$
$\sqrt{2 \times 3 + 4}$
…
…
…
…
…
根据该数表所反映的规律解答问题．

(1)、第5行第1列的数是（写出最后的结果）；
第n行最右边一个数是（用含n的代数式表示）；

(2)、实数 $\sqrt{66}$ 是否在这个数表中？请说明理由．

查看试题解析
20. 已知多项式 $M = x^{2} - 2 x + a$ ， $N = x + a$ ．

(1)、若在M·N的运算结果中， $x^{2}$ 的系数为-4，求a的值；

(2)、解关于x的不等式 $x^{2} - M < a N - 3 a$ ．

查看试题解析
21. 已知两个实数a，b满足 $a + b = 10$ ， $a b = 24$ ，且 $a < b$ ；分别求值；

(1)、 $a^{2} + b^{2}$ ；

(2)、 $a - b$ ；

(3)、 $2 a + 3 b$ ．

查看试题解析
22. 某制造厂决定购买A，B两种型号的污水处理设备若干台，其中每台设备的价格、月处理污水量如下表：

A型
B型
价格（万元/台）
8
6
月处理污水量（吨/月）
200
180

(1)、若要求购买资金共20万元，则该厂有哪些购买方案？

(2)、若要求购买两种设备共8台，且月处理污水量不低于1540吨，则该厂有哪些购方案？

查看试题解析
23. ［知识回顾]
有这样一类题：
代数式 $a x - y + 6 + 3 x - 5 y - 1$ 的值与x的取值无关，求a的值；
通常的解题方法；
把x，y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式 $= (a + 3) x - 6 y + 5$ ，所以 $a + 3 = 0$ ，即 $a = - 3$ ．

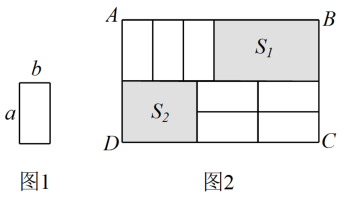(1)、［理解应用]
若关于x的多项式 $(2 m - 3) x + 2 m^{2} - 3 m$ 的值与x的取值无关，求m的值；

(2)、已知 $3 [(2 x + 1) (x - 1) - x (1 - 3 y)] + 6 (- x^{2} + x y - 1)$ 的值与x无关，求y的值；

(3)、（能力提升）如图1，小长方形纸片的长为a、宽为b，有7张图1中的纸片按照图2方式不重叠地放在大长方形ABCD内，大长方形中有两个部分（图中阴影部分）未被覆盖，设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求a与b的等量关系．

查看试题解析

	第1列	第2列	第3列	第4列
第1行	$\sqrt{2 \times 0 + 1}$
第2行	$\sqrt{2 \times 1 + 1}$	$\sqrt{2 \times 1 + 2}$
第3行	$\sqrt{2 \times 2 + 1}$	$\sqrt{2 \times 2 + 2}$	$\sqrt{2 \times 2 + 3}$
第4行	$\sqrt{2 \times 3 + 1}$	$\sqrt{2 \times 3 + 2}$	$\sqrt{2 \times 3 + 3}$	$\sqrt{2 \times 3 + 4}$
…	…	…	…	…

	A型	B型
价格（万元/台）	8	6
月处理污水量（吨/月）	200	180