吉林省长春市双阳区2022年一模考试数学试题
试卷更新日期:2023-03-07 类型:中考模拟
一、单选题
-
1. -2的绝对值是( )A、2 B、 C、 D、2. 第七次全国人口普查统计,长春市总人口约为9070000人.把“9070000”用科学记数法表示为( )A、0.907×107 B、9.07×107 C、9.07×106 D、9.07×1053. 如图是由四个相同的小正方体组成的立体图形,它的俯视图是()
 A、
A、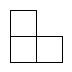 B、
B、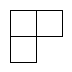 C、
C、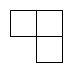 D、
D、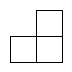 4. 一元二次方程x2-3x+1=0的根的情况为( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 一副直角三角板如图放置,点D在直线EF上,若ABEF,则∠EDC 的度数为( )
4. 一元二次方程x2-3x+1=0的根的情况为( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 一副直角三角板如图放置,点D在直线EF上,若ABEF,则∠EDC 的度数为( ) A、30° B、45° C、60° D、105°6. 如图为固定电线杆AC,在离地面高度为7米的A处引拉线AB,使拉线AB与地面BC的夹角为α,则拉线AB的长为( )
A、30° B、45° C、60° D、105°6. 如图为固定电线杆AC,在离地面高度为7米的A处引拉线AB,使拉线AB与地面BC的夹角为α,则拉线AB的长为( ) A、7sinα米 B、7cosα米 C、7tanα米 D、米7. 如图,是⊙O的切线,点A为切点,BO交⊙O于点C,BO的延长线交⊙O于点D,点E在优弧CDA上,连接AD、AE、CE,若∠BAD=122°,则∠CEA的度数为( )
A、7sinα米 B、7cosα米 C、7tanα米 D、米7. 如图,是⊙O的切线,点A为切点,BO交⊙O于点C,BO的延长线交⊙O于点D,点E在优弧CDA上,连接AD、AE、CE,若∠BAD=122°,则∠CEA的度数为( ) A、26° B、32° C、64° D、128°8. 如图,正比例函数y=mx(m>0)与反比例函数的图象交于A,B两点,轴,交y轴于点C,在射线BC上取点D,且BD=3BC,若 , 则k的值为( )
A、26° B、32° C、64° D、128°8. 如图,正比例函数y=mx(m>0)与反比例函数的图象交于A,B两点,轴,交y轴于点C,在射线BC上取点D,且BD=3BC,若 , 则k的值为( ) A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
9. 分解因式:x2﹣1= .10. 不等式组的解集是 .11. 如图,在ABC中,∠ACB=90°,分别以点A、B为圆心,大于线段AB长度一半的长为半径作弧,两弧相交于E、F两点,作直线EF,交AC于点D,点O为BD的中点,若AD=4,则OC= .
 12. 如图,在扇形中,半径的长为2,点在弧上,连接 , , , 若四边形为菱形,则图中阴影部分的面积为 . (用含的代数式表示)
12. 如图,在扇形中,半径的长为2,点在弧上,连接 , , , 若四边形为菱形,则图中阴影部分的面积为 . (用含的代数式表示) 13. 如图,将ABC绕点A顺时针旋转60°得到ADE,若∠C=50°,且AB⊥DE于点F,则∠DAE=度.
13. 如图,将ABC绕点A顺时针旋转60°得到ADE,若∠C=50°,且AB⊥DE于点F,则∠DAE=度. 14. 如图,抛物线 与y轴交于A点,与x轴交于B、C两点,B(-1,0), C(3,0),连接AC,将线段AC 向上平移落在EF处,且EF恰好经过这个抛物线的顶点D,则四边形ACFE的周长为 .
14. 如图,抛物线 与y轴交于A点,与x轴交于B、C两点,B(-1,0), C(3,0),连接AC,将线段AC 向上平移落在EF处,且EF恰好经过这个抛物线的顶点D,则四边形ACFE的周长为 .
三、解答题
-
15. 先化简,再求值: , 其中x= .16. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产480万剂疫苗所用的时间比原先生产420万剂疫苗所用的时间少1天.问原先每天生产多少万剂疫苗?17. 2022年北京冬奥会期间,小李同学手工制作了三张带有图案的不透明A、B、C卡片(其中A代表短道速滑;B代表花样滑冰;C代表速度滑冰),卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再随机抽取一张,请用画树状图(或列表)的方法,求两次抽出的卡片上的图案恰好是短道速滑和花样滑冰的概率.
 18. 在平行四边形ABCD中,CE⊥AD于点E,点F在BC 上,且BF=DE.
18. 在平行四边形ABCD中,CE⊥AD于点E,点F在BC 上,且BF=DE. (1)、求证:四边形AFCE是矩形.(2)、连接EF,若EFDC,DE=2,CE=4,则平行四边形ABCD的面积为 .19. 如图,在6×6的正方形网格中,每个小正方形的顶点称为格点,ABC的顶点均在格点上.按要求完成下列画图.(要求:用无刻度直尺,保留必要的画图痕迹,不写画法)
(1)、求证:四边形AFCE是矩形.(2)、连接EF,若EFDC,DE=2,CE=4,则平行四边形ABCD的面积为 .19. 如图,在6×6的正方形网格中,每个小正方形的顶点称为格点,ABC的顶点均在格点上.按要求完成下列画图.(要求:用无刻度直尺,保留必要的画图痕迹,不写画法) (1)、在图1中画出ABC高线CD.(2)、在图2中画出一个ABD,使 , D为格点(点D不在点C处).(3)、在图3中的BC边上找一点D,使点D到AB和AC所在的直线距离相等.20. “足球运球”是中考体育必考项目之一.某校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:80-100分,B级:70-79分,C级:60-69分,D级:10-59分),根据所给信息,解答以下问题:
(1)、在图1中画出ABC高线CD.(2)、在图2中画出一个ABD,使 , D为格点(点D不在点C处).(3)、在图3中的BC边上找一点D,使点D到AB和AC所在的直线距离相等.20. “足球运球”是中考体育必考项目之一.某校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:80-100分,B级:70-79分,C级:60-69分,D级:10-59分),根据所给信息,解答以下问题: (1)、在扇形统计图中,D对应的扇形的圆心角是度.(2)、补全条形统计图.(3)、所抽取学生的足球运球测试成绩的中位数会落在级.(4)、该校九年级有450名学生,请估计足球运球测试成绩达到A级的学生有多少人?21. 在一条笔直的公路上依次有A、C、B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息2分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
(1)、在扇形统计图中,D对应的扇形的圆心角是度.(2)、补全条形统计图.(3)、所抽取学生的足球运球测试成绩的中位数会落在级.(4)、该校九年级有450名学生,请估计足球运球测试成绩达到A级的学生有多少人?21. 在一条笔直的公路上依次有A、C、B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息2分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题: (1)、甲的骑行速度为米/分,点D的坐标为 .(2)、求甲返回时距A地的路程y与时间x之间的函数关系式(写出自变量的取值范围).(3)、甲、乙同时出发m分钟后,甲在返回过程中与乙距A地的路程相等,请直接写出m的值.22.(1)、【基础探究】如图①,在中,为上一点, , 交延长线于点 , 若 , 求的长.
(1)、甲的骑行速度为米/分,点D的坐标为 .(2)、求甲返回时距A地的路程y与时间x之间的函数关系式(写出自变量的取值范围).(3)、甲、乙同时出发m分钟后,甲在返回过程中与乙距A地的路程相等,请直接写出m的值.22.(1)、【基础探究】如图①,在中,为上一点, , 交延长线于点 , 若 , 求的长. (2)、【拓展延伸】如图②,在中,为上一点, , 交延长线于点 , , , ,则 .
(2)、【拓展延伸】如图②,在中,为上一点, , 交延长线于点 , , , ,则 . (3)、【拓展延伸】如图③,点为四边形内部一点,且有 , , 于点 , 为上一点, , 若 , , 则的面积为 .
(3)、【拓展延伸】如图③,点为四边形内部一点,且有 , , 于点 , 为上一点, , 若 , , 则的面积为 . 23. 如图,在 中,AC=AB=10, , 过点C作CD⊥AB交AB于点D,动点P、Q同时出发,点P从点A出发沿AC运动到终点C,速度为每秒5个单位长度,点Q从点B出发沿BC运动到终点C,速度为每秒个单位长度,连接PQ,过点P作PE⊥EQ,∠PQE=∠A,点E在PQ的下方,设点P运动的时间为t秒(t>0).
23. 如图,在 中,AC=AB=10, , 过点C作CD⊥AB交AB于点D,动点P、Q同时出发,点P从点A出发沿AC运动到终点C,速度为每秒5个单位长度,点Q从点B出发沿BC运动到终点C,速度为每秒个单位长度,连接PQ,过点P作PE⊥EQ,∠PQE=∠A,点E在PQ的下方,设点P运动的时间为t秒(t>0). (1)、CD= , BC= .(2)、求QE的长(用含t的代数式表示).(3)、连接DE,若DEAC,求t的值.(4)、连接BE,当BEQ的某一个内角与∠ACD互余时,直接写出t的值.24. 已知抛物线y=-x2+2mx+2(x≥2)的图象记为G1 , 抛物线y=-x2+mx(x<2)的图象记为G2 , 图象G1与图象G2合在一起记为G(m为常数).(1)、当m=1时,
(1)、CD= , BC= .(2)、求QE的长(用含t的代数式表示).(3)、连接DE,若DEAC,求t的值.(4)、连接BE,当BEQ的某一个内角与∠ACD互余时,直接写出t的值.24. 已知抛物线y=-x2+2mx+2(x≥2)的图象记为G1 , 抛物线y=-x2+mx(x<2)的图象记为G2 , 图象G1与图象G2合在一起记为G(m为常数).(1)、当m=1时,①若点P(3,n)在图象G上,则n的值为 .
②若函数值y随x的增大而增大,则x的取值范围为 .
(2)、若点Q(m,4m)在图象G上,求m的值.(3)、当图象G对应的函数最大值为2时,求m的值.(4)、图象G上有两点A和B,A点横坐标m-1,B点横坐标2-m,以AB为对角线作顶点为A、C、B、D的矩形,其中AC⊥x轴,BC⊥y轴,当与关于直线AB恰好成轴对称时,请直接写出m的值.