吉林省长春市汽开区2022年中考数学模拟试题

试卷更新日期：2023-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. －2的相反数是（）

A、2 B、－2 C、±2 D、－ $\frac{1}{2}$

查看试题解析
2. 国家统计局的相关数据显示，2019年我国国民生产总值（GDP）约为99.08万亿元，数据99.08万亿用科学记数法表示为（）

A、9.908×10¹³ B、9.908×10¹² C、99.08×10¹² D、9.908×10¹⁴

查看试题解析
3. 下列一元二次方程中，两个实数根之和为2的是（）

A、2x²+x﹣2＝0 B、x²+2x﹣2＝0 C、2x²﹣x﹣1＝0 D、x²﹣2x﹣2＝0

查看试题解析
4. 在函数 $y = \frac{k}{x} (k > 0)$ 的图象上有三点 $A_{1} (x_{1} ， y_{1})$ 、 $A_{2} (x_{2} ， y_{2})$ 、 $A_{3} (x_{3} ， y_{3})$ ，若 $x_{1} > x_{2} > 0 > x_{3}$ ，则下列各式中，正确的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
5. 如图是一个由多个相同小正方体搭成的几何体从上面看到的形状图，图中所标数字为该位置小正方体的个数，则这个几何体从正面看到的形状图是（）

A、 B、 C、 D、

查看试题解析
6. 如图，为了测得电视塔的高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进100米到达F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（）．

A、 $50 \sqrt{3}$ B、51 C、 $50 \sqrt{3} + 1$ D、101

查看试题解析
7. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，过点 $A$ 作 $⊙ O$ 的切线交对角线 $D B$ 的延长线于点 $F$ ，则下列结论不成立的是（）

A、 $A E ∥ B F$ B、 $A F ∥ C D$ C、 $D F = A F$ D、 $A B = B F$

查看试题解析
8. 如图，△ABC，∠BAC=90°，分别以点A、C为圆心，以大于 $\frac{1}{2}$ AC长为半径画弧，两弧交于点M、N，作直线MN分别交BC于D点.若AB=AD=3，则点AC的长为（）

A、6 B、8 C、2 $\sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析

二、填空题

9. 计算： $\sqrt{2} + (\sqrt{3} - \sqrt{2})$ 的结果是．

查看试题解析
10. 一个多边形截去一个角后，形成的另一个多边形的内角和是1260°，则原多边形的边数是为.

查看试题解析
11. 不等式组 ${\begin{array}{l} x + 1 > 2 \\ 3 x - 2 \leq 4 \end{array}$ 的解为．

查看试题解析
12. 扇形弧长为5πcm，面积为60πcm² ，则扇形半径为．

查看试题解析
13. 已知点 $P (a ， \frac{1}{2})$ 在二次函数 $y = 2 x^{2}$ 的图象上，则a的值等于．

查看试题解析
14. 因式分解：（a+b）²-64＝．

查看试题解析

三、解答题

15. 每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首！！！暑假将至，我校为确保学生安全，开展了“珍爱生命·谨防溺水”的防溺水安全知识竞赛，现从该校七、八年级中各随机抽取15名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示），共分为五个等级：
A． $75 \leq x < 80$ ， B． $80 \leq x < 85$ ， C． $85 < x < 90$ ， D． $90 \leq x < 95$ ， E． $95 \leq x \leq 100$ ，
下面给出了部分信息．
七年级15个学生的竞赛成绩：78，83，89，97，98，85，100，94，87，90，93，92，99，95，100
八年级15个学生的竞赛成绩中D等级包含的所有数据为：91，92，94，90，93
【七、八年级中各随机抽取15名学生的竞赛成绩统计表】
年级
平均数
众数
中位数
方差
七年级
92
$a$
93
41.7
八年级
92
87
$b$
50.2

(1)、根据以上信息，可以求出： $a =$ ， $b =$ ；

(2)、根据以上数据，你认为 ▲ 年级的学生的竞赛成绩较好，请说明理由（从两个方面分析）；

(3)、若规定评分90分及以上为优秀，若参加知识竞赛的七年级有1800人，八年级有2000人，请估算两个年级学生评分为优秀的学生共有多少个．

查看试题解析
16. 先化简，再求值： $(2 x + 1)^{2} - (2 x + 1) (2 x - 1)$ ，其中 $x = - \frac{1}{4}$ ．

查看试题解析
17. 一个不透明的口袋里有 $4$ 个除颜色外都相同的球，其中有 $3$ 个红球， $1$ 个黄球．

(1)、若从中随意摸出两个球，用树状图或列表法求摸出两个红球的概率；

(2)、若要使从中随意摸出一个球是黄球的概率为 $\frac{2}{3}$ ，求袋子中需再加入几个黄球？

查看试题解析
18. 为了响应学校提出的“节能减排，低碳生活”的倡议，班会课上小明建议每位同学都践行“双面打印，节约用纸” $.$ 他举了一个实际例子：打印一份资料，如果用 $A 4$ 厚型纸单面打印，总质量为 $400$ 克，将其全部改成双面打印，用纸将减少一半；如果用 $A 4$ 薄型纸双面打印，总质量为 $160$ 克．已知每页薄型纸比厚型纸轻 $0.8$ 克，求例子中的 $A 4$ 厚型纸每页的质量． $($ 墨的质量忽略不计 $)$ 提示：总质量 $=$ 每页纸的质量 $\times$ 纸张数．

查看试题解析
19. 容积为800立方米的水池内已贮水200立方米，若每分钟注入的水量是15立方米，设池内的水量为Q(立方米)，注水时间为t(分)．

(1)、请写出Q与t之间的函数关系式．

(2)、注水多长时间可以把水池注满?

(3)、当注水时间为0.2小时时，池中的水量是多少?

查看试题解析
20. 先画出 $△ A B C$ 关于直线 $l_{1}$ 对称的图形 $△ A_{1} B_{1} C_{1}$ ，再画出 $△ A_{1} B_{1} C_{1}$ 关于直线 $l_{2}$ 对称的图形 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
21. 角的平分线的判定定理：角的内部到角的两边的距离相等的点在角的平分线上．
小强证明该定理的步骤如下：
已知：如图1，点P在 $O C$ 上， $P D ⊥ O A$ 于点D， $P E ⊥ O B$ 于点E，且 $P D = P E$ ．
求证： $O C$ 是 $∠ A O B$ 的平分线．
证明：通过测量可得 $∠ A O C = 23 °$ ， $∠ B O C = 23 °$ ．
∴ $∠ A O C = ∠ B O C$ ． ∴ $O C$ 是 $∠ A O B$ 的平分线．

(1)、关于定理的证明，下面说法正确的是（）

A、小强用到了从特殊到一般的方法证明该定理． B、只要测量一百个到角的两边的距离相等的点都在角的平分线上，就能证明该定理． C、不能只用这个角，还需要用其它角度进行测量验证，该定理的证明才完整． D、小强的方法可以用作猜想，但不属于严谨的推理证明．

(2)、利用小强的已知和求证，请你证明该定理；

(3)、如图2，在五边形 $A B C D E$ 中， $B C = C D = D E$ ， $∠ A B C = 80 °$ ， $∠ B A E = 110 °$ ， $∠ A E D = 100 °$ ，在五边形 $A B C D E$ 内有一点F，使得 $S_{△ B C F} = S_{△ C D F} = S_{△ D E F}$ ．直接写出 $∠ C F D$ 的度数．

查看试题解析
22. 如图，在边长为8的正方形ABCD中，E是AB上的点，⊙O是以BC为直径的圆．

(1)、如图1，若DE与⊙O相切于点F，求BE的长；

(2)、如图2，若AO⊥DE，垂足为F，求EF的长．

查看试题解析
23. 【问题情境】在综合与实践课上，老师让同学们以“平行四边形的剪拼”为主题开展数学活动，如图1，在平行四边形纸片ABCD中， $B A = B C$ ，沿该纸片对角线AC剪开，得到 $△ B A C$ 和 $△ D A C$ ．

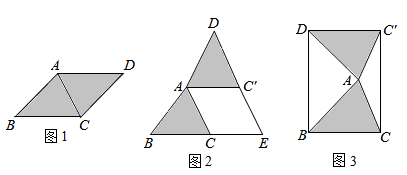(1)、【操作发现】将图1中的 $△ A C D$ 以A为旋转中心，逆时针方向旋转角 $α$ ，使 $α = ∠ B A C$ ，得到如图2所示的 $△ A C^{'} D$ ，分别延长BC和 $D C^{'}$ 交于点E，请判四边形 $A C E C^{^{'}}$ 的形状，并说明理由．

(2)、创新小组将图1中的 $△ A C D$ 以A为旋转中心，按逆时针方向旋转角 $α$ ，得到如图3所示的平行四边形 $B C C^{'} D$ ，且 $∠ B C C^{'} = 90 °$ ，请判断此时 $α$ 与 $∠ B A C$ 的数量关系．并说明理由；

(3)、【实践探究】缜密小组在创新小组发现结论的基础上，量得图3中 $B C = 13$ cm， $A C = 10$ cm，请直接写出BD的长．

查看试题解析
24. 已知抛物线 $y = x^{2} + (m + 1) x + m$ ．

(1)、无论m取何值，该抛物线总经过一定点，定点坐标为．

(2)、抛物线与直线y＝x＋1交于两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，且 $x_{1} < x_{2}$ ，若 $x_{1} + x_{2} = 3$ ，求m的值．

(3)、点P是抛物线上第四象限内一动点，在（2）的条件下，求△PAB面积的最大值．

查看试题解析

年级	平均数	众数	中位数	方差
七年级	92	$a$	93	41.7
八年级	92	87	$b$	50.2