吉林省松原市乾安县2022年中考模拟数学试题
试卷更新日期:2023-03-07 类型:中考模拟
一、单选题
-
1. 2022的相反数是( )A、2022 B、 C、 D、2. 2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组三位航天员进行授课,央视新闻抖音号进行全程直播,某一时刻观看人数达到379.2万,数字379.2万用科学记数法可以表示为( )A、 B、 C、 D、3. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列说法正确的是( ).
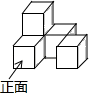 A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是44. 下列运算中,正确的是( )A、x2+2x2=3x4 B、x2·x3=x6 C、(x2)3=x6 D、(xy)3=xy35. 如图,正五边形ABCDE内接于⊙O,P为弧DE上的一点(点P不与点D重合),则∠CPD等于( )
A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是44. 下列运算中,正确的是( )A、x2+2x2=3x4 B、x2·x3=x6 C、(x2)3=x6 D、(xy)3=xy35. 如图,正五边形ABCDE内接于⊙O,P为弧DE上的一点(点P不与点D重合),则∠CPD等于( ) A、36° B、40° C、60° D、72°6. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只 雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )A、 B、 C、 D、
A、36° B、40° C、60° D、72°6. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只 雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )A、 B、 C、 D、二、填空题
-
7. 因式分解mn-m= .8. 不等式3x-1>5的解集是 .9. 若关于x的一元二次方程有两个不相等的实数根,则k的值可以是(写出一个即可).10. 将一张等宽的直条型纸片按图中方式折叠,若∠1 = 50°, 则∠2的度数为 .
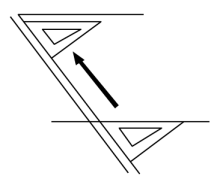
 11. 如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是。
11. 如图,给出了直线外一点作已知直线平行线的一种方法,它的依据是。
 12. 如图,在平面直角坐标系中,直线交轴于A,B两点,将线段AB绕点B逆时针旋转 , 点A落在处,则点的坐标为 .
12. 如图,在平面直角坐标系中,直线交轴于A,B两点,将线段AB绕点B逆时针旋转 , 点A落在处,则点的坐标为 . 13. 用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压cm.
13. 用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压cm. 14. 如图,在扇形AOB中 ,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为 时,则阴影部分的面积为 .
14. 如图,在扇形AOB中 ,正方形CDEF的顶点C是 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为 时,则阴影部分的面积为 .
三、解答题
-
15. 以下是小鹏化简代数式的过程.
 (1)、小鹏的化简过程在第步开始出错,错误的原因是 .(2)、请你帮助小鹏写出正确的化简过程,并计算当时代数式的值.16. 为了尽快实现长春市新冠病毒感染者动态清零的目标,社区招募志愿者参加核酸检测工作,小明和小红在同一个小区居住,他们同时报名当本小区的志愿者.小区内共分成1,2,3三个核酸检测小组(他们被分到每个小组的机会是均等的).(1)、小红被分到2组的概率是 .(2)、用列表或者画树状图的方法,求小明和小红被分到一个小组的概率.17. 2022年北京冬奥会期间吉祥物冰墩墩受到了很多人的喜欢,一墩难求.某生产厂接到了要求几天内生产出14400个冰墩墩外套的加工任务,为了让更多人尽快拿到冰墩墩,工人们愿意奉献自己的休息时间来完成这项任务,厂长决定开足全厂生产线进行生产,实际每天加工的个数比原计划多 , 结果提前4天完成任务.问实际每天加工多少个冰墩墩外套?18. 如图,在 和 中,AC与BD相交于点E,AD=BC,AC=BD.求证:∠C=∠D.
(1)、小鹏的化简过程在第步开始出错,错误的原因是 .(2)、请你帮助小鹏写出正确的化简过程,并计算当时代数式的值.16. 为了尽快实现长春市新冠病毒感染者动态清零的目标,社区招募志愿者参加核酸检测工作,小明和小红在同一个小区居住,他们同时报名当本小区的志愿者.小区内共分成1,2,3三个核酸检测小组(他们被分到每个小组的机会是均等的).(1)、小红被分到2组的概率是 .(2)、用列表或者画树状图的方法,求小明和小红被分到一个小组的概率.17. 2022年北京冬奥会期间吉祥物冰墩墩受到了很多人的喜欢,一墩难求.某生产厂接到了要求几天内生产出14400个冰墩墩外套的加工任务,为了让更多人尽快拿到冰墩墩,工人们愿意奉献自己的休息时间来完成这项任务,厂长决定开足全厂生产线进行生产,实际每天加工的个数比原计划多 , 结果提前4天完成任务.问实际每天加工多少个冰墩墩外套?18. 如图,在 和 中,AC与BD相交于点E,AD=BC,AC=BD.求证:∠C=∠D. 19. 如图是的小正方形网格,的顶点都在格点上.
19. 如图是的小正方形网格,的顶点都在格点上.按下列要求作图(所画的顶点都在格点上,并标注对应字母);
(1)、在图1中,画出 , 使与关于直线成轴对称; (2)、在图2中,将绕某一格点旋转得到 , 使与成中心对称,画出 , 并在图中标出旋转中心 .
(2)、在图2中,将绕某一格点旋转得到 , 使与成中心对称,画出 , 并在图中标出旋转中心 . 20. 如图,点和点B在反比例函数的图像上,轴于点D,轴于点C,轴于点E,交于点F.
20. 如图,点和点B在反比例函数的图像上,轴于点D,轴于点C,轴于点E,交于点F. (1)、求反比例函数的解析式.(2)、若 , 求四边形的面积.21. 如图1是一辆吊车的实物图,图2是其工作示意图,其转动点 离地面 的高度 为 是可以伸缩的起重臂,当 长度为 ,张角 为 时,求起重臂顶点 离地面 的高度(结果保留小数点后一位).(参考数据: )
(1)、求反比例函数的解析式.(2)、若 , 求四边形的面积.21. 如图1是一辆吊车的实物图,图2是其工作示意图,其转动点 离地面 的高度 为 是可以伸缩的起重臂,当 长度为 ,张角 为 时,求起重臂顶点 离地面 的高度(结果保留小数点后一位).(参考数据: ) 22. 为了调查八年级学生网课期间体育锻炼的时间情况,某校在八年级 名学生中随机抽取了男生,女生各 名,收集得到了以下数据: (单位: 分钟)
22. 为了调查八年级学生网课期间体育锻炼的时间情况,某校在八年级 名学生中随机抽取了男生,女生各 名,收集得到了以下数据: (单位: 分钟)女生: .
男生: , .
整理数据:制作了如下统计表,

分析数据:两组数据的平均数、中位数、众数如表所示,
 (1)、请将上面的表格补充完整: , , , ;(2)、若该校学生 为男生,根据调查的数据,估计八年级居家体育锻炼的时间在 分钟以上(不包含 分钟)的男生的有多少名?(3)、体育老师分析表格数据后,认为八年级的男生居家体育锻炼做得比女生好,请你结合统计数据,写出一条同意体育老师观点的理由.23. 李师傅驾车从甲地到乙地,途中在加油站加了一次油,加油时,车载电脑显示油箱中剩余油量4升,已知汽车行驶时,每小时耗油量一定,设油箱中剩余油量为(升),汽车行驶时间为(时),与之间的函数图象如图所示.
(1)、请将上面的表格补充完整: , , , ;(2)、若该校学生 为男生,根据调查的数据,估计八年级居家体育锻炼的时间在 分钟以上(不包含 分钟)的男生的有多少名?(3)、体育老师分析表格数据后,认为八年级的男生居家体育锻炼做得比女生好,请你结合统计数据,写出一条同意体育老师观点的理由.23. 李师傅驾车从甲地到乙地,途中在加油站加了一次油,加油时,车载电脑显示油箱中剩余油量4升,已知汽车行驶时,每小时耗油量一定,设油箱中剩余油量为(升),汽车行驶时间为(时),与之间的函数图象如图所示. (1)、求李师傅加油前与之间的函数关系式;(2)、求的值;(3)、李师傅在加油站的加油量.24. 如图1,在等腰中,为中线,将线段绕点逆时针旋转;得到线段连接交直线于点 , 连接 .
(1)、求李师傅加油前与之间的函数关系式;(2)、求的值;(3)、李师傅在加油站的加油量.24. 如图1,在等腰中,为中线,将线段绕点逆时针旋转;得到线段连接交直线于点 , 连接 . (1)、若 , 则 ;(2)、若是钝角时,
(1)、若 , 则 ;(2)、若是钝角时,①请在图2中依题意补全图形,并标出对应字母;
②探究图2中的形状,并说明理由;
③若则 ▲ .
25. 如图,在RtABC中,∠ACB=90°,AC=6,BC=8,CD为斜边AB的中线.点P从点A出发,沿AB以每秒5个单位的速度向终点B运动.过点P作PE⊥AC于E,PF⊥BC于F,得到矩形PECF,CD与矩形PECF的一边交于点G,连接PC.设点P的运动时间为t秒. (1)、求线段CF的长(用含t的代数式表示);(2)、当时,求线段PG的长;(3)、当点P不与点A、B、D重合时,设矩形PECF与PCD重叠部分图形的面积为S,求S与t之间的函数关系式.26. 如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)、求点B的坐标;(2)、求经过A、O、B三点的抛物线的解析式;(3)、在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)、如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
(1)、求线段CF的长(用含t的代数式表示);(2)、当时,求线段PG的长;(3)、当点P不与点A、B、D重合时,设矩形PECF与PCD重叠部分图形的面积为S,求S与t之间的函数关系式.26. 如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)、求点B的坐标;(2)、求经过A、O、B三点的抛物线的解析式;(3)、在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)、如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.