吉林省四平市双辽市2022年中考一模数学试题
试卷更新日期:2023-03-07 类型:中考模拟
一、单选题
-
1. 2的相反数是( )A、2 B、-2 C、 D、2. 如图所示三棱柱的主视图是( )
 A、
A、 B、
B、 C、
C、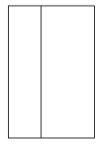 D、
D、 3. 计算的结果( )A、 B、 C、 D、4. 不等式的解集是( )A、 B、 C、 D、5. 如图,在△ABC中,∠A=46°,∠B=72°.若直线l∥BC,则∠1的度数为( )
3. 计算的结果( )A、 B、 C、 D、4. 不等式的解集是( )A、 B、 C、 D、5. 如图,在△ABC中,∠A=46°,∠B=72°.若直线l∥BC,则∠1的度数为( )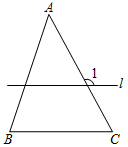 A、117° B、120° C、118° D、128°6. 如图,AB是⊙O的直径,点C是⊙O上一点,若∠BAC=30°,BC=2,则AB的长为( ).
A、117° B、120° C、118° D、128°6. 如图,AB是⊙O的直径,点C是⊙O上一点,若∠BAC=30°,BC=2,则AB的长为( ). A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
7. 计算:= .8. 因式分解:a2+2a+1= .9. 若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为 .10. 一元二次方程 的解是.11. 如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条直的参照线,这样做的依据是 .
 12. 如图,直线 , 直线交 , , 于点 , , ;直线交 , , 于点 , , .已知 , 则 .
12. 如图,直线 , 直线交 , , 于点 , , ;直线交 , , 于点 , , .已知 , 则 . 13. 如图,四边形是平行四边形,以点B为圆心,的长为半径作弧交于点E,分别以点C,E为圆心、大于的长为半径作弧,两弧交于点P,作射线交的延长线于点F, , 则的长为 .
13. 如图,四边形是平行四边形,以点B为圆心,的长为半径作弧交于点E,分别以点C,E为圆心、大于的长为半径作弧,两弧交于点P,作射线交的延长线于点F, , 则的长为 . 14. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8.若E、F是BC边上的两个动点,以EF为边的等边△EFP的顶点P在△ABC内部或边上,则等边△EFP的周长的最大值为 .
14. 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8.若E、F是BC边上的两个动点,以EF为边的等边△EFP的顶点P在△ABC内部或边上,则等边△EFP的周长的最大值为 .
三、解答题
-
15. 先化简,再求值: , 其中 .16. 在一个不透明的布袋里装有4个球,其中1个红球,1个黄球,2个白球,它们除颜色外其余都相同.(1)、若从中任意摸出一个球,求摸出白球的概率;(2)、若摸出1个球,记下颜色后不放回,再摸出1个球,求两次摸出的球恰好一黄一白的概率(要求画树状图或列表).17. 《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问物价几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问这个物品的价格是多少元?18. 如图,在△ABC中,点D是BC的中点,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.求证:△BDE≌△CDF.
 19. 图①、图②均为的正方形网格,点A、B、C在格点上.
19. 图①、图②均为的正方形网格,点A、B、C在格点上.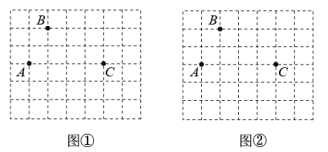
( 1 )在图①中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为轴对称图形.(画一个即可)
( 2 )在图②中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为中心对称图形.(画一个即可)
20. 如图所示是自动卸货汽车卸货的状态图和其示意图,汽车的车厢采用液压机构,车厢的支撑顶杆AB的底部支撑点B在水平线OP的下方,OB与水平线OP夹角是15°,卸货时车厢与水平线OP成40°,此时OB与支持顶杆AB的夹角为45°,若OA=3米,求AB的长度.(精确到十分位,sin80°≈0.9848,cos80°≈0.1736,tan80°≈5.6712)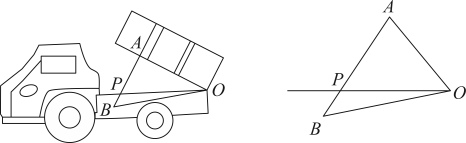 21. 如图,已知点A是一次函数的图象与x轴的交点,将点A向上平移2个单位后所得点B在某反比例函数图象上.
21. 如图,已知点A是一次函数的图象与x轴的交点,将点A向上平移2个单位后所得点B在某反比例函数图象上. (1)、求点A的坐标;(2)、确定该反比例函数的表达式.22. 促进青少年健康成长是实施“健康中国”战略的重要内容,为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,据统计,所有学生一分钟的跳绳数不少于10次,现随机抽取了部分学生一分钟跳绳的次数进行调查统计,并根据成绩分布情况,将抽取的全部成绩分成A、B、C、D四组,并绘制了如下统计图表:
(1)、求点A的坐标;(2)、确定该反比例函数的表达式.22. 促进青少年健康成长是实施“健康中国”战略的重要内容,为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,据统计,所有学生一分钟的跳绳数不少于10次,现随机抽取了部分学生一分钟跳绳的次数进行调查统计,并根据成绩分布情况,将抽取的全部成绩分成A、B、C、D四组,并绘制了如下统计图表:等级
次数
频数
A
4
B
12
C
14
D
m
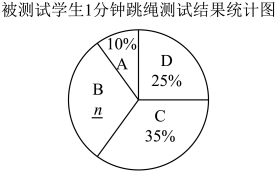
请结合上述信息完成下列问题:
(1)、 , ;(2)、上述样本数据的中位数落在组;(3)、若A组学生一分钟跳绳的平均次数为110次,B组学生一分钟跳绳的平均次数为130次,C组学生一分钟跳绳的平均次数为150次,D组学生一分钟跳绳的平均次数为190次,请你估计该校学生一分钟跳绳的平均次数是多少?23. 甲同学骑共享单车保持匀速从家到公园,到达公园后休息了一会,以相同的速度原路骑共享单车返回家中,设甲同学距离家的路程为y(m),运动时间为x(min),y与x之间的函数图象如图所示.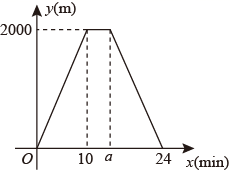 (1)、a= .(2)、在甲同学从公园返回家的过程中,求y与x之间的函数关系式.(3)、在甲同学从家出发的同时,乙同学以100m/min的速度从公园匀速步行去甲同学家学习,当乙同学与甲同学之间的路程为200m时,直接写出甲同学的运动时间.24. 如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)、a= .(2)、在甲同学从公园返回家的过程中,求y与x之间的函数关系式.(3)、在甲同学从家出发的同时,乙同学以100m/min的速度从公园匀速步行去甲同学家学习,当乙同学与甲同学之间的路程为200m时,直接写出甲同学的运动时间.24. 如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.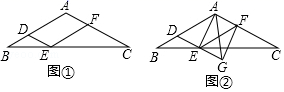 (1)、求证:四边形ADEF为平行四边形;(2)、当点D为AB中点时,判断▱ADEF的形状;(3)、延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.25. 如图,在中, . 点P从点A出发,沿折线以每秒5个单位长度的速度向点C运动,同时点D从点C出发,沿以每秒2个单位长度的速度向点A运动,点P到达点C时,点P、D同时停止运动.当点P不与点A,C重合时,作点P关于直线的对称点Q,连接交于点E,连接 . 设点P的运动时间为t秒.
(1)、求证:四边形ADEF为平行四边形;(2)、当点D为AB中点时,判断▱ADEF的形状;(3)、延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.25. 如图,在中, . 点P从点A出发,沿折线以每秒5个单位长度的速度向点C运动,同时点D从点C出发,沿以每秒2个单位长度的速度向点A运动,点P到达点C时,点P、D同时停止运动.当点P不与点A,C重合时,作点P关于直线的对称点Q,连接交于点E,连接 . 设点P的运动时间为t秒. (1)、当点P与点B重合时,求t的值;(2)、用含t的代数式表示线段的长;(3)、当为等腰直角三角形时,求t的值.26. 如图.在平面直角坐标系中,已如抛物线与x轴交于两点,与y轴交于点 .
(1)、当点P与点B重合时,求t的值;(2)、用含t的代数式表示线段的长;(3)、当为等腰直角三角形时,求t的值.26. 如图.在平面直角坐标系中,已如抛物线与x轴交于两点,与y轴交于点 . (1)、求抛物线的解析式;(2)、在抛物线上是否存在点P,使得是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标:若不存在,请说明理由;(3)、点G为抛物线上的一动点,过点G作垂直于y轴于点E,交直线于点D,过点D作x轴的垂线垂足为点F,连接 , 当线段的长度最短时,求出点G的坐标.
(1)、求抛物线的解析式;(2)、在抛物线上是否存在点P,使得是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标:若不存在,请说明理由;(3)、点G为抛物线上的一动点,过点G作垂直于y轴于点E,交直线于点D,过点D作x轴的垂线垂足为点F,连接 , 当线段的长度最短时,求出点G的坐标.