吉林省四平市双辽市2022年中考二模数学试题

试卷更新日期：2023-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $3 \times (- 2)$ 的结果是（）

A、 $- 6$ B、 $- 5$ C、 $1$ D、 $6$

查看试题解析
2. 截止2021年4月17日，全国接种新冠病毒疫苗达到 $1.898 × 1 0^{8}$ 剂次，则数据 $1.898 × 1 0^{8}$ 表示的原数是（）

A、1898000 B、18980000 C、189800000 D、1898000000

查看试题解析
3. 下列图形中不是正方体的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，直线a、b被直线c所截．若∠1=55°，则∠2的度数是（）时能判定a∥b．

A、35° B、45° C、125° D、145°

查看试题解析
5. 用代数式表示：a与3的差的2倍.下列表示正确的是（）

A、2a﹣3 B、2a＋3 C、2（a﹣3） D、2（a＋3）

查看试题解析
6. 如图，A、B是⊙O上的两点，∠AOB＝120°，OA＝3，则劣弧AB的长是（）

A、π B、2π C、3π D、4π

查看试题解析

二、填空题

7. 计算： $\sqrt{8}$ =

查看试题解析
8. 分解因式 $m^{2} + 6 m =$ .

查看试题解析
9. 若关于x的一元二次方程 $3 x^{2} - 2 x - k = 0$ 有两个相等的实数根，则k的值为．

查看试题解析
10. 分式方程 $\frac{3}{x - 2} = 1$ 的解是 $x =$ .

查看试题解析
11. 如图，在 $△ A B C$ 中， $A C = 6 ， B C = 3$ ，分别以点A，B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M，N，作直线 $M N$ 交 $A C$ 于点D，连接 $B D$ ，则 $△ B C D$ 的周长为．

查看试题解析
12. 如图，已知在 $△ A B C$ 中， $A B = 6$ ． $A C = 10$ ， $D$ ， $E$ 分别是 $A B$ ， $A C$ 的中点，连接 $D E$ ．若 $D E = 4$ ，则 $△ A B C$ 的面积是．

查看试题解析
13. 如图，直线l的函数表达式为 $y = x - 1$ ，在直线l上顺次取点 $A_{1} (2 ， 1) ， A_{2} (3 ， 2) ， A_{3} (4 ， 3) ， A_{4} (5 ， 4) ， \cdot \cdot \cdot ， A_{n} (n + 1 ， n)$ ，构成形如“┐”的图形的阴影部分面积分别表示为 $S_{1} ， S_{2} ， S_{3} ， \cdot \cdot \cdot ， S_{n}$ ，则 $S_{2022} =$ ．

查看试题解析
14. 如图，正方形纸片ABCD的边长为12，点F是AD上一点，将 $△ C D F$ 沿CF折叠，点D落在点G处，连接DG并延长交AB于点E ．若 $A E = 5$ ，则GE的长为．

查看试题解析

三、解答题

15. 先化简，再求值： $(a + 3)^{2} - 2 (3 a + 4)$ ，其中 $a = - 2$ ．

查看试题解析
16. 泰州的旅游景点很多，现有A、B、C三个景点.

(1)、若小明任选一个景点游玩，问选中A景点的概率是多少？

(2)、若小明任选两个景点游玩，问选中A和B两个景点的概率是多少？（用列表法或树状图求解）

查看试题解析
17. 为迎接母亲节，某花店老板决定将玫瑰花每枝降价1元促销，降价后，30元可购买玫瑰花的数量是原来可购买玫瑰花数量的1.5倍．求降价后每枝玫瑰花的售价．

查看试题解析
18. 如图，点A、B、D、E在同一条直线上， $A B = D E ， A C // D F ， B C // E F$ .求证： $△ A B C ≌ △ D E F$ .

查看试题解析
19. 如图，在由边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
（ 1 ）画出△ABC关于点C成中心对称的△A'B'C（其中A'是点A的对应点，B'是点B的对应点）；
（ 2 ）用无刻度的直尺作出一个格点O，使得OA=OB．

查看试题解析
20. 2021年3月23日，中国台湾的超大型集装箱船“长赐号”在经过苏伊士运河时为发生搁浅事故，造成超过400多艘货船滞留，对埃及和全球贸易造成巨大损失“长赐号”船身呈长方形，如图所示，长BC＝400米，宽CD＝60米，船身和河岸的夹角∠BCP＝30°．河岸MN//PQ，求河岸MN与PQ之间的距离（结果保留根号）．

查看试题解析
21. 如图，在平面直角坐标系中，点O为原点，反比例函数 $y = \frac{k}{x}$ 的图象经过点（1，6），菱形OABC的顶点A在函数的图象上，对角线OB在x轴上．

(1)、求反比例函数的关系式；

(2)、求菱形OABC的面积．

查看试题解析
22. 第24届冬奥会于2022年2月在北京举行，为推广冰雪运动，发挥冰雪项目的育人功能，教育部近年启动了全国冰雪运动特色学校的䢯选工作．某中学通过将冰雪运动 “早地化” 的方式积极开展了基础滑冰、早地滑雪、早地冰球、早地冰显四个运动项目，要求每一位学生都自主选择一个运动项目，为了了解学生选择冰雪运动项目的情况，随机抽取了部分学生进行调查，并根据调查结果绘制成如下不完整的条形统计图和扇形统计图．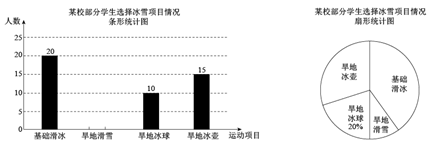

(1)、这次随机抽取了 ▲ 名学生进行调查，并将条形统计图补充完整．

(2)、求扇形统计图中 “旱地冰壶” 部分的圆心角度数．

(3)、如果该校共有2400名学生，请你估计全校学生中喜欢基础滑冰项目有多少人?

查看试题解析
23. 如图①是甲，乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形实心铁块立放其中（圆柱形实心铁块的下底面完全落在乙槽底面上），现将甲槽中的水匀速注入乙槽，甲，乙两个水槽中水的深度 $y (c m)$ 与注水时间 $x (m i n)$ 之间的关系如图②所示，根据图像解答下列问题：

(1)、图②中折线 $E D C$ 表示槽中水的深度与注入时间之间的关系；线段 $A B$ 表示槽中水的深度与注入时间之间的关系；铁块的高度为cm．

(2)、注入多长时间，甲､乙两个水槽中水的深度相同？（请写出必要的计算过程）

查看试题解析
24. 【阅读理解】如图1， $l_{1} / / l_{2}$ ， $△ A B C$ 的面积与 $△ D B C$ 的面积相等吗？为什么？
解：相等，在 $△ A B C$ 和 $△ D B C$ 中，分别作 $A E ⊥ l_{2}$ ， $D F ⊥ l_{2}$ ，垂足分别为 $E$ ， $F$ ．
$∴ ∠ A E F = ∠ D F C = 90 °$ ，
$∴ A E / / D F$ ．
$∵ l_{1} / / l_{2}$ ，
$∴$ 四边形 $A E F D$ 是平行四边形，
$∴ A E = D F$ ．
又 $S_{△ A B C} = \frac{1}{2} B C \cdot A E$ ， $S_{△ D B C} = \frac{1}{2} B C \cdot D F$ ，
$∴ S_{△ A B C} = S_{△ D B C}$ ．

(1)、【类比探究】问题①，如图2，在正方形 $A B C D$ 的右侧作等腰 $△ C D E$ ， $C E = D E$ ， $A D = 4$ ，连接 $A E$ ，求 $△ A D E$ 的面积．
解：过点 $E$ 作 $E F ⊥ C D$ 于点 $F$ ，连接 $A F$ ．
请将余下的求解步骤补充完整．

(2)、【拓展应用】问题②，如图3，在正方形 $A B C D$ 的右侧作正方形 $C E F G$ ，点 $B$ ， $C$ ， $E$ 在同一直线上， $A D = 4$ ，连接 $B D$ ， $B F$ ， $D F$ ，直接写出 $△ B D F$ 的面积．

查看试题解析
25. 在平面直角坐标系中，O为原点， $△ O A B$ 是等腰直角三角形， $∠ O B A = 90 ° ， B O = B A$ ，顶点 $A (4 ， 0)$ ，点B在第一象限，矩形 $O C D E$ 的顶点 $E (- \frac{7}{2} ， 0)$ ，点C在y轴的正半轴上，点D在第二象限，射线 $D C$ 经过点B．

(1)、如图①，求点B的坐标；

(2)、将矩形 $O C D E$ 沿x轴向右平移，得到矩形 $O^{'} C^{'} D^{'} E^{'}$ ，点O，C，D，E的对应点分别为 $O^{'}$ ， $C^{'}$ ， $D^{'}$ ， $E^{'}$ ，设 $O O^{'} = t$ ，矩形 $O^{'} C^{'} D^{'} E^{'}$ 与 $△ O A B$ 重叠部分的面积为S．
①如图②，当点 $E^{'}$ 在x轴正半轴上，且矩形 $O^{'} C^{'} D^{'} E^{'}$ 与 $△ O A B$ 重叠部分为四边形时， $D^{'} E^{'}$ 与 $O B$ 相交于点F，试用含有t的式子表示S，并直接写出t的取值范围；
②当 $\frac{5}{2} \leq t \leq \frac{9}{2}$ 时，求S的取值范围（直接写出结果即可）．

查看试题解析
26. 如图，在平面直角坐标系中，四边形ABCD为正方形，点A，B在 $x$ 轴上，抛物线 $y = x^{2} + b x + c$ 经过点B， $D (- 4 ， 5)$ 两点，且与直线DC交于一点E．

(1)、求抛物线的解析式；

(2)、若点P为y轴上一点，探究 $E P + P B$ 是否存在最小值．若存在，请求出这个最小值及点P的坐标；若不存在，请说明理由；

(3)、若点F为抛物线对称轴上一点，点Q为平面直角坐标系中的一点，是否存在以点Q，F，E，B为顶点的四边形是以BE为边的菱形．若存在，请求出点F的坐标；若不存在，请说明理由；

查看试题解析