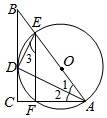广东省湛江市经济开发区2022年中考模拟数学试题
试卷更新日期:2023-03-07 类型:中考模拟
一、单选题
-
1. 若点 与点 关于原点成中心对称,则 的值是( )A、1 B、3 C、5 D、72. 一元二次方程配方后可变形为( )A、 B、 C、 D、3. 下列对二次函数y=x2﹣x的图象的描述,正确的是( )A、开口向下 B、对称轴是y轴 C、经过原点 D、在对称轴右侧部分是下降的4. 如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
 A、sinA= B、cosA= C、tanA= D、tanB=5. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、 C、 D、6. 已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+1的值为( )A、0 B、1 C、 D、27. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A、sinA= B、cosA= C、tanA= D、tanB=5. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、 C、 D、6. 已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+1的值为( )A、0 B、1 C、 D、27. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )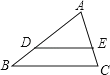 A、1 B、2 C、3 D、48. 如图,从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )
A、1 B、2 C、3 D、48. 如图,从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是( )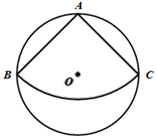 A、 B、 C、 D、19. 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=55°,则∠COD的大小为( )
A、 B、 C、 D、19. 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=55°,则∠COD的大小为( ) A、70° B、60° C、55° D、35°10. 如图,已知E是正方形ABCD中AB边延长线上一点,且AB=BE,连接CE、DE,DE与BC交于点N,F是CE的中点,连接AF交BC于点M,连接BF.有如下结论:①DN=EN;②△ABF~△ECD;③tan∠CDE=;④ , 其中正确的是( )
A、70° B、60° C、55° D、35°10. 如图,已知E是正方形ABCD中AB边延长线上一点,且AB=BE,连接CE、DE,DE与BC交于点N,F是CE的中点,连接AF交BC于点M,连接BF.有如下结论:①DN=EN;②△ABF~△ECD;③tan∠CDE=;④ , 其中正确的是( ) A、①②③④ B、①②③ C、①③④ D、①②④
A、①②③④ B、①②③ C、①③④ D、①②④二、填空题
-
11. 在平面直角坐标系中, 三个顶点的坐标分别为 .以原点 为位似中心,把这个三角形缩小为原来的 ,得到 ,则点 的对应点 的坐标是 .12. 计算6sin45°-2cos60°= .13. 将抛物线y=﹣2x2+5向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为.14. 如果 , 那么 .15. 在中,分别为的中点.若 , 则 .16. 如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△ABC绕A点逆时针旋转70°得到△ADE,连接EC,则tan∠DEC的值是 .
 17. 如图,在平面直角坐标系中,点A在y轴的正半轴上,OA=1,将OA绕点O顺时针旋转45°到OA1 , 扫过的面积记为S1 , A1A2⊥OA1交x轴于点A2;将OA2绕点O顺时针旋转45°到OA3 , 扫过的面积记为S2 , A3A4⊥OA3交y轴于点A4;将OA4绕点O顺时针旋转45°到OA5 , 扫过的面积记为S3;…;按此规律,则S2021为 .
17. 如图,在平面直角坐标系中,点A在y轴的正半轴上,OA=1,将OA绕点O顺时针旋转45°到OA1 , 扫过的面积记为S1 , A1A2⊥OA1交x轴于点A2;将OA2绕点O顺时针旋转45°到OA3 , 扫过的面积记为S2 , A3A4⊥OA3交y轴于点A4;将OA4绕点O顺时针旋转45°到OA5 , 扫过的面积记为S3;…;按此规律,则S2021为 .
三、解答题
-
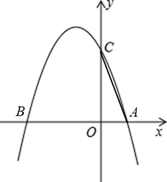
18. 用适当的方法解方程:x2-3x-4=019. 如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点.
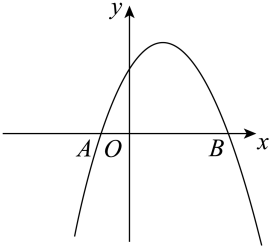 (1)、求抛物线的解析式和顶点坐标;(2)、当0<x<3时,直接写出y的取值范围;20. 如图,在ABC中,点D在BC上, .
(1)、求抛物线的解析式和顶点坐标;(2)、当0<x<3时,直接写出y的取值范围;20. 如图,在ABC中,点D在BC上, . (1)、求证:;(2)、当∠B=40°时,求∠ACE的大小.21. 如图,⊙O为锐角△ABC的外接圆,半径为5.
(1)、求证:;(2)、当∠B=40°时,求∠ACE的大小.21. 如图,⊙O为锐角△ABC的外接圆,半径为5. (1)、用尺规作图作出∠BAC的平分线,并标出它与劣弧的交点E(保留作图痕迹,不写作法);(2)、若(1)中的点E到弦BC的距离为3,求BC的长.22. 已知关于 的一元二次方程 .(1)、求证:无论 为任何实数,此方程总有两个实数根;(2)、若方程的两个实数根为 、 ,满足 ,求 的值;(3)、若 △ 的斜边为5,另外两条边的长恰好是方程的两个根 、 ,求 的内切圆半径.23. 2022年2月4日,第24届冬季奥林匹克运动会将在北京举行,吉祥物“冰墩墩”备受人民的喜爱. 某商店经销一种吉祥物玩具,销售成本为每件40元,据市场分析,若按每件80元销售,一个月能售出100件;销售单价每降1元,月销售量就增加5件,针对这种玩具的销售情况,请解答以下问题:(1)、设每件玩具的售价为x元(x为正整数),每月的销售量为y件.直接写出y与x的函数关系式;(2)、设该商店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该商店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定吉祥物玩具的销售单价?
(1)、用尺规作图作出∠BAC的平分线,并标出它与劣弧的交点E(保留作图痕迹,不写作法);(2)、若(1)中的点E到弦BC的距离为3,求BC的长.22. 已知关于 的一元二次方程 .(1)、求证:无论 为任何实数,此方程总有两个实数根;(2)、若方程的两个实数根为 、 ,满足 ,求 的值;(3)、若 △ 的斜边为5,另外两条边的长恰好是方程的两个根 、 ,求 的内切圆半径.23. 2022年2月4日,第24届冬季奥林匹克运动会将在北京举行,吉祥物“冰墩墩”备受人民的喜爱. 某商店经销一种吉祥物玩具,销售成本为每件40元,据市场分析,若按每件80元销售,一个月能售出100件;销售单价每降1元,月销售量就增加5件,针对这种玩具的销售情况,请解答以下问题:(1)、设每件玩具的售价为x元(x为正整数),每月的销售量为y件.直接写出y与x的函数关系式;(2)、设该商店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该商店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定吉祥物玩具的销售单价?