广东省茂名市茂南区2022年中考第二次模拟考试数学试题

试卷更新日期：2023-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 在下面的四个数中，最小的是（）

A、－2 B、－ $\sqrt{3}$ C、1 D、0

查看试题解析
2. 2022年初，根据当地疫情防控要求，从省外返回的人员原则上需要自行居家观察14天，减少外出活动.14天的时间有1209600秒，1209600用科学记数法表示为（）

A、 $0.12096 \times 1 0^{7}$ B、 $1.2096 \times 1 0^{6}$ C、 $1.2096 \times 1 0^{- 6}$ D、 $12.096 \times 1 0^{5}$

查看试题解析
3. 剪纸是我国古老的民间艺术．下列四个剪纸图案为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，矩形纸片的一条边经过含有30°角的直角三角板的直角顶点，矩形纸片的一组对边与三角板的两条直角边相交形成∠1和∠2，若∠2＝120°，则∠1的度数为（）

A、15° B、30° C、60° D、120°

查看试题解析
5. 下列说法正确的是（）

A、“三角形的外角和是360°”是不可能事件 B、调查某批次汽车的抗撞击能力适合用全面调查 C、了解北京冬奥会的收视率适合用抽样调查 D、从全校1500名学生中抽取100名调查了解寒假阅读情况，抽取的样本容量为1500

查看试题解析
6. 点 $Q (- 1 ， - 2)$ 到x轴的距离为（）

A、 $- 1$ B、1 C、 $- 2$ D、2

查看试题解析
7. 关于 m、n 的整式 m² + kmn + 9n ²是完全平方式，则 k 的值为（）

A、6 B、- 6 C、± 6 D、± 18

查看试题解析
8. 某同学借了一本书，共140页，要在一周内读完．当他读了这本书的半时，发现平均每天要多读21页才能刚好在借期内读完，他读这本书的前一半时，平均每天读多少页？设他读这本书的前一半时，平均每天读 $x$ 页，则下列方程中正确的是 $($ $)$

A、 $\frac{70}{x} + \frac{70}{x - 21} = 7$ B、 $\frac{70}{x} + \frac{70}{x + 21} = 7$ C、 $\frac{140}{x} + \frac{140}{x - 21} = 7$ D、 $\frac{140}{x} + \frac{140}{x + 21} = 7$

查看试题解析
9. 如图，两个反比例函数 $y = \frac{k_{1}}{x}$ 和 $y = \frac{k_{2}}{x}$ 在第一象限内的图象分别是 $l_{1}$ 和 $l_{2}$ ，设点P在 $l_{1}$ 上， $P C ⊥ x$ 轴于点C，交 $l_{2}$ 于点 $A ， P D ⊥ y$ 轴于点D，交 $l_{2}$ 于点B，则四边形 $P A O B$ 的面积为（）．

A、 $k_{1} + k_{2}$ B、 $k_{1} - k_{2}$ C、 $k_{1} k_{2}$ D、 $k_{2} - k_{1}$

查看试题解析
10. 如图，在边长为2的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的是（）
①△CMP∽△BPA；②△CNP的周长始终不变；③当P为BC中点时，AE为线段NP的中垂线；④线段AM的最小值为 $\sqrt{5}$ ；⑤当△ABP≌△ADN时，BP＝2 $\sqrt{2}$ －2

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 5的平方根是．

查看试题解析
12. 因式分解： $x y^{2} - x =$ ．

查看试题解析
13. 一元一次不等式组 ${\begin{array}{l} x - 1 \leq 0 \\ 2 - \frac{1}{3} x > 0 \end{array}$ 的解集为．

查看试题解析
14. 若线段AB＝2，点C是线段AB的黄金分割点，且AC＜BC，则线段BC的长为．（保留根号）

查看试题解析
15. 若 $2 a - b + 1 = 0$ ，则 $4 a - 2 b + 2022 =$ ．

查看试题解析
16. 小华家客厅有一张直径为 $1.2 m ，$ 高为 $0.8 m$ 的圆桌 $A B ，$ 有一盏灯 $E$ 到地面垂直距离 $E F$ 为 $2 m ，$ 圆桌的影子为 $C D ， F C = 2$ ，则点 $D$ 到点 $F$ 的距离为．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A C B = 45 ° ， A B = 4 ， ∠ B A C = 60 °$ ， D是边 $B C$ 上的一个动点，连接 $A D$ ，并将线段 $A D$ 绕点A逆时针旋转 $60 °$ 后得线段 $A D^{'}$ ，连接 $B D^{'}$ ，在点D运动过程中，线段 $B D^{'}$ 长度的最小值是．

查看试题解析

三、解答题

18. 计算： ${(- 2)}^{3} + \sqrt{16} - 2 s i n 3 0^{0} + {(2022 - π)}^{0}$

查看试题解析
19. 先化简 $\frac{4}{a + 3} - \frac{6}{a^{2} - 9} \div \frac{2}{a - 3}$ ，再求代数式的值，其中 $a = \sqrt{3} - 3$ ．

查看试题解析
20. 如图，平行四边形 $A B C D$ 中， $A B < B C$ .

(1)、利用尺规作图，在 $B C$ 边上确定点 $E$ ，使点 $E$ 到边 $A B$ ， $A D$ 的距离相等（不写作法，保留作图痕迹）；

(2)、若 $A D = 8$ ， $D C = 5$ ，求 $C E$ 的长.

查看试题解析
21. 某中学积极响应上级课后延时服务要求，进一步丰富学生课余生活，拟调整兴趣活动小组，为此进行了一次抽样调查，根据采集到的数据绘制的统计图（不完整）如下：
请你根据图中提供的信息，完成下列问题：

(1)、图1中，“编程”部分所对应的圆心角为度；

(2)、此次调查共抽查了名学生；

(3)、在图2中，将“篮球”部分的图形补充完整；

(4)、若该中学现有学生3200人，请估计现有学生中爱好“书法”的人数．

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，D、E分别是边AC、AB的中点，连接CE、DE，过D点作DF∥CE交BC的延长线于F点．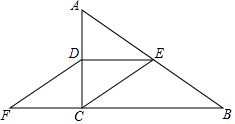

(1)、证明：四边形DECF是平行四边形；

(2)、若AB＝13cm，AC＝5cm，求四边形DECF的周长．

查看试题解析
23. 如图，某养猪户想用29米长的围栏设计一个矩形的养猪圈，其中猪圈一边靠墙MN，另外三边用围栏围住，在BC边开个门（宽度为1米），MN的长度为15m，

(1)、为了让围成的猪圈（矩形ABCD）面积达到112m² ，请你帮忙计算一下猪圈的长与宽分别是多少？

(2)、当猪圈的长与宽分别是多少时，猪圈的面积达到最大？

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A C = 12$ ， $A B = 6$ ，点 $D$ 在 $B C$ 上，连接 $A D$ ，过点 $D$ 作 $A D$ 的垂线交 $A C$ 于点 $E$ ，连接 $D E$ ， $△ A D E$ 的外接圆交直线 $A B$ 于点 $F .$ 圆心为 $O$ ．

(1)、若 $A D$ 平分 $∠ B A C$ ；
①判断 $B C$ 与 $⊙ O$ 的位置关系，并说明理由；
②求出此时图中阴影部分的面积；

(2)、若 $C D = 5 \sqrt{3}$ ，求 $⊙ O$ 的直径．

查看试题解析
25. 如图，已知二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $C (2 ， - 3)$ ，且与x轴交于原点及点 $B (8 ， 0)$ ，点A为抛物线的顶点.

(1)、求二次函数的表达式；

(2)、在抛物线的对称轴上是否存在点M，使 $△ A B M$ 是等腰三角形？如果存在，请求出点M的坐标.如果不存在，请说明理由；

(3)、若点P为⊙O上的动点，且⊙O的半径为 $2 \sqrt{2}$ ，求 $\frac{1}{2} A P + P B$ 的最小值.

查看试题解析