广东省揭阳市2022年中考数学第一次模拟试卷

试卷更新日期：2023-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数- $\sqrt{3}$ ， -2， $\frac{1}{2}$ ， $\sqrt{2}$ 中，最小的是（）

A、- $\sqrt{3}$ B、-2 C、 $\frac{1}{2}$ D、 $\sqrt{2}$

查看试题解析
2. 如图所示的几何体是一个正三棱柱，以下不是其三视图的是（）

A、 B、 C、 D、

查看试题解析
3. 2019年4月10日，人类首张黑洞图片问世，该黑洞位于室女座一个巨椭圆星系 $M 87$ 的中心，距离地球 $5500$ 万光年.将数据 $5500$ 万用科学记数法表示为（）

A、 $5500 \times 10^{4}$ B、 $55 \times 10^{6}$ C、 $5.5 \times 10^{7}$ D、 $5.5 \times 10^{8}$

查看试题解析
4. 某班七个兴趣小组人数分别为4，4，5，5，x，6，7，已知这组数据的平均数是5，则这组数据的中位数和众数分别是（）

A、5，5 B、5，4 C、4，4 D、4，5

查看试题解析
5. 关于x的方程 $(a - 2) x^{2} + \sqrt{a - 1} x + 1 = 0$ 是一元二次方程，则 $a$ 的取值范围是（）

A、 $a \neq 2$ B、 $a \geq 1$ C、 $a > 1$ 且 $a \neq 2$ D、 $a \geq 1$ 且 $a \neq 2$

查看试题解析
6. 在△ABC中，∠A= $\frac{1}{2}$ ∠B= $\frac{1}{3}$ ∠C，则△ABC是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
7. 一个正多边形的外角与相邻的内角的度数之比为1：3，则这个多边形的边数是（）

A、8 B、9 C、6 D、5

查看试题解析
8. 下列方程中，两根之和是3的是（）

A、x²﹣3x+ $\frac{5}{2}$ =0 B、﹣x²+3x+ $\frac{5}{2}$ =0 C、x²+3x﹣ $\frac{5}{2}$ =0 D、x²+3x+ $\frac{5}{2}$ =0

查看试题解析
9. 抛物线y＝﹣x²向上平移2个单位，再向左平移3个单位得到的抛物线解析式为（）

A、y＝﹣（x+3）²+2 B、y＝﹣（x﹣3）²+2 C、y＝﹣（x+3）²﹣2 D、y＝﹣（x﹣3）²﹣2

查看试题解析
10. 观察下列一组数：- $\frac{1}{3}$ ， $\frac{4}{5}$ ， - $\frac{9}{7}$ ， $\frac{16}{9}$ ， - $\frac{25}{11}$ ， ……，它们是按照一定规律排列的，那么这组数的第n个数是（）

A、 $\frac{n^{2}}{2 n + 1}$ B、（-1）n $\frac{n^{2}}{2 n + 1}$ C、（-1）n $\frac{n^{2}}{2 n - 1}$ D、（-1）n^-1 $\frac{n^{2}}{2 n + 1}$

查看试题解析

二、填空题

11. 计算： ${(- \frac{1}{2})}^{2019} \times 2^{2020} =$ .

查看试题解析
12. 已知x＝-1是方程x²+ax+4＝0的一个根，则方程的另一个根为．

查看试题解析
13. 一个角的度数为 $30 ° 2 1^{'}$ ，则这个角的余角的度数是．

查看试题解析
14. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $c o s A = \frac{3}{5}$ ， $A B = 15$ ，则AC的长是．

查看试题解析
15. 已知代数式 $m^{2} + 2 m - 5$ 的值等于 $7$ ，则代数式 $2 m^{2} + 4 m + 1 =$ ．

查看试题解析
16. 如图，已知四边形ABCD和四边形BEFM均为正方形，以B为圆心，以BE为半径作弧EM．若大正方形的边长为8厘米，则图中阴影部分的面积为．（结果保留 $π$ ）

查看试题解析
17. 如图，直角ABC的周长为2008，在其内部有五个小直角三角形，则这五个小直角三角形的周长为．

查看试题解析

三、解答题

18.

(1)、计算： $| - 1 | + {(- \frac{1}{3})}^{- 1} + 201 9^{0} - 4 c o s 60 °$ ；

(2)、先化简，再求值： $\frac{x - 2}{x - 1} \div (1 - \frac{1}{x^{2} - 2 x + 1})$ ，其中 $x = \sqrt{2}$ ．

查看试题解析
19. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $A D = 8$ ，将矩形折叠，折痕为 $E F$ ，使点C与点A重合，点D与点G重合，连接 $C F$ ．

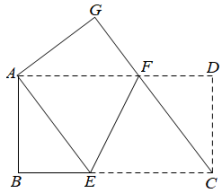(1)、判断四边形 $A E C F$ 的形状，并说明理由；

(2)、求折痕 $E F$ 的长．

查看试题解析
20. 甲、乙两人每次都从五个数 $- 2 ， - 1$ ， 0，1，2中任取一个，分别记作x、y．在平面直角坐标系中有一圆心在原点，半径为2的圆．

(1)、能得到多少个不同的数组 $(x ， y)$ ？

(2)、若把（1）中得到的数组作为点 $P$ 的坐标 $(x ， y)$ ，则点 $P$ 落在圆内的概率是多少？

查看试题解析
21. 疫情期间为搞活经济，某街道拟建A，B两类摊位，每个A类摊位的占地面积比每个B类摊位的占地面积少3平方米.建A类摊位每平方米的费用为40元，建B类摊位每平方米的费用为50元.用120平方米建A类摊位的个数恰好比用同样面积建B类摊位个数多2个.

(1)、求每个A，B类摊位占地面积各为多少平方米？

(2)、该街道拟建A，B两类摊位共60个，且A类摊位的数量不少于B类摊位数量的2倍.求建造这60个摊位的最大费用.

查看试题解析
22. 如图， $△ A B F$ 中， $E$ 是边 $A F$ 的中点，点 $C$ 在 $B F$ 上，作 $A D / / B F$ 交 $C E$ 的延长线于点 $D$ ．

(1)、求证： $△ A D E$ ≌ $△ F C E$ ．

(2)、若 $∠ C E F = 90 °$ ， $A D = 5$ ， $C E = 4$ ，求点 $E$ 到 $B F$ 的距离．

查看试题解析
23. 如图1，已知 $A B$ 是 $⊙ O$ 的直径，D是线段 $A B$ 延长线上的一个动点，直线 $D F ⊥$ 射线 $A B$ 于点D，当直线 $D F$ 绕点D逆时针旋转 $α (0 ° < α < 180 °)$ 时，与 $⊙ O$ 交于点C，且运动过程中，保持 $C D = O A$ ．

(1)、当直线 $D F$ 与 $⊙ O$ 相切于点C时，求旋转角的度数；

(2)、当直线 $D F$ 与半圆O相交于点C时（如图2所示），设另一交点为E，连接 $A E$ ， $O C$ ，若AE//OC，试判断 $A E$ 与 $O D$ 之间的数量关系，并说明理由．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = a x + b$ 与双曲线 $y = \frac{k}{x}$ （ $x > 0$ ）交于 $A (1 ， 3)$ ， $B (3 ， m)$ 两点，与x轴交于点C，与y轴交于点D，连接 $O A$ ， $O B$ .

(1)、求a，b，k的值；

(2)、求 $△ O A B$ 的面积；

(3)、在x轴上是否存在点P，使 $△ P C D$ 的面积等于 $△ O A B$ 的面积的3倍.若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由.

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + c$ 的顶点G的坐标为 $(- 1 ， - 4)$ ，与x轴交于A，B两点，且 $A B = 4$ ．

(1)、求此抛物线的解析式．

(2)、已知点 $(x_{1} ， y_{1})$ ， $(x_{1} + 1 ， y_{2})$ 均在此抛物线上，且 $y_{2} < y_{1}$ ，请直接写出 $x_{1}$ 的取值范围．

(3)、将该抛物线沿x轴平移，当抛物线与坐标轴有且只有两个交点时停止移动，得到新抛物线L，点M是线段AB（A，B为原抛物线与x轴的交点）上的一点，过点M作 $M N ⊥ x$ 轴交新抛物线L于点N，求点N的纵坐标 $y_{N}$ 的取值范围．

查看试题解析