广东省揭阳市2022年中考数学第三次模拟测试卷

试卷更新日期：2023-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个数中，最小的是（）

A、|﹣1.5| B、0 C、﹣（﹣3） D、﹣3

查看试题解析
2. 下列用七巧板拼成的图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各式中，不属于二次根式的是（）

A、 $\sqrt{- x}$ （x≤0） B、 $\sqrt{1 + b^{2}}$ C、 $\sqrt{（ a - b ）^{2}}$ D、 $\sqrt{- 1 - x^{2}}$

查看试题解析
4. 已知 $a$ 、 $b$ 两数在数轴上的位置如图所示，则化简代数式 $| a + b | + | b + 1 |$ 的结果是（）

A、 $a - 1$ B、 $2 a$ C、 $2$ D、 $2 a - 2$

查看试题解析
5. 如图，某同学在制作正方体模型的时候，在方格纸上画出几个小正方形（图中阴影部分），但是由于疏忽少画了一个，请你给他补上一个，使之可以组合成正方体，你一共有（）种画法．

A、2 B、3 C、4 D、5

查看试题解析
6. 下列运算中，正确的是（）

A、x⁸÷x²＝x⁴ B、2x-x＝1 C、（x³）³＝x⁶ D、x+x＝2x

查看试题解析
7. 如果点C是线段AB的黄金分割点（AC>BC），则下列比例式正确的是（）

A、AB∶AC=AC∶BC B、AB∶BC=BC∶AC C、AC∶BC=BC∶AB D、AC∶AB=AB∶BC

查看试题解析
8. 如图是小明用七巧板拼成的一个机器人，其中全等三角形有（）

A、1 对 B、2 对 C、3 对 D、4 对

查看试题解析
9. 如图，函数 $y = \frac{1}{x}$ (x>0)和 $y = \frac{3}{x}$ (x>0)的图象分别是 $l_{1}$ 和 $l_{2}$ .设点P在 $l_{2}$ 上，PA∥y轴交 $l_{1}$ 于点A，PB∥x轴，交 $l_{1}$ 于点B，△PAB的面积为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{3}{4}$

查看试题解析
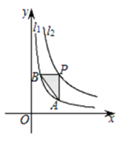10. 如图1是一张圆形纸片，小可同学进行了如下连续操作：
⑴将圆形纸片左右对折，上下对折，得到折痕AB与CD互相垂直，垂足为点M，如图2．
⑵将圆形纸片沿EF折叠，使B、M两点重合，折痕EF与AB相交于N，连接AE、AF，BE、BF，如图3．
小可得到了以下结论：①CD//EF；② $∠ E A F = \frac{1}{2} ∠ E B F$ ；③ $△ A E F$ 为等边三角形；④ $E N \times F N = A M^{2} - B N^{2}$ ．以上结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一个不透明的袋中有四张形状大小质地完全相同的卡片，它们上面分别标有数字 $1 ， 2 ， 3 ， 4$ ，随机抽取一张卡片不放回，再随机抽取一张卡片，则两次抽取的卡片上数字之和为奇数的概率是.

查看试题解析
12. 如图，在△ABC中，∠B=30°，∠C=50°，通过观察尺规作图的痕迹，∠DAE的度数是．

查看试题解析
13. 解方程 $(\frac{x}{x + 2})^{2} + 3 (\frac{x}{x + 2}) + 2 = 0$ ，如果设=y，那么得到关于y的整式方程是．

查看试题解析
14. 如图，a，b，c在数轴上的位置如图所示，化简 $\sqrt{b^{2}} - | b + c | - \sqrt{(c - a)^{2}}$ 的结果为

查看试题解析
15. 已知二次函数y=（x+1）（x-a）的对称轴为直线x=2，则a的值是．

查看试题解析
16. 如图，在综合与实践活动课上，同学们用圆心角为 $120 °$ ，半径为 $6 cm$ 的扇形纸片卷成了一个无底圆锥形小帽，则这个小纸帽的底面半径 $r$ 等于 $cm$ .

查看试题解析
17. 在四边形 $A C B D$ 中， $A C ⊥ B C$ 且 $B C = 2$ ， $A D = 3$ ， $A B = 4$ ， $B D = 5$ ，则 $∠ C A D =$ .

查看试题解析

三、解答题

18. 先化简，再求值： $\frac{x - 4}{x^{2} - 1} \div \frac{x^{2} - 3 x - 4}{x^{2} + 2 x + 1} \div \frac{1}{x - 1}$ ，其中 $x = {(\frac{1}{3})}^{- 2}$

查看试题解析
19. 家住两相邻小区的丽丽和娟娟在一次数学课后，进行了一次数学实践活动．如图，在同一水平面从左往右依次是一座小山 $F N$ 、丽丽家所在的小洋房 $C D$ 、娟娟家所在的居民楼 $A B$ ，实践内容为测量小山的高度 $F N .$ 家住顶楼的娟娟在窗户 $A$ 处测得丽丽家小洋房底部 $D$ 点的俯角为 $∠ 1$ ，丽丽在自家窗户 $C$ 处测得小山山顶的一棵竖直的大树顶端 $E$ 的仰角为 $∠ 2$ ，且 $∠ 1$ 与 $∠ 2$ 互余，已知两家水平距离 $B D = 100$ 米，且 $A B = D N$ ，大树高度 $E F = 8$ 米，丽丽家小洋房 $C D = 10$ 米，点 $E$ 、 $F$ 、 $N$ 在一条直线上， $A B ⊥ B N$ ， $C D ⊥ B N$ ， $E N ⊥ B N$ ，请根据以上信息求小山的高度 $F N$ ．

查看试题解析
20. 现有3个不等式；① $2 x + 3 < - 1$ ， ② $- 5 x > 15$ ， ③ $3 (x - 1) > 6$ ．

(1)、从中任选两个不等式组成一个不等式组，并在下面横线上列出你所选的不等式组：．

(2)、求出（1）中你所列不等式组的解集．

查看试题解析
21. 如图，等边 $△ A B C$ 的边长是2， $D$ ， $E$ 分别为 $A B$ ， $A C$ 的中点，延长 $B C$ 至点 $F$ ，使 $C F = \frac{1}{2} B C$ ，连接 $C D$ 和 $F E$ ．

(1)、求证：四边形 $C D E F$ 为平行四边形；

(2)、求 $E F$ 的长．

查看试题解析
22. 太仓人杰地灵，为了了解学生对家乡历史文化名人的知晓情况，某校对部分学生进行了随机抽样调查，并将调查结果绘制成如图所示统计图的一部分.

根据统计图中的信息，回答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、在扇形统计图中，“了解很少”所在扇形的圆心角是度；

(3)、若全校共有学生1300人，那么该校约有多少名学生“基本了解”太仓的历史文化名人？

查看试题解析
23. 今年3月，德宏瑞丽受疫情影响，采取了“封城措施”．封城期间，某公司安排大、小货车共20辆，分别从A、B两地运送320吨物资到德宏瑞丽，支援瑞丽抗击疫情，每辆大货车装25吨物资，每辆小货车装10吨物资，这20辆货车恰好装完这批物资，已知这两种货车的运费如下表：

目的地

车型

A地（元/辆）

B地（元/辆）

大货车

900

1000

小货车

500

700

要安排上述装好物资的20辆货车中的10辆从A地出发，其余从B地出发．

(1)、这20辆货车中，大货车、小货车各有多少辆？

(2)、设从A地出发的大货车有 $x$ 辆（大货车不少于5辆），这20辆货车的总运费为 $y$ 元，求总运费 $y$ 的最小值．

查看试题解析
24. 如图1，在矩形 $A B C D$ 中， $A B = 8$ ， $A D = 10$ ， E是 $C D$ 边上一点，连接 $A E$ ，将矩形 $A B C D$ 沿 $A E$ 折叠，顶点D恰好落在 $B C$ 边上点F处，延长 $A E$ 交 $B C$ 的延长线于点G．

(1)、求线段 $C E$ 的长；

(2)、如图2，M，N分别是线段 $A G ， D G$ 上的动点（与端点不重合），且 $∠ D M N = ∠ D A M$ ，设 $D N = x$ ．
①求证四边形AFGD为菱形；
②是否存在这样的点N，使 $△ D M N$ 是直角三角形？若存在，请求出x的值；若不存在，请说明理由．

查看试题解析
25. 已知抛物线 $y = - x^{2} + b x + c$ （b，c为常数）经过点 $A (0 ， 3)$ ， $B (- 1 ， 0)$ .

(1)、求抛物线的解析式及对称轴；

(2)、在平面直角坐标系xOy中，当m，n满足 $m + n = m n$ 时，就称点 $M (m ， \frac{m}{n})$ 为“美好点”.若点P、Q（P在Q左边）为抛物线上的“美好点”，点N为抛物线上P、Q之间的一点（包含P、Q），求点N的横坐标 $x_{N}$ 及纵坐标 $y_{N}$ 的取值范围.

查看试题解析