安徽省合肥市2022年中考六区联考试卷（二）数学试题

试卷更新日期：2023-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个数中，最大的数是（）

A、1 B、0 C、－1 D、－2

查看试题解析
2. 计算 ${(- a^{2})}^{3}$ 的结果是（）

A、 $a^{5}$ B、 $- a^{5}$ C、 $a^{6}$ D、 $- a^{6}$

查看试题解析
3. 如图所示，水平放置的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 2021年，我国国内生产总值达到114万亿元．数据114万亿用科学记数法表示为（）

A、 $114 \times 1 0^{12}$ B、 $1.14 \times 1 0^{6}$ C、 $1.14 \times 1 0^{14}$ D、 $1.14 \times 1 0^{10}$

查看试题解析
5. 若关于x的一元二次方程 $x (x - 2) = 2 m x$ 有两个相等的实数根，则实数m的值为（）

A、－1 B、0 C、－1或0 D、4或1

查看试题解析
6. 某校为了了解学生家长对“双减”政策的认知情况，随机抽查了部分学生家长进行调查，将抽查的数据结果进行统计，并绘制两幅不完整统计图（A：不太了解．B：基本了解，C：比较了解，D：非常了解），根据图中信息可知，下列结论错误的是（）

A、本次调查的样本容量是50 B、“非常了解”的人数为10人 C、“基本了解”的人数为15人 D、“比较了解”部分所对应的圆心角度数为120°

查看试题解析
7. 一种商品，先提价20%，再降价10%，这时的价格是2160元．则该商品原来的价格是（）

A、2400元 B、2200元 C、2000元 D、1800元

查看试题解析
8. 如图，在 $△ A B C$ 中，AB＝AC，∠A＝20°，点D为AC边上的一点，∠DBC＝50°，点E为AB上一点，∠ECB＝20°，则∠BDE的度数为（）

A、10° B、15° C、20° D、25°

查看试题解析
9. 设a、b、c为实数，且满足a－b＋c＜0，a＋b＋c＞0，则下列结论正确的是（）

A、 $b^{2} > 4 a c$ B、 $b^{2} \leq 4 a c$ 且 $a \neq 0$ C、 $b^{2} > 4 a c$ 且 $a > 0$ D、 $b^{2} > 4 a c$ 且 $a < 0$

查看试题解析
10. 在四边形ABCD中．∠B＝∠C＝90°，AB＋DC＝AD，BC＝6，则AB·DC的值为（）

A、 $6 \sqrt{3}$ B、 $6 \sqrt{2}$ C、9 D、12

查看试题解析

二、填空题

11. 计算： $\sqrt{2} \times \sqrt{8}$ = .

查看试题解析
12. 用一个 $a$ 的值说明命题“如果 $a^{2} \geq 1$ ，那么 $a \geq 1$ ”是错误的，这个值可以是a＝．

查看试题解析
13. 如图，在 $⊙ O$ 中，AB与 $⊙ O$ 相切于点A，连接OB交 $⊙ O$ 于点C，过点A作 $A D ∥ O B$ 交 $⊙ O$ 于点D，连接CD．若∠B＝40°，则∠OCD的度数为．

查看试题解析
14. 如图，在平面直角坐标系中，正方形OABC的顶点A在x轴正半轴上，顶点C在y轴正半轴上，抛物线 $y = a x^{2} - 2 a x + c$ 经过点B、C．

(1)、点B的坐标为．

(2)、若抛物线 $y = a x^{2} - 2 a x + c$ 的顶点在正方形OABC的内部，则a的取值范围是．

查看试题解析

三、解答题

15. 先化简，再求值： $(\frac{x^{2} - 1}{x^{2} - 2 x + 1} - \frac{1}{1 - x}) \div \frac{x + 2}{x^{3} - x^{2}}$ ，其中 $x = - 2$ ．

查看试题解析
16. 为了美化校园，校团委植树节在清华路两旁植树，甲团小组计划用若干天完成校团委的植树工作，从第三个工作日起，乙团小组加入此项工作，且甲、乙两团小组工作效率相同，结果提前3天完成任务，求甲团小组计划完成此项工作的天数．

查看试题解析
17. $△ A B C$ 在方格中的位置如图所示．
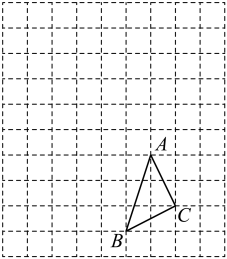
（ 1 ）请在方格纸上建立平面直角坐标系，使得A、B两点的坐标分别为A（2，－1）、B（1，－4）．并求出C点的坐标；
（ 2 ）作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，再作出 $△ A B C$ 以坐标原点为旋转中心，旋转180°后的 $△ A_{2} B_{2} C_{2}$ ．
（ 3 ）观察 $△ A_{1} B_{1} C_{1}$ 和 $△ A_{2} B_{2} C_{2}$ ，其中一个三角形能否由另一个三角形经过某种变换而得到的？若能请指出是什么变换？

查看试题解析
18. 为美化市容，某广场要在人行雨道上用10×20的灰、白两色的广场砖铺设图案，设计人员画出的一些备选图案如图所示．
[观察思考]图1灰砖有1块，白砖有8块；图2灰砖有4块，白砖有12块；以此类推．

(1)、[规律总结]图4灰砖有块，白砖有块；图n灰砖有块时，白砖有块；

(2)、[问题解决]是否存在白砖数恰好比灰砖数少1的情形，请通过计算说明你的理由．

查看试题解析
19. 幸福家园小区车库入口处安装了“曲臂杆”如图1，OA⊥AB，OA＝1米，点O是臂杆转动的支点，点C是曲臂杆两段的连接点，曲臂杆CD部分始终与AB平行．如图2，曲臂杆初始位置时O、C、D三点共线，当曲臂杆升高到OE时，∠AOE＝120°，点E到AB的距离是1.7米，当曲臂杆升高到OF时，∠COF＝66°，则点F到AB的距离是多少米？（结果精确到0.1来，参考数据： $\sqrt{3} \approx 1.73$ ， $s i n 66 ° \approx 0.9$ ）

查看试题解析
20. 如图，四边形ABCD内接于 $⊙ O$ ， AB为直径， $\overset{⌢}{D C}$ 所对圆心角为90°，连接AC，BD交于点E．

(1)、求证：BC＝CE；

(2)、当 $D C = \sqrt{2}$ 时，求 $⊙ O$ 的半径．

查看试题解析
21. 质检员小李对车间3月21日生产的15个零件进行了测量，所得数据整理如下表：
编号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
⑪
⑫
⑬
⑭
⑮
尺寸/mm
50.8
48.6
50.6
50.1
49.4
50.3
49.7
49.9
49.2
49.6
50.4
49.1
50.7
47.8
a
尺寸/mm
产品等次
$49.7 \leq x \leq 50.3$
特等品
$49.5 \leq x \leq 50.5$
优等品
$49.0 \leq x \leq 51.0$
合格品
x＜49.0或x＞51.0
残次品
（注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品（含特等品）计算在内．）

(1)、已知这次抽检的合格率为80%，请判断编号为⑮的产品是否为合格品，并说明理由．

(2)、求出此次抽检出的优等品尺寸的中位数．

(3)、将这些优等品分成两组，一组尺寸大于50.0mm，另一组尺寸不大于50.0mm，从这两组中各随机抽取1件进行复检，请求出抽取到的2件产品都是特等品的概率．

查看试题解析
22. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} + b x + c$ 与直线 $y = \frac{1}{2} x + b$ 交于A、B两点，其中点A在x轴上，已知A点坐标（1，0），点P是直线AB上方的抛物线上一动点（不与点A、B重合），连接PA，直线AB，PA分别交y轴于点D，E，过P作y轴的平行线交直线于点C．

(1)、求二次函数的解析式及B点的坐标；

(2)、求当PC长最大时，线段DE的长．

查看试题解析
23. 在四边形ABCD中，对角线AC，BD交于点O，AC平分∠BAD，∠BAC＝∠CBD，AC＝AD．

(1)、求证：
① $△ A B C ≌ △ A O D$ ；
② $D O^{2} = O C \cdot A C$ ；

(2)、当∠BAD＝90°时，求 $\frac{A B}{A D}$ 的值．

查看试题解析

编号	①	②	③	④	⑤	⑥	⑦	⑧	⑨	⑩	⑪	⑫	⑬	⑭	⑮
尺寸/mm	50.8	48.6	50.6	50.1	49.4	50.3	49.7	49.9	49.2	49.6	50.4	49.1	50.7	47.8	a

尺寸/mm	产品等次
$49.7 \leq x \leq 50.3$	特等品
$49.5 \leq x \leq 50.5$	优等品
$49.0 \leq x \leq 51.0$	合格品
x＜49.0或x＞51.0	残次品