安徽省滁州市定远县2022年中考数学一模试卷
试卷更新日期:2023-03-07 类型:中考模拟
一、单选题
-
1. ﹣ 的相反数是( )A、﹣ B、﹣ C、 D、2. 2022年3月5日,十三届全国人大五次会议在京召开,国务院总理李克强做政府工作报告,今年主要预期目标粮食产量保持在1.3万亿斤以上,其中1.3万亿用科学记数法表示为( )A、1.3×10 B、1.3×10 C、1.3×10 D、13×103. 如图,该几何体的左视图是( )
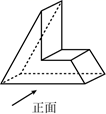 A、
A、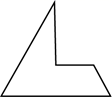 B、
B、 C、
C、 D、
D、 4. 分解因式2x2﹣8结果正确的是( )A、2(x+2)(x﹣2) B、2(x﹣2)2 C、2(x2﹣8) D、2(x+2)25. 将一副直角三角板按如图方式摆放,若直线a∥b,则∠1的大小为( )
4. 分解因式2x2﹣8结果正确的是( )A、2(x+2)(x﹣2) B、2(x﹣2)2 C、2(x2﹣8) D、2(x+2)25. 将一副直角三角板按如图方式摆放,若直线a∥b,则∠1的大小为( ) A、75° B、60° C、45° D、30°6. 如图,已知直线 与坐标轴分别交于A、B两点,那么过原点O且将 的面积平分的直线 的解析式为( )
A、75° B、60° C、45° D、30°6. 如图,已知直线 与坐标轴分别交于A、B两点,那么过原点O且将 的面积平分的直线 的解析式为( ) A、 B、 C、 D、7. 连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘.将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )
A、 B、 C、 D、7. 连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘.将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为( )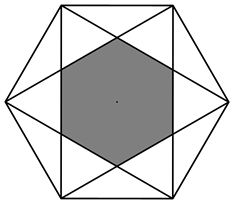 A、 B、 C、 D、8. 如图,在菱形ABCD中, , 点E,F分别在边AB,BC上, , 的周长为 , 则AD的长为( )
A、 B、 C、 D、8. 如图,在菱形ABCD中, , 点E,F分别在边AB,BC上, , 的周长为 , 则AD的长为( ) A、 B、 C、 D、9. 已知a、b、c满足a+c=b,且 , 则下列结论不正确的是( )A、若b>c>0,则a>0 B、若c=1,则a(a-1)=1 C、若a-c=2,则ac=2 D、若bc=1,则a=110. 如图,在△ABC和△AED中,∠CAB=∠DAE=36°,AB=AC、AE=AD,连接CD,连接BE并延长交AC,AD于点F、G.若BE恰好平分∠ABC,则下列结论:①DE=GE;②CD∥AB;③∠ADC=∠AEB;④BF=CF•AC.其中正确的个数为( )
A、 B、 C、 D、9. 已知a、b、c满足a+c=b,且 , 则下列结论不正确的是( )A、若b>c>0,则a>0 B、若c=1,则a(a-1)=1 C、若a-c=2,则ac=2 D、若bc=1,则a=110. 如图,在△ABC和△AED中,∠CAB=∠DAE=36°,AB=AC、AE=AD,连接CD,连接BE并延长交AC,AD于点F、G.若BE恰好平分∠ABC,则下列结论:①DE=GE;②CD∥AB;③∠ADC=∠AEB;④BF=CF•AC.其中正确的个数为( )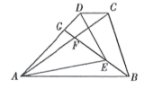 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. (-a2)3= .12. 已知关于x的方程有两个不相等的实数根,则k的取值范围是 .13. 如图,BC是⊙O的直径,A是⊙O外一点,连接AC交⊙O于点E,连接AB并延长交⊙O于点D,若∠A=30°,则∠DOE的大小是度.
 14. 在平面直角坐标系中,已知抛物线y=mx-2mx+m-2(m>0).(1)、抛物线的顶点坐标为;(2)、点M(x1 , y1)、N(x2 , y2)(x1<x2≤3)是拋物线上的两点,若y1<y2 , x2-x1=2,则y2的取值范围为(用含 m的式子表示)
14. 在平面直角坐标系中,已知抛物线y=mx-2mx+m-2(m>0).(1)、抛物线的顶点坐标为;(2)、点M(x1 , y1)、N(x2 , y2)(x1<x2≤3)是拋物线上的两点,若y1<y2 , x2-x1=2,则y2的取值范围为(用含 m的式子表示)三、解答题
-
15. 先化简再求值: ,其中 .16. 如图,在平面直角坐标系中,线段的端点都在网格线的交点上(每个小方格都是边长为1个单位长度的正方形),按要求完成下列任务.
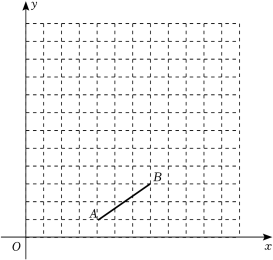
( 1 )以点为旋转中心,将线段逆时针旋转 , 得到线段 , 画出线段;
( 2 )以原点为位似中心,将线段在第一象限扩大3倍,得到线段 , 画出线段(点 , 的对应点分别是 , ).
17. 在平面直角坐标系中,设函数:(是常数, , )与函数,(是常数,)的图象交于点A,点A关于y轴的对称点为点B.若点B的坐标为 . (1)、求 , 的值;(2)、当时,直接写出x的取值范围.18. 观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法…,据此解答下面的问题.
(1)、求 , 的值;(2)、当时,直接写出x的取值范围.18. 观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法…,据此解答下面的问题. (1)、填写下表:
(1)、填写下表:图形
挖去三角形的个数
图形1
1
图形2
1+3
图形3
1+3+9
图形4
(2)、根据这个规律,求图n中挖去三角形的个数(用含n的代数式表示);(3)、若图中挖去三角形的个数为 , 求 .19. 如图,小明从B处测得广告牌顶端A的仰角为45°,从C处测得广告牌底部D的仰角为30°,BC、AE均垂直于地面CE,已知CE=10m、BC=2m,水广告牌的高度AD.(结果保留两位小数,参考数据:≈1.414,≈1.732)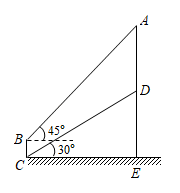 20. 如图,AB是⊙O的直径,点C在⊙O上且不与点A、B重合,∠ABC的平分线交⊙O于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG.
20. 如图,AB是⊙O的直径,点C在⊙O上且不与点A、B重合,∠ABC的平分线交⊙O于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG. (1)、求证:FG=DE;(2)、若AB=4 , FG=4,求AG的长21. 国家规定“中小学生每天在校体育活动时间不低于 ”.为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
(1)、求证:FG=DE;(2)、若AB=4 , FG=4,求AG的长21. 国家规定“中小学生每天在校体育活动时间不低于 ”.为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:组: 组:
组: 组:

请根据上述信息解答下列问题:
(1)、本次调查的人数是人;(2)、请根据题中的信息补全频数分布直方图;(3)、 组对应扇形的圆心角为 ;(4)、本次调查数据的中位数落在组内;(5)、若该市辖区约有80000名初中学生,请估计其中达到国家规定体育活动时间的学生人数约有多少.22. 如图,在平面直角坐标系中,抛物线y=-x+bx+c的图象与坐标轴相交于A、B、C三点,其中点A坐标为(3,0),点B坐标为(-1,0),连接AC、BC,动点P从点A出发,在线段AC上以每秒个单位长度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒. (1)、求b、c的值;(2)、在P、Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?23. 在ΔABC中,∠ACB=90°,AC:BC=m,D是边BC上一点,将ΔABD沿AD折叠得到ΔAED,连接BE.
(1)、求b、c的值;(2)、在P、Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?23. 在ΔABC中,∠ACB=90°,AC:BC=m,D是边BC上一点,将ΔABD沿AD折叠得到ΔAED,连接BE.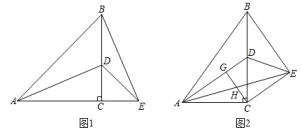 (1)、【特例发现】如图1,当m=1,AE落在直线AC上时.
(1)、【特例发现】如图1,当m=1,AE落在直线AC上时.①求证:∠DAC=∠EBC;
②填空:CD:CE的值为 ▲
(2)、【类比探究】如图2,当m≠1,AE与边BC相交时,在AD上取一点G,使∠ACG=∠BCE,CG交AE于点H,探究CG:CE的值(用含m的式子表示),并写出探究过程;(3)、【拓展运用】在(2)的条件下,当m= , D是BC的中点时,若EB•EH=6,CG的长.