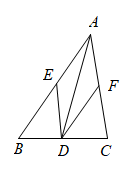陕西省西安市经开区2022-2023学年九年级上学期期末质量检测数学试题卷
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 若 , 则的值为( )A、 B、 C、 D、2. 如图,是一个几何体的三视图,则这个几何体是( )
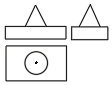 A、
A、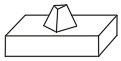 B、
B、 C、
C、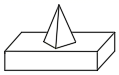 D、
D、 3. 关于x的一元二次方程的一个根是0,则a的值为( )A、1 B、-1 C、1或-1 D、04. 如图,在中, , 点D是的中点,若 , 则的度数是( )
3. 关于x的一元二次方程的一个根是0,则a的值为( )A、1 B、-1 C、1或-1 D、04. 如图,在中, , 点D是的中点,若 , 则的度数是( ) A、 B、 C、 D、5. 若点关于x轴的对称点恰好在反比例函数的图象上,则k的值为( )A、6 B、 C、 D、6. 如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设道路的宽米,则可列方程为( )
A、 B、 C、 D、5. 若点关于x轴的对称点恰好在反比例函数的图象上,则k的值为( )A、6 B、 C、 D、6. 如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使小路的面积为100平方米,设道路的宽米,则可列方程为( ) A、 B、 C、 D、7. 如图,在中, , , 若 , 则等于( )
A、 B、 C、 D、7. 如图,在中, , , 若 , 则等于( ) A、7 B、4 C、8 D、68. 正方形在平面直角坐标系中的位置如图所示,已知点C的坐标是 , 则点A的坐标是( )
A、7 B、4 C、8 D、68. 正方形在平面直角坐标系中的位置如图所示,已知点C的坐标是 , 则点A的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
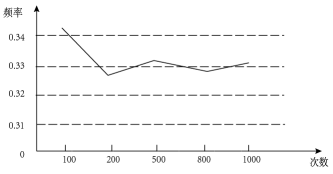
9. 已知不透明的袋中装有红色、黄色、蓝色的乒乓球共120个,某学习小组做“用频率估计概率”的摸球试验(从中随机换出一个球,记下颜色后放回,统计了“摸出球为红色”出现的频率,绘制了如图的折线统计图,那么估计袋中红色球的数目为.(填整十数)
 10. 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是 .
10. 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是 . 11. 如图,已知 , 若 , , , 则的长为.
11. 如图,已知 , 若 , , , 则的长为. 12. 如图,点A在双曲线上,点B在双曲线上,且轴,点C、D在x轴上,若四边形为矩形,则它的面积为
12. 如图,点A在双曲线上,点B在双曲线上,且轴,点C、D在x轴上,若四边形为矩形,则它的面积为 13. 如图,在菱形中, , , E,F分别是边和对角线上的动点,且 , 则的最小值为.
13. 如图,在菱形中, , , E,F分别是边和对角线上的动点,且 , 则的最小值为.
三、解答题
-
14. 解方程:(x+4)2=5(x+4)15. 随着互联网的发展,人们的购物方式有了变化,使用网络平台在线购物越来越多.某产品今年开始做线上销售,8月份的销售利润是6万元,10月份的销售利润是13.5万元,求9,10这两个月销售利润的月平均增长率.16. 如图,在 中,请用尺规作图法,在 边上找一点 ,使 .(保留作图痕迹,不写作法)
 17. 如图,已知反比例函数与直线交于 , B两点.
17. 如图,已知反比例函数与直线交于 , B两点. (1)、求点B的坐标;(2)、根据函数图象,直接写出关于x的不等式的解集.18. 如图,点E是菱形ABCD的边BC延长线上一点,AC是对角线,∠BAC:∠ACE=2:7,求∠B的度数.
(1)、求点B的坐标;(2)、根据函数图象,直接写出关于x的不等式的解集.18. 如图,点E是菱形ABCD的边BC延长线上一点,AC是对角线,∠BAC:∠ACE=2:7,求∠B的度数. 19. 在平面直角坐标系中的位置如图所示,已知点 , , .与是以点P为位似中心的位似图形.
19. 在平面直角坐标系中的位置如图所示,已知点 , , .与是以点P为位似中心的位似图形.
( 1 )请画出点P的位置,并写出点P的坐标是____;
( 2 )以点O为位似中心,在y轴左侧画出△ABC的位似图形 , 使相似比为1:1.20. 如图,乐乐测得学校门口栏杆的短臂长1米,长臂长4米,当短臂外端A下降米时,求长臂外端B升高多少米? 21. 已知关于 的方程 .(1)、若该方程有两个不相等的实数根,求实数 的取值范围:(2)、当该方程的一个根为-3时,求 的值及方程的另一根.22. 在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
21. 已知关于 的方程 .(1)、若该方程有两个不相等的实数根,求实数 的取值范围:(2)、当该方程的一个根为-3时,求 的值及方程的另一根.22. 在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢. (1)、请用列表或画树状图的方法表示上述游戏中的所有可能结果.(2)、请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.23. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,其图象如下图所示所示.请根据图象中的信息解决下列问题:
(1)、请用列表或画树状图的方法表示上述游戏中的所有可能结果.(2)、请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.23. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,其图象如下图所示所示.请根据图象中的信息解决下列问题: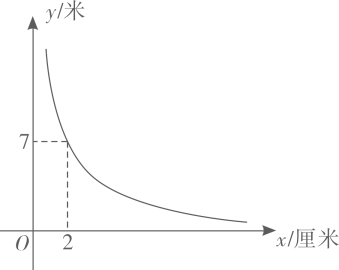 (1)、求y与x之间的函数表达式;(2)、当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为多少米?(3)、若某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是多少厘米?
(1)、求y与x之间的函数表达式;(2)、当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为多少米?(3)、若某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是多少厘米?