陕西省西安市经开区2022-2023学年八年级上学期期末质量检测数学试题

试卷更新日期：2023-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数2，0， $- 3$ ， $- \sqrt{2}$ 中，最小的数是（）

A、2 B、0 C、 $- 3$ D、 $- \sqrt{2}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{8} - \sqrt{2} = 2$ C、 $\sqrt{3} \times \sqrt{6} = 2 \sqrt{3}$ D、 $\sqrt{27} \div \sqrt{3} = 3$

查看试题解析
3. 下列画出的直线a与b不一定平行的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在围棋棋盘上有3枚棋子，如果黑棋①的位置用有序数对 $(0 ， - 1)$ 表示，黑棋②的位置用有序数对 $(- 3 ， 0)$ 表示，则白棋③的位置可用有序数对表示为（）

A、 $(2 ， 1)$ B、 $(- 1 ， 2)$ C、 $(- 2 ， 1)$ D、 $(1 ， - 2)$

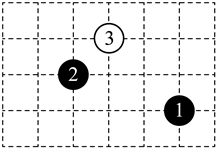查看试题解析
5. 地球的水资源越来越枯竭，全世界都提倡节约用水，小明把自己家1月至6月份的用水量绘制成折线图，那么小明家这6个月的月平均用水量是（　　）

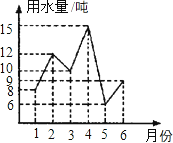A、10吨 B、9吨 C、8吨 D、7吨

查看试题解析
6. 在平面直角坐标系中，将直线 $y = - \frac{1}{2} x + 2$ 沿y轴向下平移5个单位后，得到一条新的直线，该新直线与x轴的交点坐标是（）

A、（0，-3） B、（-6，0） C、（4，0） D、（14，0）

查看试题解析
7. 若关于x，y的方程组 ${\begin{array}{l} x - y = 2 \\ m x + y = 6 \end{array}$ 有非负整数解，则正整数m为（）

A、 $1$ ， $7$ B、 $3$ ， $7$ C、1，3 D、 $1$ ， 3，7

查看试题解析
8. 如图， $△ A B C$ 的顶点A，B，C在边长为1的正方形网格的格点上，则 $B C$ 边上的高为（）

A、 $\frac{\sqrt{13}}{2}$ B、 $\frac{4 \sqrt{5}}{5}$ C、 $\frac{\sqrt{30}}{2}$ D、 $\frac{8 \sqrt{5}}{5}$

查看试题解析

二、填空题

9. $\sqrt{16}$ 的算术平方根是

查看试题解析
10. 为庆况神舟十五号发射成功，学校开展航天知识竞赛活动.经过几轮筛选，本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛，经过统计，四名同学成绩的平均数（单位：分）及方差（单位：分 $^{2}$ ）如表所示：

甲
乙
丙
丁
平均数
98
96
98
95
方差
0.4
2
1.6
0.4
若要选一名成绩好且状态稳定的同学参赛，那么应该选择.

查看试题解析
11. 已知正比例函数 $y = k x$ 的图象经过第二、四象限，若点 $A (1 ， a) ， B (- 1 ， b)$ 在该函数的图象上，则ab.（填“>”“<”或“=”）

查看试题解析
12. 如图，5个大小形状完全相同的长方形纸片，在直角坐标系中摆成如图图案，已知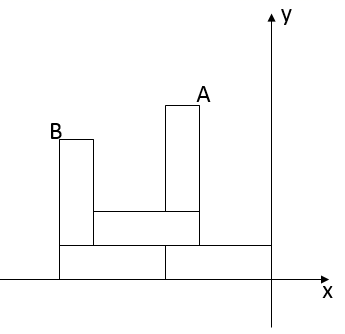 $B (- 8 ， 5)$ ，则点A的坐标为.

查看试题解析
13. 如图，台阶阶梯每一层高 $20 c m$ ，宽 $30 c m$ ，长 $50 c m$ ，一只蚂蚁从A点爬到B点，最短路程是 $c m$ ．

查看试题解析

三、解答题

14. 计算： $\sqrt[3]{- 27} + (- 3)^{0} - \sqrt{8} + | - 2 \sqrt{2} |$ .

查看试题解析
15. 解方程组： ${\begin{array}{l} 3 x + 2 y = 7 \\ 4 x - y = 13 \end{array}$

查看试题解析
16. 如图， $∠ B = 30 °$ ， $∠ C A D = 65 °$ ， $A D$ 平分 $∠ C A E$ ，求 $∠ A C D$ 的度数.

查看试题解析
17. 已知： $3 a + 1$ 的立方根是 $- 2 ， 3 \cdot 3^{b} \cdot 3^{2 b} = 81$ ， c是 $\sqrt{23}$ 的整数部分.

(1)、求a，b，c的值；

(2)、求 $2 a - b + 2 c$ 的平方根.

查看试题解析
18. 如图，在平面直角坐标系中，A（-3，2），B（-4，-3），C（-1，-1）是△ABC的顶点.

(1)、画出△ABC关于y轴的对称图形△A₁B₁C₁；

(2)、直接写出点C₁的坐标；

(3)、求AC₁的长.

查看试题解析
19. 《算法统宗》中记载着一首饮酒数学诗：“肆中饮客乱纷纷，薄酒名酶厚酒醇，醇酒一瓢醉三客，薄酒三瓶醉一人，共同饮了一十九，三十三客醉颜生，试问高明能算士，几多酶酒几多醇？”其意思是：醇酒1瓶，可以醉倒3位客人，薄酒3瓶，可以醉倒1位客人，如果33位客人醉倒了，那么他们总共饮下了19瓶酒，问饮下醇酒，薄酒分别多少瓶？

查看试题解析
20. 已知：如图，四边形ABCD中，∠ACB=90°，AB=15，BC=9，AD=5，DC=13，
求证：△ACD是直角三角形.

查看试题解析
21. 如图，已知 $A B ∥ C D$ ，射线 $A H$ 交 $B C$ 于点F，交 $C D$ 于点D，从点D引一条射线 $D E$ ，若 $∠ B + ∠ C D E = 180 °$ ，求证： $∠ A F C = ∠ E D H$ .

查看试题解析
22. 有这样一个问题：探究函数 $y = | x - 1 | - 2$ 的图象与性质.
乐乐根据学习一次函数的经验，对函数 $y = | x - 1 | - 2$ 的图象与性质进行了探究.
下面是乐乐的探究过程，请补充完整：

(1)、下表是x与y的几组对应值
x
…
$- 3$
$- 2$
$- 1$
0
1
2
3
4
…
y
…
2
m
0
$- 1$
$- 2$
$- 1$
0
1
…
m的值为；

(2)、在如图所示的平面直角坐标系中，描出上表中各组对应值为坐标的点，并画出该函数图象；

(3)、结合函数图象，写出该函数的两条性质.

查看试题解析
23. 阳光中学积极开展课后廷时服务话动，提供了“有趣的生物实验，虚拟机器人竞赛，国际象棋大赛，趣味篮球训练，经典影视欣赏……”等课程供学生自由选择一个学期后，该校为了解学生对课后延时服务的满意情况，随机对部分学生进行问卷调查，并将调查结果按照“A.非常满意；B.比较满意；C.基本满意；D.不满意”四个等级绘制成了如图所示的两幅不完整的统计图.

请根据图中信息，解答下列问题：

(1)、该校抽样调查的学生人数为人，请补全条形统计图；

(2)、样本中，学生对课后延时服务满意情况的“中位数”所在等级为， “众数”所在等级为；（填“A，B，C或D”）

(3)、若该校共有学生2000人，估计全校学生对课后延时服务满意的（包含A，B，C三个等级）有多少人？

查看试题解析
24. 如图，大拇指与小拇指尽量张开时，两指尖的距离称为“指距”，研究表明，一般情况下人的身高 $h (c m)$ 是指距 $d (c m)$ 的一次函数，
【测量数据】测量数据如表：
指距 $d (c m)$
20
21
22
23
身高 $h (c m)$
160
169
178
187

(1)、【关系探究】
根据表中数据，求h与d之间的函数关系式；

(2)、【结论应用】
我国篮球运动员周琦的身高约为 $217 c m$ ，估算他的指距是多少？（结果精确到 $0.1 c m$ ）

查看试题解析
25. 请解答下列各题：

(1)、阅读并回答：科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等．如图1，一束平行光线 $A B$ 与 $D E$ 射向一个水平镜面后被反射，此时 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．

①由条件可知： $∠ 1 = ∠ 3$ ，依据是， $∠ 2 = ∠ 4$ ，依据是．

②反射光线 $B C$ 与 $E F$ 平行，依据是．

(2)、解决问题：如图2，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射到平面镜 $b$ 上，又被 $b$ 镜反射，若 $b$ 射出的光线 $n$ 平行于 $m$ ，且 $∠ 1 = 42 °$ ，则 $∠ 2 =$ ； $∠ 3 =$ ．

查看试题解析
26. 如图，直线 $y = - 2 x + 12$ 与x轴交于点A，与y轴交于点B，与直线 $y = x$ 交于点C.

(1)、求点C的坐标；

(2)、在直线 $A B$ 上是否存在点M，使得 $S_{△ M O C} = 2 S_{△ A O C}$ ？若存在，请求出点M的坐标；若不存在，请说明理由.

查看试题解析

	甲	乙	丙	丁
平均数	98	96	98	95
方差	0.4	2	1.6	0.4

x	…	$- 3$	$- 2$	$- 1$	0	1	2	3	4	…
y	…	2	m	0	$- 1$	$- 2$	$- 1$	0	1	…

指距 $d (c m)$	20	21	22	23
身高 $h (c m)$	160	169	178	187