陕西省渭南市临渭区2022-2023学年度九年级上学期期末教学质量调研数学
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 如图所示的几何体,其主视图是( )
 A、
A、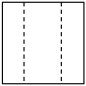 B、
B、 C、
C、 D、
D、 2. 如图,两条直线被三条平行线所截,已知AB=3,DE=4,EF=8,则AC的长是( )
2. 如图,两条直线被三条平行线所截,已知AB=3,DE=4,EF=8,则AC的长是( ) A、9 B、 C、 D、73. 已知反比例函数y=(k≠0)与正比例函数y=-2x没有交点,且双曲线图象上有三点A(-1,a)、B(-3,b)、C(4,c),则a、b、c的大小关系为( )A、a>b>c B、b>a>c C、c>b>a D、c>a>b4. 设是方程的两个实数根,则的值为( )A、 B、2018 C、 D、20225. 一个不透明的箱子里装有m个球,其中红球3个,这些球除颜色不同其余都相同,每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.3附近,则可以估算出m的值为( )A、3 B、5 C、10 D、126. 如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )
A、9 B、 C、 D、73. 已知反比例函数y=(k≠0)与正比例函数y=-2x没有交点,且双曲线图象上有三点A(-1,a)、B(-3,b)、C(4,c),则a、b、c的大小关系为( )A、a>b>c B、b>a>c C、c>b>a D、c>a>b4. 设是方程的两个实数根,则的值为( )A、 B、2018 C、 D、20225. 一个不透明的箱子里装有m个球,其中红球3个,这些球除颜色不同其余都相同,每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.3附近,则可以估算出m的值为( )A、3 B、5 C、10 D、126. 如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( ) A、2 B、4 C、8 D、167. 如图,已知菱形 的对角线 , 的长分别为6cm,8cm, 于点 ,则 的长是( )
A、2 B、4 C、8 D、167. 如图,已知菱形 的对角线 , 的长分别为6cm,8cm, 于点 ,则 的长是( ) A、 B、 C、 D、8. 如图,正方形中, , 点E在边上,且.将沿对折至 , 延长交于点G,连结.下列结论:①;②;③ ;④ .其中正确结论的个数是( )
A、 B、 C、 D、8. 如图,正方形中, , 点E在边上,且.将沿对折至 , 延长交于点G,连结.下列结论:①;②;③ ;④ .其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 已知点C是线段的黄金分割点,且 , , 则的长度是10. 我国南宋数学家杨辉在1275年提出一个问题:“直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.”意思是一块田是矩形,矩形面积为 , 长比宽多 , 如果设宽为 , 则列出的方程为.11. 如图是一个包装盒的三视图,则这个包装盒的体积是 .
 12. 如图,在平面直角坐标系中, , 点A坐标是 , 若反比例函数的图像经过点B,则k的值为.
12. 如图,在平面直角坐标系中, , 点A坐标是 , 若反比例函数的图像经过点B,则k的值为. 13. 如图,在矩形ABCD中,AB=5,AD=3,动点P满足3S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为.
13. 如图,在矩形ABCD中,AB=5,AD=3,动点P满足3S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为.
三、解答题
-
14. 用适当的方法解下列方程(1)、;(2)、.15. 先化简,再求值: ,其中 .16. 解方程: .17. 如图,已知Rt△ABC中∠C=90°,点D为AB边上一点,利用尺规作图的方法在AC上找一点 E,使得△ADE∽△ACB.
 18. 已知:如图,在菱形中,E.F分别是边和上的点,且 , 求证:.
18. 已知:如图,在菱形中,E.F分别是边和上的点,且 , 求证:. 19. 已知:关于x的一元二次方程 .
19. 已知:关于x的一元二次方程 .求证:此方程一定有实数根.
20. 如图,和是直立在地面上的两根立柱,已知 , 某一时刻在太阳光下的影子长. (1)、在图中画出此时在太阳光下的影子;(2)、在测量的影子长时,同时测量出 , 计算的长.21. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.22. 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
(1)、在图中画出此时在太阳光下的影子;(2)、在测量的影子长时,同时测量出 , 计算的长.21. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.22. 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB. 23. 2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行,冬奥会吉祥物为“冰墩墩”.
23. 2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行,冬奥会吉祥物为“冰墩墩”. (1)、据市场调研发现,某工厂今年二月份共生产500个“冰墩墩”,为增大生产量,该工厂平均每月生产量增长率相同,四月份该工厂生产了720个“冰墩墩”,求该工厂平均每月生产量增长率是多少?(2)、已知某商店“冰墩墩”平均每天可销售20个,每个盈利40元,在每个降价幅度不超过10元的情况下,每下降2元,则每天可多售10件.如果每天要盈利1440元,则每个“冰墩墩”应降价多少元?24. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,延长BC到点F,使CF=BE,连接DF.
(1)、据市场调研发现,某工厂今年二月份共生产500个“冰墩墩”,为增大生产量,该工厂平均每月生产量增长率相同,四月份该工厂生产了720个“冰墩墩”,求该工厂平均每月生产量增长率是多少?(2)、已知某商店“冰墩墩”平均每天可销售20个,每个盈利40元,在每个降价幅度不超过10元的情况下,每下降2元,则每天可多售10件.如果每天要盈利1440元,则每个“冰墩墩”应降价多少元?24. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,延长BC到点F,使CF=BE,连接DF.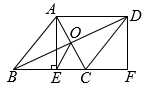 (1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.25. 一次函数与反比例函数()在第一象限内交于点D.
(1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.25. 一次函数与反比例函数()在第一象限内交于点D. (1)、求点D的坐标;(2)、若点P是y轴上一点,在平面内是否存在点Q,使得以D,E,P,Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.26.(1)、问题提出
(1)、求点D的坐标;(2)、若点P是y轴上一点,在平面内是否存在点Q,使得以D,E,P,Q为顶点的四边形是菱形?若存在,请求出点Q的坐标,若不存在,请说明理由.26.(1)、问题提出
如图1,在Rt△ABC中,∠ACB=90°,AC>BC,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC, PF⊥BC.垂足分别为E,F,则图1中四边形PECF的形状为. (2)、问题探究
(2)、问题探究
如图2,在Rt△ABC中,∠ACB=90°,AC=10,BC=6,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC,PF⊥BC.垂足分别为E,F,求四边形PECF的面积; (3)、问题解决
(3)、问题解决
如图3,△ABC是儿童公园内“少儿活动中心”的设计示意图.已知AB=80m,∠ACB=120°,∠ACB的平分线交AB于点P,过点P分别作PE⊥AC,PF⊥BC,垂足分别为E,F.按设计要求,四边形内部为室内活动区,阴影部分是室外活动区.若∠CAB=30°,求室内活动区PECF的面积.