海南省省直辖县级行政单位东方市2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 有理数的相反数是( )A、2 B、 C、 D、2. 为了加快构建清洁低碳、安全高效的能源体系,国家发布《关于促进新时代新能源高质量发展的实施方案》,旨在锚定到2030年我国风电、太阳能发电总装机容量达到1200000000千瓦以上的目标.数据1200000000用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的主视图是( )
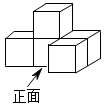 A、
A、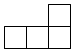 B、
B、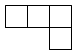 C、
C、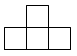 D、
D、 4. 实数9的平方根是( )A、3 B、±3 C、 D、815. 三角形三边分别是下列各组数,能组成直角三角形的是( )A、2,3,4 B、2,3,5 C、6,8,9 D、6,8,106. 下列各数中,是无理数的为( )A、 B、 C、 D、7. 下列计算正确的是( )A、 B、 C、 D、8. 若是一个完全平方式,那m的值是( )A、 B、 C、 D、9. 请估计应在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间10. 下列命题中是假命题的是( ).A、同旁内角互补,两直线平行 B、直线 , 则a与b相交所成的角为直角 C、如果两个角互补,那么这两个角是一个锐角,一个钝角 D、若 , , 那么11. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )
4. 实数9的平方根是( )A、3 B、±3 C、 D、815. 三角形三边分别是下列各组数,能组成直角三角形的是( )A、2,3,4 B、2,3,5 C、6,8,9 D、6,8,106. 下列各数中,是无理数的为( )A、 B、 C、 D、7. 下列计算正确的是( )A、 B、 C、 D、8. 若是一个完全平方式,那m的值是( )A、 B、 C、 D、9. 请估计应在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间10. 下列命题中是假命题的是( ).A、同旁内角互补,两直线平行 B、直线 , 则a与b相交所成的角为直角 C、如果两个角互补,那么这两个角是一个锐角,一个钝角 D、若 , , 那么11. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( ) A、6 B、7 C、8 D、912. 如图,在中, , 分别以点A、点B为圆心,大于的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若 , 则的度数是( ).
A、6 B、7 C、8 D、912. 如图,在中, , 分别以点A、点B为圆心,大于的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若 , 则的度数是( ).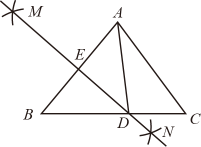 A、20° B、30° C、40° D、50°
A、20° B、30° C、40° D、50°二、填空题
-
13. 因式分解:.14. 计算:.15. 如图,一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前的高度是m.
 16. 如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接BE,发现AB=BE,若DE=1,则正方形ABCD的面积为.
16. 如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接BE,发现AB=BE,若DE=1,则正方形ABCD的面积为.
三、解答题
-
17. 计算:(1)、;(2)、解不等式组:.18. 如图,点在同一直线上, , 求证:.
 19. 若某中学生体质健康综合评定成绩为x分,满分为100分.规定:为A级,5为B级,为C级,为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
19. 若某中学生体质健康综合评定成绩为x分,满分为100分.规定:为A级,5为B级,为C级,为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
请根据图中的信息,解答下列问题:
(1)、在这次调查中,一共抽取了名学生;(2)、C等级的人数为人,a=%;(3)、D等级对应的圆心角为度.20. 如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.

