广西壮族自治区玉林市2022-2023学年七年级上学期期末数学试题
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 四个有理数 , 其中最小的是( )A、-2 B、-1 C、0 D、22. 若关于x的方程的解是 , 则a的值等于( )A、8 B、0 C、2 D、3. 单项式-5ab3的系数是( )A、5 B、-5 C、4 D、34. 某正方体的平面展开图如图所示,则原正方体中与“斗”字所在的面相对的面上的字是( )
 A、青 B、来 C、春 D、用5. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1056. 关于多项式3x2-y-3xy3+x5-1,下列说法错误的是( )A、这个多项式是五次五项式 B、常数项是-1 C、四次项的系数是3 D、按x降幂排列为x5+3x2-3xy3-y-17. 若方程 的解为-1,则 的值为( )A、10 B、-4 C、-6 D、-88.
A、青 B、来 C、春 D、用5. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1056. 关于多项式3x2-y-3xy3+x5-1,下列说法错误的是( )A、这个多项式是五次五项式 B、常数项是-1 C、四次项的系数是3 D、按x降幂排列为x5+3x2-3xy3-y-17. 若方程 的解为-1,则 的值为( )A、10 B、-4 C、-6 D、-88.将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
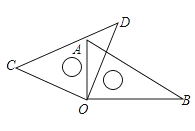 A、140° B、160° C、170° D、150°9. 在春节到来之际,某童装推出系列活动,一位妈妈看好两件衣服,她想给孩子都买下来作为新年礼物,与店员商量希望都以60元的价格卖给她.销售员发现这样一件就会盈利25%,另一件就会亏损25%,但是卖出这两件衣服总的是盈利还是亏损或是不盈不亏呢?请你用学过的知识帮着判断一下( )A、不盈不亏 B、盈利50元 C、盈利8元 D、亏损8元10. 如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC的度数是( )
A、140° B、160° C、170° D、150°9. 在春节到来之际,某童装推出系列活动,一位妈妈看好两件衣服,她想给孩子都买下来作为新年礼物,与店员商量希望都以60元的价格卖给她.销售员发现这样一件就会盈利25%,另一件就会亏损25%,但是卖出这两件衣服总的是盈利还是亏损或是不盈不亏呢?请你用学过的知识帮着判断一下( )A、不盈不亏 B、盈利50元 C、盈利8元 D、亏损8元10. 如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC的度数是( ) A、125° B、115° C、135° D、145°11. 有一个正方体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的点数是( )
A、125° B、115° C、135° D、145°11. 有一个正方体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的点数是( )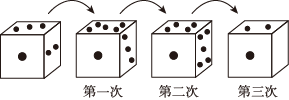 A、5 B、3 C、4 D、212. 将一张正方形纸片按如图所示的方式折叠,、为折痕,点折叠后的对应点分别为 , 若 , 则的度数为( )
A、5 B、3 C、4 D、212. 将一张正方形纸片按如图所示的方式折叠,、为折痕,点折叠后的对应点分别为 , 若 , 则的度数为( ) A、48° B、46° C、44° D、42°
A、48° B、46° C、44° D、42°二、填空题
-
13. 某市今年元旦的最低气温为 , 最高气温为 , 这天的最高气温比最低气温高℃.14. °.15. 多项式 加上一个单项式后所得的和是一个二次二项式,则这个单项式可以是 .(填一个即可)16. 一般情况下+=不成立,但有数可以使得它成立.例如a=b=0.我们称使得+= 成立的一对数a、b为“相伴数对”,记为(a,b).若(a,2)为“相伴数对”,则a的值为.17. 一件工程甲单独做50天可完成,乙单独做75天可完成,现在两个人合作.但是中途乙因事离开几天,从开工后40天把这件工程做完.则乙中途离开了天.18. 历史上数学家欧拉最先把关于x的多项式用记号来表示,把x等于某数a时的多项式的值用来表示.例如,对于多项式 , 当时,多项式的值为.若对于多项式 , 有 , 则的值为.
三、解答题
-
19. 计算:(1)、;(2)、.20. 解下列方程:(1)、;(2)、.21. 先化简,再求值:6xy2-4x2y-3(xy2-x2y),其中x=2,y=-1.22. 如图,已知线段AB,请按要求完成下列问题.
 (1)、用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;(2)、如果AB=2cm;
(1)、用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;(2)、如果AB=2cm;①求CD的长度;
②设点P是线段BD的中点,求线段CP的长度.
23. 如图,点 在同一条直线上,射线 和射线 分别平分 和 ,若 ,求 及 的度数.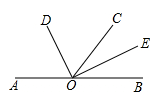 24. 我们规定,若关于x的一元一次方程ax=b的解为b﹣a,则称该方程为“差解方程”,例如:2x=4的解为2,且2=4﹣2,则该方程2x=4是差解方程.(1)、判断3x=4.5是否是差解方程;(2)、若关于x的一元一次方程5x=m+1是差解方程,求m的值.25. 某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
24. 我们规定,若关于x的一元一次方程ax=b的解为b﹣a,则称该方程为“差解方程”,例如:2x=4的解为2,且2=4﹣2,则该方程2x=4是差解方程.(1)、判断3x=4.5是否是差解方程;(2)、若关于x的一元一次方程5x=m+1是差解方程,求m的值.25. 某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:用水量/月
单价(元/)
不超过
超过的部分
另:每立方米用水加收元的城市污水处理费和元的城市附加费
(1)、根据上表,用水量每月不超过 , 实际每立方米收水费多少元?如果10月份某用户用水量为 , 那么该用户10月份应该缴纳水费多少元?(2)、某用户11月份共缴纳水费80元,那么该用户11月份用水多少?(3)、若该用户水表12月份出了故障,有25%的水量没有计入水表中,这样该用户在12月份只缴纳了54元水费,问该用户12月份实际应该缴纳水费多少元?26. 已知O为直线上一点,射线位于直线上方,在的左侧,.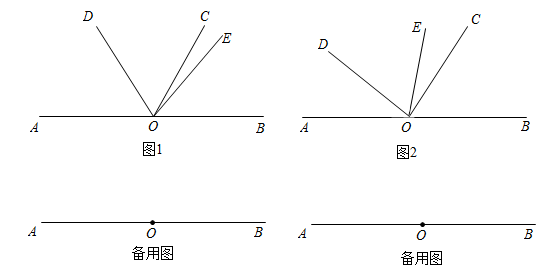 (1)、如图1, , 当平分时,求的度数.(2)、如图2,若 , 且 , 求的度数(用含的代数式表示);(3)、若 , 点F在射线上,若射线绕点O顺时针旋转平分 , 当时,求n的值.
(1)、如图1, , 当平分时,求的度数.(2)、如图2,若 , 且 , 求的度数(用含的代数式表示);(3)、若 , 点F在射线上,若射线绕点O顺时针旋转平分 , 当时,求n的值.