广西壮族自治区南宁市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 2022年12月4日,神舟十四号载人飞船返回舱在东风着陆场成功着陆,本次载人飞行任务取得圆满成功,下列航天图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程的二次项系数是( )A、 B、 C、 D、3. 如图,在中, , 则度数为( )
2. 一元二次方程的二次项系数是( )A、 B、 C、 D、3. 如图,在中, , 则度数为( ) A、 B、 C、 D、4. 已知一元二次方程的一个根是1,则b的值是( )A、 B、 C、 D、5. 抛物线向下平移一个单位得到抛物线( )A、 B、 C、 D、6. 一个不透明的盒子中装有2个白球,1个红球和1个黄球,这些球除了颜色外无其他差别,若从盒子中随机摸出一个球,则摸到红球的概率是( )A、 B、 C、 D、17. 二次函数的图象与y轴的交点坐标是( )A、 B、 C、 D、8. 以原点为中心,把点逆时针旋转90°得到点B,则点B的坐标为( )A、 B、 C、 D、9. 已知抛物线与x交于点 , , 则关于x的方程的解是( )A、 , B、 , C、 , D、 ,10. 如图,是的直径,弦于点E,连接 , 若 , , 则弦的长是( )
A、 B、 C、 D、4. 已知一元二次方程的一个根是1,则b的值是( )A、 B、 C、 D、5. 抛物线向下平移一个单位得到抛物线( )A、 B、 C、 D、6. 一个不透明的盒子中装有2个白球,1个红球和1个黄球,这些球除了颜色外无其他差别,若从盒子中随机摸出一个球,则摸到红球的概率是( )A、 B、 C、 D、17. 二次函数的图象与y轴的交点坐标是( )A、 B、 C、 D、8. 以原点为中心,把点逆时针旋转90°得到点B,则点B的坐标为( )A、 B、 C、 D、9. 已知抛物线与x交于点 , , 则关于x的方程的解是( )A、 , B、 , C、 , D、 ,10. 如图,是的直径,弦于点E,连接 , 若 , , 则弦的长是( ) A、 B、 C、 D、11. 某公司2017年的营业额是100万元,2019年的营业额为121万元,设该公司年营业额的平均增长率为 ,根据题意可列方程为( )A、 B、 C、 D、12. 如图1,在平面内选一定点O,引一条有方向的射线 , 再选定一个单位长度,那么平面上任意一点M的位置可由的长度m与的度数确定,有序数对称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
A、 B、 C、 D、11. 某公司2017年的营业额是100万元,2019年的营业额为121万元,设该公司年营业额的平均增长率为 ,根据题意可列方程为( )A、 B、 C、 D、12. 如图1,在平面内选一定点O,引一条有方向的射线 , 再选定一个单位长度,那么平面上任意一点M的位置可由的长度m与的度数确定,有序数对称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图2的极坐标系下,如果与相切于点B, , 射线与交于C,D两点,连接 , , 则点D的极坐标应记为( )
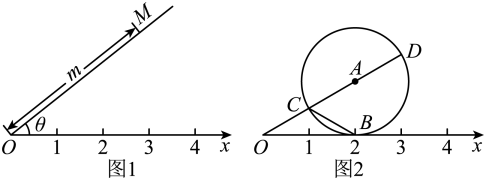 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若二次函数的图象开口向上,则a的取值范围是.14. 的半径是 , 点P与圆心O的距离是 , 则点在.(填写“内”、“上”、“外”)15. 关于x的方程有两个相等的实数根,则m的值是.16. 为了解某花卉种子的发芽情况,研究所工作人员在相同条件下,对该花卉种子进行发芽试验,相关数据记录如下:
种子总数
100
400
800
1400
3500
7000
发芽种子数
91
358
724
1264
3160
6400
发芽的频率
0.91
0.895
0.905
0.903
0.903
0.914
根据以上数据,可以估计该花卉种发芽的概率为(结果精确到0.1).
17. 如图,在中, , , , 将绕点A顺时针旋转得到 , 使点在的延长线上,则的长为. 18. 如图,在中, , , 以为直径作 , 交斜边于点C,点D在直径右侧的半圆上,且 , 连接 , 则的长度为.
18. 如图,在中, , , 以为直径作 , 交斜边于点C,点D在直径右侧的半圆上,且 , 连接 , 则的长度为.
三、解答题
-
19. 计算:.20. 解方程: .21. 如图,已知点A的坐标为 , 点B的坐标为.
 (1)、作出关于原点对称的;(2)、请判断四边形的形状,并证明你的结论.22. 第二十二届世界杯足球赛在卡塔尔举行,这是历史上首次在中东国家境内举行,也是首次在北半球冬季举行,共32支球队拥有该届世界杯决赛圈的参赛资格.(1)、这届世界杯冠军从这32支球队中产生是事件;(“必然”,“随机”,“不可能”)(2)、学校为了让同学们更多的了解世界杯,举办了与其相关的知识竞赛,七年级的甲、乙、丙、丁四名同学表现优秀,其中甲、乙来自一班,丙、丁来自二班,若从这四名同学中随机抽取两名同学参加全校比赛,求两名同学均来自二班的概率.23. 如图,将矩形绕点B旋转得到矩形 , 点E在上,延长交于点H.
(1)、作出关于原点对称的;(2)、请判断四边形的形状,并证明你的结论.22. 第二十二届世界杯足球赛在卡塔尔举行,这是历史上首次在中东国家境内举行,也是首次在北半球冬季举行,共32支球队拥有该届世界杯决赛圈的参赛资格.(1)、这届世界杯冠军从这32支球队中产生是事件;(“必然”,“随机”,“不可能”)(2)、学校为了让同学们更多的了解世界杯,举办了与其相关的知识竞赛,七年级的甲、乙、丙、丁四名同学表现优秀,其中甲、乙来自一班,丙、丁来自二班,若从这四名同学中随机抽取两名同学参加全校比赛,求两名同学均来自二班的概率.23. 如图,将矩形绕点B旋转得到矩形 , 点E在上,延长交于点H. (1)、求证:;(2)、连接 , 若 , 求的度数.24. 掷实心球是南宁市中考体育考试的项目.如图是一名女生掷实心球,实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图2所示,掷出时起点处高度为 , 当水平距离为时,实心球行进至最高点,此时距离地面.
(1)、求证:;(2)、连接 , 若 , 求的度数.24. 掷实心球是南宁市中考体育考试的项目.如图是一名女生掷实心球,实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图2所示,掷出时起点处高度为 , 当水平距离为时,实心球行进至最高点,此时距离地面. (1)、求y关于x的函数表达式;(2)、南宁市体育中考评分标准(女生)如下表所示:
(1)、求y关于x的函数表达式;(2)、南宁市体育中考评分标准(女生)如下表所示:成绩(分)
1
2
3
4
5
6
7
8
9
10
距离(米)
1.95
2.20
2.45
2.70
2.95
3.20
3.45
3.70
3.95
4.20
成绩(分)
11
12
13
14
15
16
17
18
19
20
距离(米)
4.70
5.10
5.50
5.90
6.30
6.70
7.10
7.50
7.90
8.30
该女生在此项考试中获得多少分,请说明理由.
25. 综合与实践问题情境:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l,圆心角为的扇形.工人在制作圆锥形物品时,通常要先确定扇形圆心角度数,再度量裁剪材料.
 (1)、探索尝试:图1中,圆锥底面周长与其侧面展开图的弧长;(填“相等”或“不相等”)若 , , 则n=.(2)、解决问题:为操作简便,工人希望能简洁求n的值,请用含r,l的式子表示n;(3)、拓展延伸:图2是一种纸质圆锥形生日帽, , , C是中点,现要从点A到点C再到点A之间拉一装饰彩带,求彩带长度的最小值.26. 如图,在平面直角坐标系中,直线交x轴于点B,交y轴于点C,直线交x轴于点A,交y轴于点D,交直线于点 , 且.
(1)、探索尝试:图1中,圆锥底面周长与其侧面展开图的弧长;(填“相等”或“不相等”)若 , , 则n=.(2)、解决问题:为操作简便,工人希望能简洁求n的值,请用含r,l的式子表示n;(3)、拓展延伸:图2是一种纸质圆锥形生日帽, , , C是中点,现要从点A到点C再到点A之间拉一装饰彩带,求彩带长度的最小值.26. 如图,在平面直角坐标系中,直线交x轴于点B,交y轴于点C,直线交x轴于点A,交y轴于点D,交直线于点 , 且. (1)、求直线AD解析式;(2)、点P从B点出发沿线段BA方向以1个单位/秒的速度向终点A运动(点P不与A,B两点重合),设点P的运动时间为t,则是否存在t,使得为等腰直角三角形?若存在,请求出t的值,若不存在,请说明理由;(3)、在(2)的条件下,点P出发的同时,点Q从C点出发沿射线CO方向运动,当点P到达终点时,点Q也停止运动,连接 , , 设的面积为S,S与t的函数关系式为 , 其图像如图2所示,结合图1、图2的信息,请求出a的值及当的面积取得最大值时的长.
(1)、求直线AD解析式;(2)、点P从B点出发沿线段BA方向以1个单位/秒的速度向终点A运动(点P不与A,B两点重合),设点P的运动时间为t,则是否存在t,使得为等腰直角三角形?若存在,请求出t的值,若不存在,请说明理由;(3)、在(2)的条件下,点P出发的同时,点Q从C点出发沿射线CO方向运动,当点P到达终点时,点Q也停止运动,连接 , , 设的面积为S,S与t的函数关系式为 , 其图像如图2所示,结合图1、图2的信息,请求出a的值及当的面积取得最大值时的长.