广西壮族自治区贵港市桂平市2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个数中，最大的数是（）

A、 $- 3$ B、 $- 1$ C、0 D、2

查看试题解析
2. 下列各线段的表示方法中，正确的是（）

A、线段A B、线段ab C、线段AB D、线段Ab

查看试题解析
3. 下列运算中，正确的是（）

A、 $2 (a - b) = 2 a - 1$ B、 $3 a^{2} b - 2 a^{2} b = a^{2} b$ C、 $a^{2} + a^{2} = a^{4}$ D、 $3 x + 2 y = 5 x y$

查看试题解析
4. 下列方程的变形，正确的是（）.

A、由 $5 + x = 1$ ，得 $x = 5 + 1$ B、由 $7 x = - 4$ ，得 $x = - \frac{7}{4}$ C、由 $\frac{1}{4} y = 0$ ，得 $y = 4$ D、由 $2 x + 5 = - 1$ ，得 $2 x = - 1 - 5$

查看试题解析
5. 在墙壁上固定一根横放的木条，则至少需要钉子的枚数是（　　）

A、1枚 B、2枚 C、3枚 D、任意枚

查看试题解析
6. 以下调查中，最适合采用全面调查的是（）

A、检测长征运载火箭的零部件质量情况 B、了解全国中小学生课外阅读情况 C、调查某批次汽车的抗撞击能力 D、检测某城市的空气质量

查看试题解析
7. 单项式 $π r^{2} h$ 的次数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图所示，点O为直线 $A B$ 上一点， $O D$ 平分 $∠ C O B$ ， $∠ A O C = 118 °$ .则 $∠ C O D$ 的度数是（）

A、 $26 °$ B、 $30 °$ C、 $31 °$ D、 $41 °$

查看试题解析
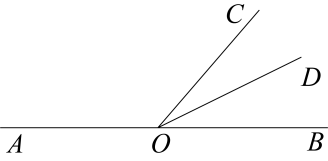9. 已知数a，b在数轴上表示的点的位置如图所示，则下列结论正确的是（）

A、 $a + b > 0$ B、 $a - b > 0$ C、 $- a > - b > a$ D、 $a \cdot b > 0$

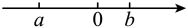查看试题解析
10. （古代数学问题）今有共买物，人出八，盈三；人出七，不足四.问人数、物价各几何？意思是：几个人一起去购买某物品，如果每人出8元，则多了3元；如果每人出7元，则少了4元，问有多少人，物品的价格是多少？（）

A、6人，52元 B、5人，37元 C、8人，60元 D、7人，53元

查看试题解析
11. 幻方是相当古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫图.将数字1，2，3，4，5，6，7，8，9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则 $m$ 的值为（    ）



   3

   8

   5

   m

A、6 B、2 C、1 D、4

查看试题解析
12. 【阅读理解】计算：25×11＝275，13×11＝143，48×11＝528，74×11＝814，观察算式，我们发现两位乘11的速算方法：头尾一拉，中间相加，满十进一.
【拓展应用】已知一个两位数，十位上的数字是a，个位上的数字是b，这个两位数乘11，计算结果的十位上的数字可表示为（　　）

A、a或a＋1 B、a＋b或ab C、a＋b−10 D、a＋b或a＋b−10

查看试题解析

二、填空题

13. 0的相反数是．

查看试题解析
14. 地球的表面积约为 $511000000 k m^{2}$ ，数据 $511000000$ 用科学记数法表示是.

查看试题解析
15. 一个角的补角加上30°后，等于这个角的余角的3倍，则这个角度数是.

查看试题解析
16. 已知 $x^{m - 1} - 2 = 0$ 是关于x的一元一次方程，则m的值是.

查看试题解析
17. 已知线段AB＝16，AM＝ $\frac{1}{3}$ BM，点P、Q分别是AM、AB的中点，当点M在直线AB上时，则PQ的长为.

查看试题解析
18. 已知整数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， …满足下列条件： $a_{1} = 0$ ， $a_{2} = - | a_{1} + 1 |$ ， $a_{3} = - | a_{2} + 2 |$ ， $a_{4} = - | a_{3} + 3 |$ ，以此类推，则 $a_{2022}$ 的值为.

查看试题解析

三、解答题

19. 计算：

(1)、 $- 56 \div 28 - (- 2) \times 5$

(2)、 $- 2^{4} - \frac{1}{7} \times [2 - {(- 3)}^{2}]$

查看试题解析
20. 先化简，再求值： $(4 x^{2} - x y + y^{2}) - 3 (x^{2} - x y + 5 y^{2})$ ，其中 $x = - 1$ ， $y = - \frac{1}{2}$ .

查看试题解析
21. 解方程：

(1)、 $5 (y + 8) - 5 = 6 (2 y - 7)$

(2)、 $\frac{x + 2}{4} - \frac{2 x - 3}{6} = 1$

查看试题解析
22. 如图，在平面内有三个点 $A$ ， $B$ ， $C$ ．

(1)、按下面的要求作图：（要求：利用尺规，不写画法，保留作图痕迹，不写结论）
①连接 $A B$ ， $A C$ ，作射线 $B C$ ；

②在射线 $B C$ 上作线段 $B D$ ，使 $B D = B C + A B$ ．

(2)、已知 $A B = 6$ ， $B C = 4$ ，点 $P$ 是 $B D$ 的中点．将点 $P$ 标在（1）所画的图中，并求线段 $C P$ 的长．

查看试题解析

23. 近年来，我市香蕉产业不断做大做强，打造出“洛洛香”、“甜弯弯”等优质品业牌.如今又到了香蕉上市的季节，某商家以每箱60元的进价购入200箱香蕉，然后分批全部卖出.售价以每箱75元为标准，超过的部分记为正，低于的部分记为负，记录如下：

超出标准（单位：元）	$+ 15$	$+ 12$	$+ 10$	0	$- 8$	$- 5$
卖出数量（单位：箱）	50	20	40	30	30	30

(1)、求每箱香蕉的平均售价是多少元？

(2)、该商家卖完所有香蕉所获利润为多少元？

查看试题解析

24. 某教学学习小组对“人们了解国家大事的途径”进行调查.

(1)、针对调查对象的选取设计了以下三种方案，你认为设计比较科学的是.
①到某一社区随机发放问卷；
②到人流量大的街上随机发放问卷；
③分别选取城市、乡村学校利用学校家长会随机对不同学历的人发放问卷.

(2)、将收集到的有效问卷进行整理，制成了不完整的扇形统计图和条形统计图如下：
①这次调查收回的有效问卷有，扇形统计图中m的值为；

②补全条形统计图；
③若样本总体数为 $1800$ 人，请你估计有多少人是通过“与人聊天”的途径了解国家大事的.

查看试题解析
25. 为鼓励节约用电，某地用电收费标准规定：如果每月每户用电不超过150度，那么每度电0.5元；如果该月用电超过150度，那么超过部分每度电0.8元.

(1)、如果小张家一个月用电128度，那么这个月应缴纳电费多少元？

(2)、如果小张家一个月用电a度，那么这个月应缴纳电费多少元？（用含a的代数式表示）

(3)、如果这个月缴纳电费为147.8元，那么小张家这个月用电多少度？

查看试题解析
26. 如图，已知∠AOB＝120°，OC是∠AOB内的一条射线，且∠AOC：∠BOC＝1：2．

(1)、求∠AOC，∠BOC的度数；

(2)、作射线OM平分∠AOC，在∠BOC内作射线ON，使得∠CON：∠BON＝1：3，求∠MON的度数；

(3)、过点O作射线OD，若2∠AOD＝3∠BOD，求∠COD的度数．

查看试题解析