广西壮族自治区贵港市桂平市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 函数 , 自变量x的取值范围是( )A、 B、 C、取任意实数 D、的一切实数2. 如图是一个几何体的主视图,则该几何体是( )
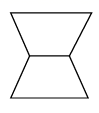 A、
A、 B、
B、 C、
C、 D、
D、 3. 对于函数的图像,下列说法不正确的是( )A、开口向下 B、对称轴是 C、最大值为0 D、与y轴不相交4. 已知一组数据:3,4,5,6,5,7.那么这组数据的方差是( )A、 B、 C、 D、5. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、6. 如图, 的半径 为 , 于点 , ,则 的长是( )
3. 对于函数的图像,下列说法不正确的是( )A、开口向下 B、对称轴是 C、最大值为0 D、与y轴不相交4. 已知一组数据:3,4,5,6,5,7.那么这组数据的方差是( )A、 B、 C、 D、5. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、6. 如图, 的半径 为 , 于点 , ,则 的长是( ) A、 B、 C、2 D、37. 一元二次方程 的根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定8. 如图,某超市电梯的截面图中,的长为15米,与的夹角为 , 则高是( )
A、 B、 C、2 D、37. 一元二次方程 的根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定8. 如图,某超市电梯的截面图中,的长为15米,与的夹角为 , 则高是( )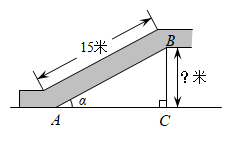 A、米 B、米 C、米 D、米9. 学校计划在长为12m,宽为9m矩形地块的正中间建一座劳动实践大棚.大棚是占地面积为88m2的矩形.建成后,大棚外围留下宽度都相同的区域,这个宽度应设计为( )
A、米 B、米 C、米 D、米9. 学校计划在长为12m,宽为9m矩形地块的正中间建一座劳动实践大棚.大棚是占地面积为88m2的矩形.建成后,大棚外围留下宽度都相同的区域,这个宽度应设计为( ) A、1.8m B、1.5m C、1m D、0.5m10. 如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )
A、1.8m B、1.5m C、1m D、0.5m10. 如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )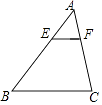 A、16 B、18 C、20 D、2411. 如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为( )
A、16 B、18 C、20 D、2411. 如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为( ) A、 B、 C、2 D、212. 已知二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系内的图象可能是( )
A、 B、 C、2 D、212. 已知二次函数的图象如图所示,则反比例函数与一次函数在同一平面直角坐标系内的图象可能是( ) A、
A、 B、
B、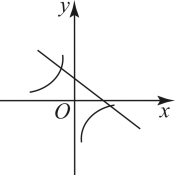 C、
C、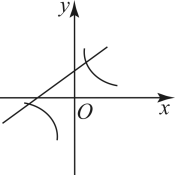 D、
D、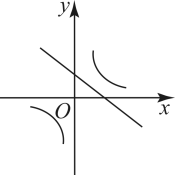
二、填空题
-
13. sin30°的值为 .14. 二次函数的顶点坐标是.15. 某市教育局为了解该市2.5万名九年级学生的身体素质情况,随机抽取了1000名九年级学生进行检测.已知被检测学生的身体素质达标率为 , 请据此估计该市九年级学生中身体素质达标的学生人数是人.16. 若m是方程的一个根,则的值为.17. 如图,已知扇形中, , 以为直径作半圆O,过点O作的平行线,分别交半圆O,弧于点 , 若扇形的半径为8,则图中阴影部分的面积是.
 18. 如图,抛物线与x轴正半轴交于两点,y轴负半轴交于点C.若点 , 则下列结论中: ;;与是抛物线上两点,若 , 则;若抛物线的对称轴是直线 , m为任意实数,则;若则其中正确结论的个数共有个.
18. 如图,抛物线与x轴正半轴交于两点,y轴负半轴交于点C.若点 , 则下列结论中: ;;与是抛物线上两点,若 , 则;若抛物线的对称轴是直线 , m为任意实数,则;若则其中正确结论的个数共有个.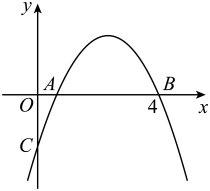
三、解答题
-
19. 计算:|﹣4|+3tan60°﹣ ﹣( )﹣120. 解方程:21. 如图,在四边形ABCD中,已知 , AE平分∠BAC,且 , .
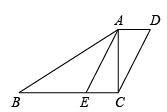 (1)、求证:;(2)、尺规作图:过点E作垂线 , 垂足为F(不要求写作法,保留作图痕迹);(3)、在(2)的条件下,已知四边形AECD面积为12, , 直接写出线段EF的长.22. 《城镇污水处理厂污染物排放标准》中硫化物的排放标准为.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为;从第60小时开始,所排污水中硫化物的浓度是监测时间x(小时)的反比例函数,其图象如图所示.
(1)、求证:;(2)、尺规作图:过点E作垂线 , 垂足为F(不要求写作法,保留作图痕迹);(3)、在(2)的条件下,已知四边形AECD面积为12, , 直接写出线段EF的长.22. 《城镇污水处理厂污染物排放标准》中硫化物的排放标准为.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为;从第60小时开始,所排污水中硫化物的浓度是监测时间x(小时)的反比例函数,其图象如图所示.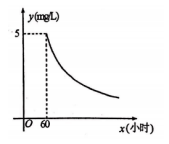 (1)、求y与x的函数关系式;(2)、整改开始第100小时时,所排污水中硫化物浓度为;(3)、按规定所排污水中硫化物的浓度不超过时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?23. 广州市某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
(1)、求y与x的函数关系式;(2)、整改开始第100小时时,所排污水中硫化物浓度为;(3)、按规定所排污水中硫化物的浓度不超过时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?23. 广州市某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:等级
非常了解
比较了解
基本了解
不太了解
频数
40
120
36
4
频率
0.2
m
0.18
0.02
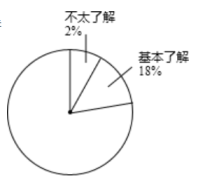 (1)、本次问卷调查抽取的样本容量为;表中m的值;(2)、根据表中数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数,并补全该扇形统计图;(3)、若该校有1500名学生,请根据调查结果,估算这些学生中“比较了解”垃圾分类知识的人数约有多少.24. 如图,在中, , 以为直径作 , 交于点D,过点D作 , 垂足为点E,交的延长线于点F.
(1)、本次问卷调查抽取的样本容量为;表中m的值;(2)、根据表中数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数,并补全该扇形统计图;(3)、若该校有1500名学生,请根据调查结果,估算这些学生中“比较了解”垃圾分类知识的人数约有多少.24. 如图,在中, , 以为直径作 , 交于点D,过点D作 , 垂足为点E,交的延长线于点F.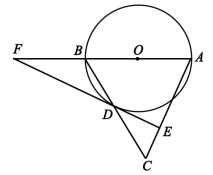 (1)、求证:是的切线;(2)、若的半径为5, , 求的长.25. 如图,在平面直角坐标系中,抛物线与x轴交于 , 两点,与y轴交于点C,点D是该抛物线的顶点.
(1)、求证:是的切线;(2)、若的半径为5, , 求的长.25. 如图,在平面直角坐标系中,抛物线与x轴交于 , 两点,与y轴交于点C,点D是该抛物线的顶点.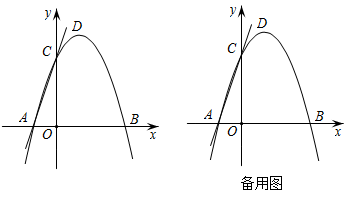 (1)、求抛物线的表达式;(2)、请在y轴上找一点M,使的周长最小,求出点M的坐标;(3)、试探究:在抛物线上是否存在点P,使以点为顶点,为直角边的三角形是直角三角形?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.26. 综合与时间
(1)、求抛物线的表达式;(2)、请在y轴上找一点M,使的周长最小,求出点M的坐标;(3)、试探究:在抛物线上是否存在点P,使以点为顶点,为直角边的三角形是直角三角形?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.26. 综合与时间问题情境:如图1,在正方形ABCD中,点E是对角线AC上一点,连接BE,过点E分别作AC,BE的垂线,分别交直线BC,CD于点F,G.试猜想线段BF和CG的数量关系,并加以证明.
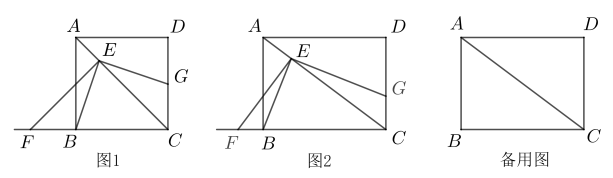 (1)、数学思考:请解答上述问题.(2)、问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若 , , 求的值.(3)、问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积.
(1)、数学思考:请解答上述问题.(2)、问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若 , , 求的值.(3)、问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积.