广西壮族自治区贵港市桂平市2022-2023学年八年级上期末数学试题
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 若分式的值等于0,则x的取值可以是( )A、0 B、 C、 D、12. 下列实数是无理数的是( )A、1 B、0 C、 D、3. 长度分别为a,2,4的三条线段能组成一个三角形,则a的值可能是( ).
A、1 B、2 C、3 D、64. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、5. 下列运算结果正确的是( )A、 B、 C、 D、6. 下列命题是真命题的是( )A、的值是 B、没有立方根 C、是有理数 D、实数分为正实数、负实数7. 若 , 则下列不等式正确的是( )A、 B、 C、 D、8. 在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )A、32° B、36° C、40° D、128°9. 一项工程,甲队独做要x天,乙队独做要y天,若甲乙两队合作,所需天数为( )A、 B、 C、 D、10. 已知m,n为两个连续的整数,且 , 则的值是( )A、2023 B、 C、1 D、11. 如果关于x的方程的解是正数,那么m的取值范围是( )A、 B、且 C、 D、且12. 已知是边长为10的等边三角形,为的中点, , 交线段于 , 交的延长线于.若 , 则的长为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 若二次根式 有意义,则x的取值范围是 .14. 可乐和奶茶含有大量的咖啡因,世界卫生组织建议青少年每天摄入的咖啡因不能超过0.000085kg,将数据0.000085用科学记数法表示为.15. 用不等式表示:“x的2倍与1的差小于3”是.16. 若 ,则 的值是.17. 如图,等边三角形 , , 点D,E,F分别是 , , 的中点,点P是线段上的一动点,连接 , , 则周长的最小值是.
 18. 对于两个不相等的实数a,b,我们规定符号表示a,b中的较小的值,如 , 按照这个规定,方程(其中)的解为.
18. 对于两个不相等的实数a,b,我们规定符号表示a,b中的较小的值,如 , 按照这个规定,方程(其中)的解为.三、解答题
-
19. 计算:.20.(1)、解方程:.(2)、解不等式组: , 并利用数轴确定不等式组的解集.21. 先化简,再求值: , 其中.22. 如图,四边形中, , , 连接.
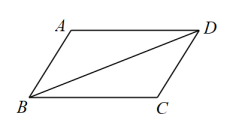 (1)、求证:;(2)、尺规作图(不写作法,保留作图痕迹):作的垂直平分线 , 分别交 , 于点E,F;(3)、连接 , 若 , 求的度数.23. [阅读材料]
(1)、求证:;(2)、尺规作图(不写作法,保留作图痕迹):作的垂直平分线 , 分别交 , 于点E,F;(3)、连接 , 若 , 求的度数.23. [阅读材料]我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,为三角形和多边形的面积计算提供了新的方法和思路,在知道三角形三边的长而不知道高的情况下使用秦九韶公式可以更简便地求出面积,比如说在测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地求出答案,即三角形的三边长分别为a、b、c,则其面积S=(秦九韶公式),此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a、b、c,记p= , 则其面积S=(海伦公式),虽然这两个公式形式上有所不同,但它们本质是等价的,计算各有优劣,它填补了中国数学史中的一个空白,从中可以看出中国古代已经具有很高的数学水平.
[解决问题]
(1)、当三角形的三边a=7,b=8,c=9时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.(2)、当三角形的三边a= , b=2 , c=3时,请你从上面两个公式里,选择合适的公式计算出三角形的面积.24. 等面积法是一种常用的、重要的数学解题方法. (1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.25. 2020年6月1日,随着《山西省城市生活垃圾分类管理规定》的实施,我省的生活垃圾分类工作正式进入“提速”模式,太原市各社区积极行动.某小区准备购买A , B两种分类垃圾桶,通过市场调研得知:A种垃圾桶每组的价格比B种垃圾桶每组的价格少120元,且用8000元购买A种垃圾桶的数量与用10400元购买B种垃圾桶的数量相等.
(1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.25. 2020年6月1日,随着《山西省城市生活垃圾分类管理规定》的实施,我省的生活垃圾分类工作正式进入“提速”模式,太原市各社区积极行动.某小区准备购买A , B两种分类垃圾桶,通过市场调研得知:A种垃圾桶每组的价格比B种垃圾桶每组的价格少120元,且用8000元购买A种垃圾桶的数量与用10400元购买B种垃圾桶的数量相等. (1)、求A , B两种垃圾桶每组的单价;(2)、该小区物业计划用不超过18000元的资金购买A , B两种垃圾桶共40组.则最多可以购买B种垃圾桶多少组?26. 如图,已知点D是等边三角形中边所在直线上的点,连接 , 过点D作 , 与的邻补角的平分线交于点F.
(1)、求A , B两种垃圾桶每组的单价;(2)、该小区物业计划用不超过18000元的资金购买A , B两种垃圾桶共40组.则最多可以购买B种垃圾桶多少组?26. 如图,已知点D是等边三角形中边所在直线上的点,连接 , 过点D作 , 与的邻补角的平分线交于点F.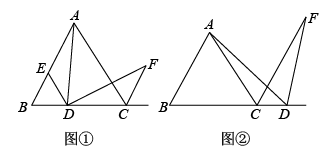 (1)、如图①,当点D在线段上时,过点D作 , 且交于点E.求证:;(2)、如图①,在(1)的条件下,求证:;(3)、如图②,当点D在线段的延长线上时,(2)中线段 , , 之间的数量关系式还成立吗?若成立,请加以证明;若不成立,请写出线段 , , 之间新的数量关系式,并说明理由.
(1)、如图①,当点D在线段上时,过点D作 , 且交于点E.求证:;(2)、如图①,在(1)的条件下,求证:;(3)、如图②,当点D在线段的延长线上时,(2)中线段 , , 之间的数量关系式还成立吗?若成立,请加以证明;若不成立,请写出线段 , , 之间新的数量关系式,并说明理由.