陕西省渭南市韩城市2022-2023学年七年级上学期学业水平检测期末数学试题
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
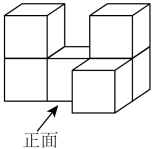
1. 的倒数是( )A、2023 B、 C、 D、2. 如图是由6个小正方体拼成的几何体,该几何体从上面看到的形状图是( )
 A、
A、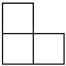 B、
B、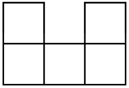 C、
C、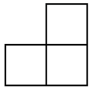 D、
D、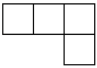 3. 若关于 , 的单项式与的和仍为単项式,则的值为( )A、2 B、5 C、7 D、94. 下面各选项中运用等式的性质进行的变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么5. 把化为用度表示,下列正确的是( )A、 B、 C、 D、6. 已知 , , 则的值为( )A、 B、2 C、14 D、167. 《孙子算经》中有一道题,原文是:今有四人共车,一车空;三人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每4人共乘一车,最终剩余1辆车;若每3人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、8. 一个正方体的展开图如图所示,每一个面上都写有一个自然数并且相对两个面所写的两个数之和相等,那么a+b﹣2c=( )
3. 若关于 , 的单项式与的和仍为単项式,则的值为( )A、2 B、5 C、7 D、94. 下面各选项中运用等式的性质进行的变形正确的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么5. 把化为用度表示,下列正确的是( )A、 B、 C、 D、6. 已知 , , 则的值为( )A、 B、2 C、14 D、167. 《孙子算经》中有一道题,原文是:今有四人共车,一车空;三人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每4人共乘一车,最终剩余1辆车;若每3人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、8. 一个正方体的展开图如图所示,每一个面上都写有一个自然数并且相对两个面所写的两个数之和相等,那么a+b﹣2c=( )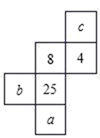 A、40 B、38 C、36 D、34
A、40 B、38 C、36 D、34二、填空题
-
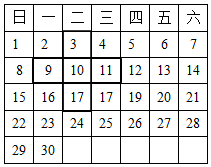
9. 韩城市为了能源结构优化、生态环境保护,以及推动绿色低碳高质量发展,计划投产大唐西庄农光互补光伏发电项目,总投资470000000元.将数据470000000用科学记数法表示为.10. 若与3互为相反数,则等于.11. 若 , 则.(填“>”“<”或“=”)12. 一个角比它的补角少 , 则这个角的余角为.13. 如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如3,9,10,11,17).照此方法,若圈出的5个数中,最大数与最小数的和为38,则这5个数中的最大数为.
三、解答题
-
14. 解方程:.15. 计算:.16. 如图,在平面内有 , , 三点.利用尺规,按下列要求作图:(不写作法,保留作图痕迹)

( 1 )画直线 , 画射线 , 画线段;
( 2 )在线段上任取一点(不同于 , ),连接 , 并延长至点 , 使.
17. 如图是一个计算程序图. (1)、若输入的值为 , 求输出的结果的值;(2)、若输入的值满足 , 输出的结果的值为 , 求输入的值.18. 如图,数轴上从左到右依次有点、、、 , 其中点为原点,、所对应的数分别为、1,、两点间的距离是3.
(1)、若输入的值为 , 求输出的结果的值;(2)、若输入的值满足 , 输出的结果的值为 , 求输入的值.18. 如图,数轴上从左到右依次有点、、、 , 其中点为原点,、所对应的数分别为、1,、两点间的距离是3.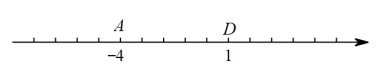 (1)、在图中标出点 , 的位置,并写出点对应的数;(2)、若在数轴上另取一点 , 且、两点间的距离是7,求点所对应的数.19. 已知 , 为有理数,现规定一种新运算“※”,满足.(1)、求的值;(2)、求的值.20. 已知x=3是关于x的方程ax-5=9x-a的解,求关于x的方程a(x-1)-5=9(x-1)-a的解.21. 如图,用同样长的火柴棒按规律搭建图形,图①需要6根火柴棒,图②需要11根火柴棒,图③需要16根火柴棒,……
(1)、在图中标出点 , 的位置,并写出点对应的数;(2)、若在数轴上另取一点 , 且、两点间的距离是7,求点所对应的数.19. 已知 , 为有理数,现规定一种新运算“※”,满足.(1)、求的值;(2)、求的值.20. 已知x=3是关于x的方程ax-5=9x-a的解,求关于x的方程a(x-1)-5=9(x-1)-a的解.21. 如图,用同样长的火柴棒按规律搭建图形,图①需要6根火柴棒,图②需要11根火柴棒,图③需要16根火柴棒,…… (1)、图⑥需要根火柴棒;(2)、按照这个规律,图n需要火柴棒的根数为.(用含a的式子表示)22. 如图,点是线段上一点,并且 , 点 , 分别为 , 的中点.
(1)、图⑥需要根火柴棒;(2)、按照这个规律,图n需要火柴棒的根数为.(用含a的式子表示)22. 如图,点是线段上一点,并且 , 点 , 分别为 , 的中点. (1)、若线段 , 求的值;(2)、若线段 , 求线段的长.(用含的式子表示)23. 科技改变世界.快递分拣机器人从微博火到了朋友圈,据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确放入相应的格口,还会感应避让障碍物、自动归队取包裹,没电的时候还会自己找充电桩充电.某分拣仓库计划平均每天分拣万件包裹,但实际每天的分拣量与计划相比会有出入,下表是该仓库月份第三周分拣包裹的情况(超过计划量的部分记为正,未达到计划量的部分记为负):
(1)、若线段 , 求的值;(2)、若线段 , 求线段的长.(用含的式子表示)23. 科技改变世界.快递分拣机器人从微博火到了朋友圈,据介绍,这些机器人不仅可以自动规划最优路线,将包裹准确放入相应的格口,还会感应避让障碍物、自动归队取包裹,没电的时候还会自己找充电桩充电.某分拣仓库计划平均每天分拣万件包裹,但实际每天的分拣量与计划相比会有出入,下表是该仓库月份第三周分拣包裹的情况(超过计划量的部分记为正,未达到计划量的部分记为负):星期
一
二
三
四
五
六
日
分拣情况(单位:万件)
0
(1)、该仓库本周内分拣包裹数量最多的一天是星期;最少的一天是星期;最多的一天比最少的一天多分拣万件包裹;(2)、该仓库本周实际平均每天分拣多少万件包裹?24. 已知关于的多项式 , , 其中 , ( , 为有理数).(1)、化简;(2)、若的结果不含项和项,求、的值.25. 按照“双减”政策,丰富课后托管服务内容,学校准备订购一批排球和跳绳,经过市场调查后发现排球元/个,跳绳元/根.某体育用品商店提供A、B两种优惠方案(顾客只能选择其中一种方案):A方案:买一个排球送一根跳绳;
B方案:排球和跳绳都按定价的付款.
已知要购买排球个,跳绳根.
(1)、若按A方案购买,一共需付款元;若按B方案购买,一共需付款元;(用含的式子表示)(2)、购买多少根跳绳时,A、B两种方案所需要的钱数一样多?26. 如图,是内部的一条射线,是内部的一条射线,是内部的一条射线.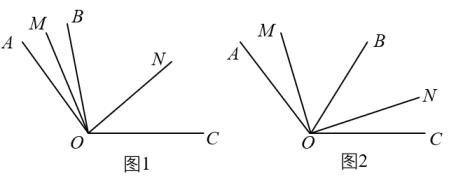 (1)、如图1,、分别是、的角平分线,已知 , , 求的度数;(2)、如图2,若 , , 且 , 求的度数.
(1)、如图1,、分别是、的角平分线,已知 , , 求的度数;(2)、如图2,若 , , 且 , 求的度数.