陕西省宝鸡市凤翔区2022-2023学年七年级上学期期末数学试卷

试卷更新日期：2023-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 2021年10月16日，神舟十三号载人飞船在长征二号F遥十三运载火箭的托举下点火升空，成功对接距地球约386000米的空间站，将数据386000用科学记数法表示（）

A、3.86×10⁶ B、0.386×10⁶ C、3.86×10⁵ D、386×10³

查看试题解析
2. 如图是一个小正方体的表面展开图，把展开图折叠成小正方体后，有“党”字一面的相对面上的字是（）

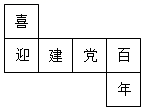A、喜 B、迎 C、百 D、年

查看试题解析
3. 下列调查最适合普查的是（）

A、调查某中学适宜接种新冠疫苗人员的实际接种情况 B、调查国庆期间全国观众最喜爱的电影 C、调查“深圳读书月”活动中市民的读书情况 D、了解一批哈密瓜是否甜

查看试题解析
4. 已知 $x = 4$ 是关于x的方程 $3 x + 2 a = 0$ 的一个解，则a的值是（）

A、 $- 2$ B、 $- 4$ C、 $- 6$ D、 $- 8$

查看试题解析
5. 如图所示， $∠ A O B = 90 °$ ， $∠ B O C = 40 °$ ， OD平分 $∠ A O C$ ，则 $∠ B O D$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $40 °$ D、 $60 °$

查看试题解析
6. 解方程 $\frac{2 x - 1}{2}$ - $\frac{10 x + 1}{4}$ ＝3时，去分母正确的是（）

A、2（2x-1）-10x-1＝3 B、2（2x-1）-10x+1＝3 C、2（2x-1）-10x-1＝12 D、2（2x-1）-10x+1＝12

查看试题解析
7. 把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.若设这个班有x名学生，可列出的方程为（）

A、 $3 x + 20 = 4 x - 25$ B、 $3 (x + 20) = 4 (x - 25)$ C、 $3 x - 25 = 4 x + 20$ D、 $3 x - 20 = 4 x + 25$

查看试题解析
8. 找出以下图形变化的规律，则第 2022 个图形中黑色正方形的数量是（）

A、3030 B、3031 C、3032 D、3033

查看试题解析

二、填空题

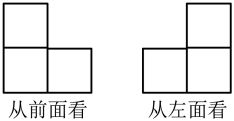
9. 我市某天的最高气温是4℃，最低气温是 $- 1 ℃$ ，则这天的日温差是℃.

查看试题解析
10. 从多边形的一个顶点可以作出6条多边形的对角线，则该多边形的边数是．

查看试题解析
11. $3 x^{m} y^{2}$ 与 $- 2 x^{4} y^{n}$ 是同类项，则 $m^{n}$ 的值是.

查看试题解析
12. 由若干个相同的小正方体搭成的一个几何体从前面和左面看到的形状图如图所示，则组成这个几何体的小正方体的个数最少是.

查看试题解析
13. 如图，已知数轴上的点 $C$ 表示的数为6，点 $A$ 表示的数为 $- 4$ ，点 $B$ 是 $A C$ 的中点，动点 $P$ 从点 $A$ 出发，以每秒2个单位长度的速度沿数轴向右匀速运动，运动时间为 $t$ 秒（ $t > 0$ ），另一动点 $Q$ ，从 $B$ 出发，以每秒1个单位长度的速度沿数轴向左匀速运动，且 $P$ ， $Q$ 同时出发，当 $t$ 为秒时，点 $P$ 与点 $Q$ 之间的距离为2个单位长度.

查看试题解析

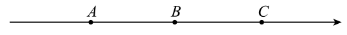
三、解答题

14. 计算： $- 2^{3} - 1 \times {(\frac{1}{2})}^{2} + | 3 - {(- 3)}^{2} |$ .

查看试题解析
15. 解方程： $4 x - 3 (20 - x) = 5 x - 7 (20 - x)$ .

查看试题解析
16. 解方程： $\frac{1 - x}{2} = \frac{4 x - 1}{3} - 1$ .

查看试题解析
17. 已知： $| x - 1 | + {(y + 1)}^{2} = 0$ ，通过化简后求 $2 (x^{2} y + x y) - 3 (x^{2} y - x y) - 4 x^{2} y$ 的值.

查看试题解析
18. 如图，线段AB＝20，BC＝15，点M是AC的中点．

(1)、求线段AM的长度；

(2)、在CB上取一点N，使得CN：NB＝2：3．求MN的长．

查看试题解析
19. 为了落实“双减”政策，发展学生的综合素养，我校积极开展“特色课程”试点活动，根据实际，决定主要开设A：乒乓球，B：网球，C：绘画，D：演讲，四种特长课堂，为了解学生最喜欢哪一种项目，采用抽样调查的方法对部分学生进行调查，并将调查结果绘制成如下统计图，请你结合图中信息解答下列问题.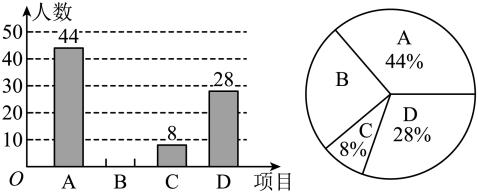

(1)、样本中最喜欢 $B$ 项目的人数百分比是，其所在扇形图中的圆心角的度数是；

(2)、随机抽查了多少学生？请把条形统计图补充完整；

(3)、已知该校有1200人，请统计全校最喜欢乒乓球的人数是多少?

查看试题解析
20. 某治安巡警分队常常在一条东西走向的街道上巡逻一天下午，该巡警分队驾驶电动小汽车从位于这条街道上的某岗亭出发巡逻，如果规定向东为正，向西为负，他们行驶里程（单位： km）如下： $- 6 ， - 2 ， + 8 ， - 3 ， + 6 ， - 4 ， + 6 ， + 3 .$ 问：

(1)、这辆小汽车完成巡逻后位于该岗亭的那一侧？距离岗亭有多少千米？

(2)、已知这种电动小汽车平均每千米耗电 $0.15$ 度，则这天下午小汽车共耗电多少度？

查看试题解析
21. 某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：（注：利润=售价一进价）

甲

乙

进价（元/件）

15

35

售价（元/件）

20

45

若商店计划销售完这批商品后能使利润达到1100元，问甲、乙两种商品应分别购进多少件？

查看试题解析
22. 某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元.“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套，领带 $x$ 条（ $x > 20$ ）.

(1)、若该客户按方案一购买，需付款元.（用含 $x$ 的代数式表示）若该客户按方案二购买，需付款元.（用含 $x$ 的代数式表示）

(2)、若 $x = 40$ ，通过计算说明此时按哪种方案购买较为合算？

(3)、当 $x = 40$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法及费用

查看试题解析
23. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础.
例如：从“形”的角度看： $| 3 - 1 |$ 可以理解为数轴上表示 3 和 1 的两点之间的距离； $| 3 + 1 |$ 可以理解为数轴上表示 3 与-1 的两点之间的距离.
从“数”的角度看：数轴上表示 4 和-3 的两点之间的距离可用代数式表示为： 4-（-3） .

根据以上阅读材料探索下列问题：

(1)、数轴上表示 3 和 9 的两点之间的距离是；数轴上表示 2 和-5 的两点之间的距离是；（直接写出最终结果）

(2)、①若数轴上表示的数 x 和-2 的两点之间的距离是 4，则 x 的值为；
②若 x 为数轴上某动点表示的数，则式子 $| x + 1 | + | x - 3 |$ 的最小值为.

查看试题解析
24. 如图，已知点 $O$ 为直线 $A B$ 上一点，将一直角三角板的直角顶点放在点 $O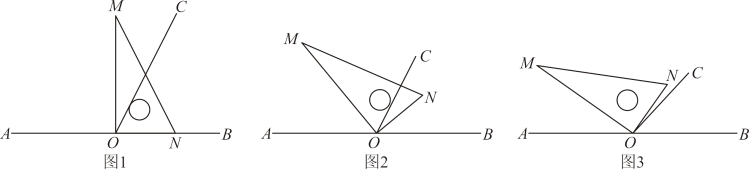$ 处.

(1)、如图1，将三角板的一边 $O N$ 与射线 $O B$ 重合，过点 $O$ 在三角板的内部，作射线 $O C$ ，使 $∠ B O C ： ∠ M O C = 2 ： 1$ ，则 $∠ B O C =$ .

(2)、由（1）中的结论，如图2，将三角板绕点 $O$ 按每秒 $1 0^{∘}$ 的速度沿逆时针方向旋转一周，在旋转的过程中，第 $t$ 秒时， $O N$ 所在的直线恰好平分锐角 $∠ B O C$ ，求此时 $t$ 的值；

(3)、将如图1所示的三角板 $M O N$ 绕点 $O$ 逆时针旋转 $a (0^{∘} < a < 9 0^{∘})$ 到如图3所示的位置，在 $∠ B O N$ 的内部作射线 $O C$ 使得 $∠ N O C = \frac{1}{5} ∠ A O N$ ，则 $∠ B O C$ 的度数为多少?（用含a的代数式表示）

查看试题解析

	甲	乙
进价（元/件）	15	35
售价（元/件）	20	45