陕西省宝鸡市凤翔区2022-2023学年八年级上学期期末数学试卷
试卷更新日期:2023-03-07 类型:期末考试
一、单选题
-
1. 下列四个实数中,无理数是( )A、0 B、 C、 D、2. 下列命题中,是真命题的是( )A、相等的角是对顶角 B、两直线平行,同位角相等 C、对应角相等的两个三角形全等 D、如果|a|=|b|,那么a=b3. 已知是关于、的二元一次方程,则的值为( )A、 B、 C、 D、4. 如图,长方形的边在轴上,与原点重合, , , 点的坐标为.则直线的函数表达式为( )
 A、 B、 C、 D、5. 直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )A、6cm B、8cm C、 cm D、 cm6. 在一次函数中,随的增大而增大,且 , 则在坐标系中它的大致图象是( )A、
A、 B、 C、 D、5. 直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )A、6cm B、8cm C、 cm D、 cm6. 在一次函数中,随的增大而增大,且 , 则在坐标系中它的大致图象是( )A、 B、
B、 C、
C、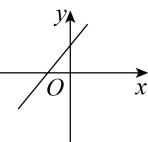 D、
D、 7. 某校八(1)班全体同学喜欢的球类运动如图所示.则从图中可以直接看出( )
7. 某校八(1)班全体同学喜欢的球类运动如图所示.则从图中可以直接看出( ) A、喜欢各种球类的具体人数 B、全班同学一学期来喜欢各种球类的变化情况 C、全班的总人数 D、全班同学现在喜欢各种球类人数的百分比8. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )
A、喜欢各种球类的具体人数 B、全班同学一学期来喜欢各种球类的变化情况 C、全班的总人数 D、全班同学现在喜欢各种球类人数的百分比8. 如图,给出下列条件.①;②;③ , 且;④其中,能推出的条作为( )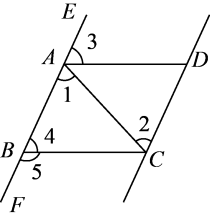 A、①②③ B、①②④ C、①③④ D、②③④9. 已知点 关于x轴的对称点和点 关于y轴的对称点相同,则点 关于x轴对称的点的坐标为( )A、 B、 C、 D、10. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、①②③ B、①②④ C、①③④ D、②③④9. 已知点 关于x轴的对称点和点 关于y轴的对称点相同,则点 关于x轴对称的点的坐标为( )A、 B、 C、 D、10. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
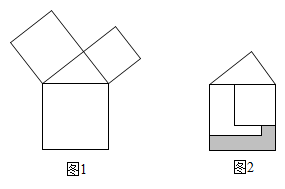 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和二、填空题
-
11. 将直线 向上平移1个单位长度,平移后直线的解析式为 .12. 已知 ,则(a﹣b)2= .13. 若点 , 都在直线上,则a与b的大小关系是 .14. 如图所示,EF⊥AB,∠1=26°,则当AB∥CD时,∠2=°.
 15. 如图,有一个圆柱体,它的高等于 , 半径等于 , 一只蚂蚁在点A处,它要吃到上底面上与A点相对的点B处的食物,沿圆柱体侧面爬行的最短路程是cm(的值取3).
15. 如图,有一个圆柱体,它的高等于 , 半径等于 , 一只蚂蚁在点A处,它要吃到上底面上与A点相对的点B处的食物,沿圆柱体侧面爬行的最短路程是cm(的值取3).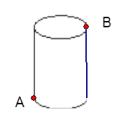
三、解答题
-
16. 计算:17. 解方程组:(1)、;(2)、.18. 已知:如图,∠BAP+∠APD =180°,∠1 =∠2.求证:AE∥PF.
 19. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m)
19. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m) 20. △ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.
20. △ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.
( 1 )作出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;
( 2 )在y轴上作点D,使得AD+BD最小,并求出最小值.
21. 某旅馆的客房有三人间和两人间两种,三人间每人每天25元,两人间每人每天35元,一个50人的旅游团到该旅馆住宿,租住了若干客房,且每个客房正好住满,一天花去住宿费1 510元,两种客房各租住多少间?22. 小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡底跑到坡顶再原路返回坡底.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的倍.设两人出发后距出发点的距离为.图中折线表示小亮在整个训练中与的函数关系,其中点在轴上,点坐标为. (1)、小亮下披的速度是(2)、求出所在直线的函数关系式;23. 为帮助学生了解“预防新型冠状病毒”的有关知识,学校组织了一次线上知识培训,培训结束后进行测试.试题的满分为20分.为了解学生的成绩情况,从七、八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析.下面给出了部分信息:
(1)、小亮下披的速度是(2)、求出所在直线的函数关系式;23. 为帮助学生了解“预防新型冠状病毒”的有关知识,学校组织了一次线上知识培训,培训结束后进行测试.试题的满分为20分.为了解学生的成绩情况,从七、八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析.下面给出了部分信息:抽取的20名七年级学生成绩是:20,20,20,20,19,19,19,19,18,18,18,18,18,18,18,17,16,16,15,14.
抽取的40名学生成绩统计表
性别
七年级
八年级
平均分
18
18
众数
a
b
中位数
18
c
方差
2.7
2.7

根据以上信息,解答下列问题:
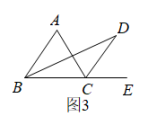
(1)、直接写出表中a,b,c的值:a= , b= , c= .(2)、在这次测试中,你认为是七年级学生成绩好,还是八年级学生成绩好?请说明理由.(3)、若九年级随机抽取20名学生的成绩的方差为2.5,则年级成绩更稳定(填“七”或“八”或“九”).24. 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体的无盖纸盒.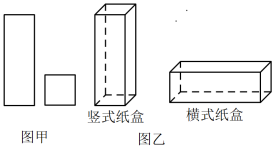 (1)、现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,对可制作横式、竖式两种纸盒各多少个?(2)、若有正方形纸板30张,长方形纸板张,做成上述两种纸盒,纸板恰好用完,其中竖式纸盒做了个,请用含的代数式表示.25. 综合与探究:(1)、【情境引入】如图1,分别是的内角 , 的平分线,说明的理由.
(1)、现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,对可制作横式、竖式两种纸盒各多少个?(2)、若有正方形纸板30张,长方形纸板张,做成上述两种纸盒,纸板恰好用完,其中竖式纸盒做了个,请用含的代数式表示.25. 综合与探究:(1)、【情境引入】如图1,分别是的内角 , 的平分线,说明的理由. (2)、【深入探究】
(2)、【深入探究】①如图2,分别是的两个外角 , 的平分线,与之间的等量关系是 ▲ ;

②如图3,分别是的一个内角和一个外角的平分线,交于点D,探究与之间的等量关系,并说明理由.