陕西省宝鸡市陈仓区2022-2023学年八年级上学期期末考试数学试题

试卷更新日期：2023-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数，是无理数的是（）

A、0 B、 $\frac{23}{7}$ C、 $\sqrt[3]{- 9}$ D、 $\sqrt{16}$

查看试题解析
2. 下列各组数据中是勾股数的是（）

A、0.3，0.4，0.5 B、 $3^{2}$ ， $4^{2}$ ， $5^{2}$ C、9，12，15 D、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$

查看试题解析
3. 2021年6月17日神舟十二号飞船于在甘肃酒泉发射升空，在太空驻留90天后于9月14日返回地球，下列描述能确定飞船着陆位置的是（）

A、内蒙古中部 B、酒泉卫星发射中心东南方向 $1000 k m$ 处 C、东经 $129 ° 2 9^{'} ~ 97 ° 1 0^{'}$ D、北纬 $53 ° 2 0^{'} ~ 37 ° 2 0^{'}$

查看试题解析
4. 如图，已知a∥b，l与a、b相交，若∠1=70°，则∠2的度数等于（）

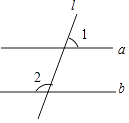A、120° B、110° C、100° D、70°

查看试题解析
5. 已知二元一次方程组 ${\begin{array}{l} x - y = - 5 \\ x + 2 y = - 2 \end{array}$ 的解为 ${\begin{array}{l} x = - 4 \\ y = 1 \end{array}$ ，则在同一平面直角坐标系中，直线 $l_{1}$ ： $y = x + 5$ 与直线 $l_{2}$ ： $y = - \frac{1}{2} x - 1$ 的交点坐标为（）

A、 $(4 ， 1)$ B、 $(1 ， - 4)$ C、 $(- 1 ， - 4)$ D、 $(- 4 ， 1)$

查看试题解析
6. 数据201，202，198，199，200的方差与极差分别是（）

A、1，4 B、2，2 C、2，4 D、4，2

查看试题解析
7. 点 $A (x_{1} ， y_{1})$ 、点 $B (x_{2} ， y_{2})$ 在正比例函数 $y = - 4 x$ 的图像上，当 $x_{1} < x_{2}$ 时，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} = y_{2}$ D、无法判断

查看试题解析
8. 如图，在平面直角坐标系中，直线 $y = 2 x + 4$ 分别与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ 、 $M$ 、 $N$ 分别是 $A B$ 、 $O A$ 的中点，点 $P$ 是 $y$ 轴上的一个动点，当 $P M + P N$ 的值最小时，点 $P$ 的坐标为（）

A、 $(0 ， 2)$ B、 $(0 ， \frac{3}{2})$ C、 $(0 ， 1)$ D、 $(0 ， \frac{1}{2})$

查看试题解析

二、填空题

9. 比较大小： $2 \sqrt{6}$ $3 \sqrt{3}$ .（填“＞”“＜”或“＝”）

查看试题解析
10. 如图，已知A村庄的坐标为 $(2 ， - 3)$ ，一辆汽车从原点O出发在x轴上行驶.行驶过程中汽车离A村最近的距离为.

查看试题解析
11. 小明某学期的数学平时成绩80分，期中考试90分，期末考试88分，若计算学期总评成绩的方法如下：平时：期中：期末=2：3：5，则小明学期总评成绩是分.

查看试题解析
12. 如图，若∠1与∠2互补，∠3与∠2互补，则 $∠ 1 = ∠ 3$ ，用一个定理表达你所得到的结论.

查看试题解析
13. 如图，四边形 $A B C D$ 中， $A C ⊥ B D$ 于 $O$ ， $A B = 6$ ， $B C = 8$ ， $C D = 10$ ，则 $A D$ 的长为 .

查看试题解析

三、解答题

14. 化简：

(1)、 $\sqrt{72} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12}$

(2)、 $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$

查看试题解析
15. 解下列方程组：

(1)、 ${\begin{array}{l} y = 3 x \\ 7 x - 2 y = 2 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{2} - \frac{y + 1}{3} = 1 \\ 3 x + 2 y = 40 \end{array}$

查看试题解析
16. 如图，在正方形网格中，每个小正方形的边长为1，格点 $△ A B C$ 的顶点A，B的坐标分别为 $(- 2 ， 1)$ ， $(0 ， 3)$ .

（ 1 ）请在图中建立适当的直角坐标系.

（ 2 ）画出 $△ A B C$ 关于x轴对称的 $△ A^{'} B^{'} C^{'}$ ，并直接写出点 $C^{'}$ 的坐标.

查看试题解析
17. 尺规作图，如图过点A作直线l的平行线 $A B$ （不写作法，保留作图痕迹）.

查看试题解析
18. 如图，在平面直角坐标系中，四边形 $O A B C$ 各顶点的坐标分别是 $O (0 ， 0)$ ， $A (0 ， 12)$ ， $B (- 10 ， 8)$ ， $C (- 14 ， 0)$ ，求四边形 $O A B C$ 的面积.

查看试题解析
19. 如图，AB∥DG，∠1+∠2＝180°，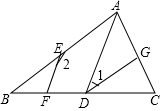

(1)、求证：AD∥EF；

(2)、若DG是∠ADC的平分线，∠2＝150°，求∠B的度数．

查看试题解析
20. “99公益日”是一年一度的全民公益活动日，学校组织学生参加慈善捐款活动，为了解学生捐款情况，随机调查了该校的部分学生，根据调查结果，绘制了如下的统计图1和图2．请根据相关信息，解答下列问题：

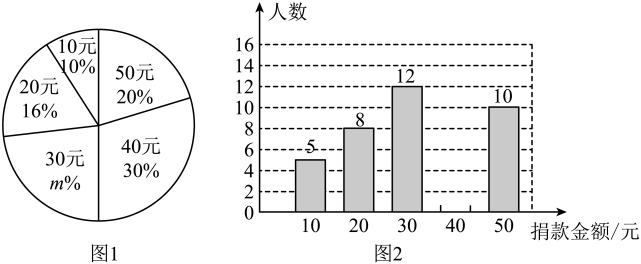(1)、本次接受调查的学生人数为，图1中m的值为．

(2)、求统计的这组学生的捐款数据的平均数、众数和中位数．

(3)、根据统计的这组学生所捐款的情况，若该校共有1000名学生，估计该校共筹得善款多少元？

查看试题解析
21. 如图，在△ABC中，AB=4，BC= $\sqrt{5}$ ，点D在AB上，且BD=1，CD=2．

(1)、求证：CD⊥AB；

(2)、求AC的长．

查看试题解析
22.

(1)、先填表（图①），再根据图①在图②坐标系中画出一次函数 $y = - 2 x + 4$ 的图象；
x
0
$y = - 2 x + 4$
0

(2)、画出把一次函数 $y = - 2 x + 4$ 的图象向左平移3个单位长度后的函数图象，请求平移后的函数的表达式.

查看试题解析
23. 垃圾对环境的影响日益严重，垃圾危机的警钟被再次拉响.我市某中学积极响应国家号召，落实垃圾“分类回收，科学处理”的政策，准备购买 $A$ 、 $B$ 两种型号的垃圾分类回收箱共20只，放在校园各个合适位置，以方便师生进行垃圾分类投放.若购买 $A$ 型14只、 $B$ 型6只，共需4240元；若购买 $A$ 型8只、 $B$ 型12只，共需4480元.求 $A$ 型、 $B$ 型垃圾分类回收箱的单价.

查看试题解析
24. 如图，欣欣妈妈在超市购买某种水果所付金额 $y$ （元）与购买 $x$ （千克）之间的函数图象如图所示，

(1)、求 $x \geq 4$ 时， $y$ 与 $x$ 之间的函数关系；

(2)、请你帮欣欣妈妈计算：一次性购买 $6$ 千克这种水果比平均分 $2$ 次购买可节省多少元？

查看试题解析
25. 问题情境
在综合与实践课上，同学们以“一个含 $30 °$ 的直角三角尺和两条平行线”为背景开展数学活动如图1，已知两直线a，b且 $a ∥ b$ 和直角三角形 $A B C$ ， $∠ B C A = 90 °$ ， $∠ B A C = 30 °$ ， $∠ A B C = 60 °$ .

(1)、在图1中， $∠ 1 = 46 °$ ，求 $∠ 2$ 的度数；

(2)、如图2，创新小组的同学把直线a向上平移，并把 $∠ 2$ 的位置改变，发现 $∠ 2 - ∠ 1$ 是一个定值，请写出这个定值，并说明理由；

(3)、缜密小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3， $A C$ 平分 $∠ B A M$ ，此时发现 $∠ 1$ 与 $∠ 2$ 又存在新的数量关系，请直接写出 $∠ 1$ 与 $∠ 2$ 的数量关系.

查看试题解析