江苏省淮安市淮安经济技术开发区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，是随机事件的是（）

A、太阳每天早晨从西边升起 B、 $△ A B C$ 中， $A B + A C > B C$ C、两个负数相乘，积为正 D、两个数相加，和大于其中的一个加数

查看试题解析
3. 下列调查中，适合采用全面调查方式的是（）

A、对大运河水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班 $40$ 名同学体重情况的调查 D、对江苏省中小学的视力情况的调查

查看试题解析
4. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（　　）

A、 $\sqrt{18}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{24}$ D、 $\sqrt{0.3}$

查看试题解析
5. 下列计算中，正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $(2 \sqrt{3})^{2} = 12$ D、 $\sqrt{8} \div \sqrt{4} = 2$

查看试题解析
6. 分式 $\frac{- x}{x^{2} - x y}$ 可化简为（）

A、 $- \frac{1}{x - y}$ B、 $- \frac{1}{x + y}$ C、 $\frac{1}{x + y}$ D、 $\frac{1}{x - y}$

查看试题解析
7. 已知反比例函数 $y = \frac{2}{x}$ ，下列结论中，不正确的是（）

A、图象必经过点（1，2） B、y随x的增大而增大 C、图象在第一、三象限内 D、若x＞1，则0＜y＜2

查看试题解析
8. 已知平行四边形ABCD中，对角线AC、BD相交于O.则下列说法准确的是（）

A、当 $OA = OC$ 时，平行四边形ABCD为矩形 B、当 $AB = AD$ 时，平行四边形ABCD为正方形 C、当 $∠ ABC = 90^{°}$ 时，平行四边形ABCD为菱形 D、当 $AC ⊥ BD$ 时，平行四边形ABCD为菱形

查看试题解析

二、填空题

9. 若分式 $\frac{2}{x - 5}$ 有意义，则x的取值范围是.

查看试题解析
10. 在一个不透明的袋子里装有若干个白球和15个黄球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄球的频率稳定在0.75，则袋中白球有个.

查看试题解析
11. 若反比例函数 $y = \frac{m + 1}{x}$ 的图象在二、四象限，则m的取值范围为.

查看试题解析
12. 将分式 $- \frac{8 a^{6} b}{12 a^{2} b^{2}}$ 约分结果是.

查看试题解析
13. 已知▱ABCD的周长是20cm，且AB：BC=3：2，则AB=cm.

查看试题解析
14. 已知点A₁(-1，y₁)，A₂(-3，y₂)都在反比例函数y= $\frac{k}{x}$ (k>0)的图像上，则y₁与y₂的大小关系为.

查看试题解析
15. 如图， $R t △ A B C$ 的一个顶点B在原点，BC在y轴上，直角边 $A C = 1$ ， $B C = 2$ ，把 $R t △ A B C$ 绕点B逆时针旋转90°，顶点A的对应点为 $A^{'}$ .若反比例函数 $y = \frac{m}{x}$ 的图象经过点 $A^{'}$ ，则m的值为.

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $A D = 2$ ， $E$ 为边 $C D$ 的中点，点 $P$ 在线段 $A B$ 上运动， $F$ 是 $C P$ 的中点，则 $Δ C E F$ 的周长的最小值是.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{3} + \sqrt{2} \times \sqrt{6}$ ；

(2)、 $1 + \frac{x + 2}{x - 1} \div \frac{x + 2}{x + 1}$

查看试题解析
18. 解方程： $\frac{3}{x} = \frac{2}{x - 2}$

查看试题解析
19. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div \frac{a + 1}{a - 1}$ ，其中 $a = \sqrt{2} + 1$ .

查看试题解析

20. 某初中学校对本校初中学生完成家庭作业的时间做了总量控制，规定每天完成家庭作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查，并绘制出频数分布表和频数分布直方图的一部分.

时间（小时）	频数（人数）	频率
0≤t＜0.5	4	0.1
0.5≤t＜1	a	0.3
1≤t＜1.5	10	0.25
1.5≤t＜2	8	b
2≤t＜2.5	6	0.15
合计		1

(1)、a= ， b=；

(2)、补全频数分布直方图；

(3)、请估计该校800名初中学生中，约有多少学生在1.5小时以内完成家庭作业.

查看试题解析

21. 甲、乙两个机器人检测零件，甲比乙每小时多检测10个，甲检测300个与乙检测200个所用的时间相等.甲、乙两个机器人每小时各检测零件多少个？

查看试题解析
22. 如图，在平行四边形ABCD中，E为BC的中点，连接DE.延长DE交AB的延长线于点F.求证：AB=BF.

查看试题解析
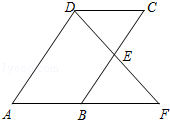23. 正比例函数 $y_{1} = 2 x$ 的图象与反比例函数 $y_{2} = \frac{k}{x}$ 的图象有一个交点P的横坐标是2.

(1)、求k的值和两个函数图象的另一个交点坐标；

(2)、直接写出 $y_{1} > y_{2} > 0$ 的解集为.

(3)、根据图象，直接写出当 $- 4 < x < - 1$ 时， $y_{2}$ 的取值范围为.

查看试题解析
24. 如图，平面直角坐标系中点D坐标为（1，1），每个小正方形网格的顶点叫做格点，平行四边形ABCD的顶点均在格点上．仅用无刻度直尺在给定网格中按要求作图，作图过程用虚线表示，作图结果用实线表示．

（ 1 ）将线段AD绕点A逆时针旋转90°，画出对应线段AE，并直接写出点E的坐标；

（ 2 ）过（1）中点E画一条直线把平行四边形ABCD分成面积相等的两部分；
（ 3 ）找一个格点F，使得CF⊥AD，并直接写出点F的坐标．

查看试题解析
25. 阅读下面问题：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$
$\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$
…

(1)、 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ （n为正整数）.

(2)、 $\frac{1}{3 \sqrt{2} + \sqrt{17}} =$ .

(3)、求 $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{2 + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2022} + \sqrt{2021}}) (\sqrt{2022} + 1)$ 的值.

查看试题解析
26. 如图，菱形OABC的点B在y轴上，点C坐标为（4，3），双曲线 $y = \frac{k}{x}$ 的图象经过点A.

(1)、菱形OABC的边长为；

(2)、求双曲线的函数关系式；

(3)、①点B关于点O的对称点为D点，过D作直线l垂直于y轴，点P是直线l上一个动点，点E在双曲线上，当P、E、A、B四点构成平行四边形时，求点E的坐标；
②将点P绕点A逆时针旋转90°得点Q，当点Q落在双曲线上时，求点Q的坐标.

查看试题解析