湖南省益阳市六校2022-2023学年七年级上学期期末联考数学试题

试卷更新日期：2023-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为44亿人，这个数用科学记数法表示为（）

A、 $44 \times 1 0^{8}$ B、 $4.4 \times 1 0^{9}$ C、 $4.4 \times 1 0^{8}$ D、 $4.4 \times 1 0^{10}$

查看试题解析
2. $- 2$ 的相反数是（）

A、 $- \frac{1}{2}$ B、 $- 2$ C、 $\frac{1}{2}$ D、2

查看试题解析
3. 按如图所示的运算程序，能使输出 $y$ 值为 $5$ 的是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 2$ ， $n = 0$ C、 $m = 2$ ， $n = 2$ D、 $m = 3$ ， $n = 2$

查看试题解析
4. 如图，数轴上A、B两点对应的实数分别为a，b，则下列结论不正确的是（）

A、a+b＞0 B、ab＜0 C、a-b＜0 D、|a|-|b|＞0

查看试题解析
5. 下列代数式中多项式的个数有（）
$2 a$ ； $\frac{m - n}{6}$ ； $\frac{3}{π} + a$ ； $\frac{5}{a - b}$ ； $2 (x^{2} - 4)$ .

A、2 B、3 C、4 D、5

查看试题解析
6. 某工厂第二季度的产值比第一季度的产值增长了x%，第三季度的产值又比第二季度的产值增长了x%，则第三季度的产值比第一季度的产值增长了（）

A、2x% B、1+2x% C、（1+x%）x% D、（2+x%）x%

查看试题解析
7. 已知（k-1）x^|k|+3=0是关于x的一元一次方程.则此方程的解是（）

A、 $- 1$ B、 $- \frac{3}{2}$ C、 $\frac{3}{2}$ D、 $\pm 1$

查看试题解析
8. 两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的 $\frac{1}{3}$ ，这时增加了乙队，两队又共同工作了半个月，总工程全部完成，如果乙队单独完成总工程需多少个月？设乙队单独完成总工程共需 $x$ 个月，则下列方程正确的是（）

A、 $\frac{1}{3} + \frac{1}{2} + \frac{1}{x} = 1$ B、 $\frac{1}{3} + \frac{1}{6} + \frac{1}{x} = 1$ C、 $\frac{1}{3} + \frac{1}{2} + \frac{1}{2 x} = 1$ D、 $\frac{1}{3} + \frac{1}{2} (\frac{1}{3} + \frac{1}{x}) = 1$

查看试题解析
9. 下列几何体中，是圆锥的为（）

A、 B、 C、 D、

查看试题解析
10. 点C是线段AB的中点，点D是线段AC的三等分点．若线段 $A B = 12 c m$ ，则线段BD的长为（）

A、10cm B、8cm C、8cm或10cm D、2cm或4cm

查看试题解析
11. 如图，在同一平面内， $∠ A O B = ∠ C O D = 90 °$ ， $∠ C O E = ∠ B O E$ ，点 $F$ 为 $O E$ 反向延长线上一点（图中所有角均指小于 $180 °$ 的角）.下列结论：① $∠ A O E = ∠ D O E$ ；② $∠ A O D + ∠ C O B = 180 °$ ；③ $∠ C O B － ∠ A O D = 90 °$ ；④ $∠ C O E + ∠ B O F = 180 °$ .其中正确结论的个数有（）.

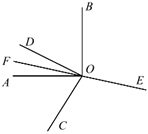A、4个 B、3个 C、2个 D、1个

查看试题解析
12. 如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点 $M_{1} ， N_{1}$ ；第二次操作：分别取线段 $A M_{1}$ 和 $A N_{1}$ 的中点 $M_{2} ， N_{2}$ ；第三次操作：分别取线段 $A M_{2}$ 和 $A N_{2}$ 的中点 $M_{3} ， N_{3}$ ；……连续这样操作10次，则每次的两个中点所形成的所有线段之和 $M_{1} N_{1} + M_{2} N_{2} + ⋯ + M_{10} N_{10} =$ （）

A、 $20 - \frac{10}{2^{9}}$ B、 $20 + \frac{10}{2^{9}}$ C、 $20 - \frac{10}{2^{10}}$ D、 $20 + \frac{10}{2^{10}}$

查看试题解析

二、填空题

13. 比较大小： $- {(\frac{1}{3})}^{2}$ $- {(\frac{1}{2})}^{3}$ （填 $>$ 或者 $<$ 或者 $=$ ）.

查看试题解析
14. 若 $| x + 1 | + {(y - 2)}^{2} = 0$ ，则 $x - y =$ .

查看试题解析
15. 现定义新运算“ $\otimes$ ”，对任意有理数 $a ， b$ ，规定 $a \otimes b = a b + a - b$ ，例如： $1 \otimes 2 = 1 \times 2 + 1 - 2 = 1$ ，则计算 $3 \otimes (- 5) =$ .

查看试题解析
16.
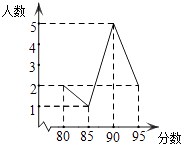
在义乌市中小学生“人人会乐器”演奏比赛中，某班10名学生成绩统计如图所示，则这10名学生成绩的中位数是分，众数是分．

查看试题解析
17. 如图，已知线段 $A B = 12 c m$ ，点 $C$ 是线段 $A B$ 上的任意一点，点 $D ， E$ 分别是线段 $A C$ 和 $B C$ 的中点，则线段 $D E =$ $c m$ .

查看试题解析
18. 对于任意四个有理数 $a ， b ， c ， d$ 可以组成两个有理数对 $(a ， b)$ 与 $(c ， d)$ .我们规定： $(a ， b) ★ (c ， d) = b c - a d$ .例如： $(1 ， 2) ★ (3 ， 4) = 2 \times 3 - 1 \times 4 = 6 - 4 = 2$ .当满足等式 $(- 7 ， 2 x - 1) ★ (- 2 ， x) = 29$ 时， $x$ 的值为.

查看试题解析

三、解答题

19. 计算：

(1)、 $- 2.4 + 3.5 - 4.6 + 4.5 ．$

(2)、 $- 3^{2} + 8 ．$

(3)、 $5 \times (- 2) + 6 \div (- 3)$ .

(4)、 $(- 12) \times (\frac{1}{6} - \frac{1}{4} + \frac{1}{12})$ .

查看试题解析
20. 已知 $A = 3 a^{2} - 4 a b$ ， $B = a^{2} + 2 a b$ .

(1)、求 $A - 2 B$ ；

(2)、若 $| a + 1 | + {(2 - b)}^{2} = 0$ ，求 $A - 2 B$ 的值.

查看试题解析
21. 今年植树节，东方红中学组织师生开展植树造林活动，为了了解全校 $800$ 名学生的植树情况，随机抽样调查 $50$ 名学生的植树情况，制成如下统计表和条形统计图（均不完整）.
植树数量（棵）
频数（人）
频率
3
5
$0.1$
4
$20$
$0.4$
5
6
$10$
$0.2$
合计
$50$
1

(1)、将统计表和条形统计图补充完整；

(2)、求抽样的 $50$ 名学生植树数量的平均数；

(3)、根据抽样数据，估计该校 $800$ 名学生的植树数量.

查看试题解析
22. 山西临猗县临晋镇西关小学校长张鹏飞领着全校 $700$ 多名孩子跳鬼步舞，动作非常魔性.在网络走红后，学校纷纷效仿，某商场看准商机，需订购一批跳鬼步舞的舞蹈鞋，现有甲、乙两个供货商，均标价每双 $100$ 元.为了促销，甲说：“凡来我处进货一律八折.“乙说：“凡来我处进货，如果超出 $80$ 双，则超出的部分打七折”.

(1)、该商场购买多少双舞蹈鞋时，去甲、乙两个供货商处的进货价钱一样多？

(2)、若该商场要订购 $300$ 双舞蹈鞋，应该选哪个供货商更省钱？为什么？

查看试题解析
23. 如图，OC在∠BOD内.

(1)、如果∠AOC和∠BOD都是直角.
①若∠BOC=60°，则∠AOD的度数是 ▲ ；
②猜想∠BOC与∠AOD的数量关系，并说明理由；

(2)、如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数.

查看试题解析
24. 已知：b是最小的正整数，且a、b、c满足（c﹣5）²+|a+b|＝0，请回答问题：

(1)、请直接写出a、b、c的值．a＝，b＝，c＝

(2)、a、b、c所对应的点分别为A、B、C，点P为一动点，其对应的数为x，点P在0到2之间运动时（即0≤x≤2时），请化简式子：|x+1|﹣|x﹣1|+2|x+5|（请写出化简过程）

(3)、在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC﹣AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值

查看试题解析

植树数量（棵）	频数（人）	频率
3	5	$0.1$
4	$20$	$0.4$
5
6	$10$	$0.2$
合计	$50$	1