2022-2023学年第二学期高一物理人教版（2019）必修二 7.3 万有引力定律的成就 过关检测
试卷更新日期：2023-03-07 类型：同步测试
一、单选题
-
1. 若某星球的质量和半径均为地球的一半，那么质量为50kg的宇航员在该星球上的重力是地球上重力的（ ）A、1/4 B、1/2 C、2倍 D、4倍2. 已知引力常数G与下列哪些数据，不可以计算出地球质量（ ）A、地球绕太阳运动的周期及地球离太阳的距离 B、月球绕地球运行的周期及月球绕地球转的轨道半径 C、人造地球卫星在地面附近绕行的速度和运行周期 D、若不考虑地球自转，已知地球半径和地表的重力加速度3. 绳系卫星是由一根绳索栓在一个航天器上的卫星，可以在这个航天器的下方或上方一起绕地球运行 如图所示，绳系卫星a系在航天飞机b上方，当它们一起在赤道上空共同绕地球作匀速圆周运动时 绳长不可忽略 下列说法正确的是（ ）
A、绳系卫星的线速度比航天飞机的线速度大 B、绳系卫星的角速度比航天飞机的角速度小 C、绳系卫星的周期比航天飞机的周期大 D、绳系卫星的向心加速度比航天飞机的向心加速度小4. 人造地球卫星绕地球做匀速圆周运动，假如卫星的线速度减小到原来的 ，卫星仍然做匀速圆周运动，则（ ）A、 卫星的向心加速度减小到原来的 B、卫星的周期增大到原来的8倍 C、 卫星的角速度减小到原来的 D、卫星的周期增大到原来的2倍5. 一颗小行星绕太阳做匀速圆周运动的轨道半径是地球公转半径的4倍，则这颗小行星的运行速率是地球运行速率的( )A、4倍 B、2倍 C、0.5倍 D、16倍6. 黑洞是一种密度极大、引力极大的天体，以至于光都无法逃逸，即黑洞的第二宇宙速度大于光速(光速为c)。某研究人员发现了一个异常小的黑洞，其质量只有太阳的4倍。已知太阳的质量为ms ， 太阳半径为Rs ， 引力常量为G，第二宇宙速度是第一宇宙速度的倍。则该黑洞的半径最大是（ ）A、 B、 C、 D、二、多选题
-
7. 为了测量某行星的质量和半径，宇航员记录了登陆舱在该行星表面做圆周运动的周期T，登陆舱在行星表面着陆后，用弹簧称称量一个质量为m的砝码读数为N．已知引力常量为G．则下列计算中错误的是A、该行星的质量为 B、该行星的半径为 C、该行星的密度为 D、在该行星的第一宇宙速度为8. 如图所示，飞行器P绕某星球做匀速圆周运动，星球相对飞行器的张角为θ ， 万有引力常量为G ， 下列说法正确的是( ）
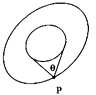A、轨道半径越大，周期越长 B、轨道半径越大，速度越大 C、若测得周期和张角，可得到星球的平均密度 D、若测得周期和轨道半径，可得到星球的平均密度9. 一卫星绕地球做匀速圆周运动，其轨道半径为r，卫星绕地球做匀速圆周运动的周期为T，已知地球的半径为R，地球表面的重力加速度为g，引力常量为G，则地球的质量可表示为（ ）A、 B、 C、 D、10.经长期观测，人们在宇宙中已经发现了“双星系统”．“双星系统”由相距较近的恒星组成，每个恒星的半径远小于两个恒星之间的距离，而且双星系统一般远离其他天体，它们在相互间的万有引力作用下，绕某一点做匀速圆周运动，如图所示为某一双星系统，A星球的质量为m1 ， B星球的质量为m2 ， 它们中心之间的距离为L，引力常量为G，则下列说法正确的是（ ）
A、A星球的轨道半径为R= L B、B星球的轨道半径为r= L C、双星运行的周期为T=2πL D、若近似认为B星球绕A星球中心做圆周运动，则B星球的运行周期为T=2πL三、计算题
-
11. 卡文迪许把他自己的实验说成是“称地球的重量”（严格地说应是“测量地球的质量”）．如果已知引力常量G、地球半径R和地球表面重力加速度g ， 计算地球的质量M和地球的平均密度各是多少？
四、综合题
-
12. 宇航员发现一未知天体，欲将星球的质量、密度等信息传回地面，宇航员只有一块秒表和一个弹簧测力计，他站在星球上随星球转了一圈测得时间为 ，又用弹簧秤测同一质量为m的物体的重力，在“两极”为F，在“赤道”上的读数是其“两极”处的90%，万有引力常量为G，求：(1)、该星球的密度和质量；(2)、当宇航员在该星球“赤道”上时，有一颗绕该星球表面附近匀速转动的行星，其转动周期为T，已知T< ，若此时刚好在他的正上方，则过多久该行星再次出现在他的正上方?
-