2023年江苏省南京市中考数学风向标模拟试题一
试卷更新日期:2023-03-07 类型:中考模拟
一、单选题(每题2分,共12分)
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
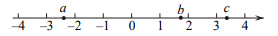 A、 B、 C、 D、3. 如图,在数轴上 , , , 四个点中,点 最可能表示的实数是( ).
A、 B、 C、 D、3. 如图,在数轴上 , , , 四个点中,点 最可能表示的实数是( ). A、 B、 C、 D、4. 如图,是的内接三角形, , 的半径为 , 若点P是上的一点, , 则的长为( )
A、 B、 C、 D、4. 如图,是的内接三角形, , 的半径为 , 若点P是上的一点, , 则的长为( ) A、 B、 C、 D、5. 如图,点D,E分别在△ABC的边AB,AC上,且AD = 1,BD = 5,AE = 2,∠AED = ∠B,则AC的长是( )
A、 B、 C、 D、5. 如图,点D,E分别在△ABC的边AB,AC上,且AD = 1,BD = 5,AE = 2,∠AED = ∠B,则AC的长是( ) A、2.4 B、2.5 C、3 D、4.56. 如图,已知正方形 的边长为2,点 是正方形内部一点,连接 , 满足 ,点 是 边上一动点,连结 , .则 长度的最小值为( )
A、2.4 B、2.5 C、3 D、4.56. 如图,已知正方形 的边长为2,点 是正方形内部一点,连接 , 满足 ,点 是 边上一动点,连结 , .则 长度的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题2分,共20分)
-
7. 当x满足时, 在实数范围内有意义.8. “学中共党史,庆建党百年”,截至4月26日,某市党员群众参与答题次数达8420000次,掀起了党史学习竞赛的热潮,数据“8420000”用科学记数法可表示为 .9. 分解因式: ;分式方程: 解为 .10. 设 , 是方程 的两根,则 的值为 .
11. 计算: =。12. 为了解我市城区居民日常出行方式的情况.某学习小组进行了问卷调查,共收回600份调查问卷,结果统计如下:出行方式
坐公交车
骑自行车、电动车
开私家车
坐单位班车
人数
280
240
65
15
根据以上调查结果,在制作扇形统计图时,以“骑自行车、电动车”为出行方式所在扇形的圆心角的度数为 .
13. Rt△ABC中,∠C=90°,AC=6,BC=8,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是 .14. 如图,矩形 的顶点 分别在 轴、 轴的正半轴上, 为 的中点,反比例函数 的图象经过点 ,且与 交于点 ,连接 , , ,若 的面积为3,则 的值为. 15. 在△ABC中,点D为AC边的中点,于点E,△DEF为等边三角形,若 , , 则DE的长为 .
15. 在△ABC中,点D为AC边的中点,于点E,△DEF为等边三角形,若 , , 则DE的长为 .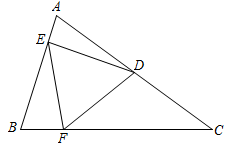 16. “一切为了U”是常山在赶考共同富裕道路上,最新确定的城市品牌.已知线段 , 对于坐标平面内的一个动点P,如果满足 , 则称点P为线段的“U点”,如图,二次函数与x轴交于点A和点B.(1)线段的长度为;(2)若线段的“U”点落在y轴的正半轴上,则该“U点”的坐标为 .
16. “一切为了U”是常山在赶考共同富裕道路上,最新确定的城市品牌.已知线段 , 对于坐标平面内的一个动点P,如果满足 , 则称点P为线段的“U点”,如图,二次函数与x轴交于点A和点B.(1)线段的长度为;(2)若线段的“U”点落在y轴的正半轴上,则该“U点”的坐标为 .
三、解答题(共11题,共88分)
-
17. 解不等式组 , 并写出它的所有整数解.18. 化简求值: ,其中 ;19. 课堂上,同学们在讨论解答数学课本50页综合运用的第9题“如图,在梯形ABCD中,AB∥CD,已知∠A=∠B,求证AD=BC.”时,提出了两种解答思路:
思路1:过一个顶点作另一条腰的平行线,将梯形转化为等腰三角形和平行四边形;
思路2:过同一底上的两个顶点作另一底的垂线段,将梯形转化为直角三角形和矩形;请结合以上思路,选用一种方法证明上题.
 20. 在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到的球是红球的概率为 .(1)、求袋中黄球的个数;(2)、第一次任意摸出一个球(不放回),第二次再摸出一个球,利用树状图或刘表格求两次摸到球的颜色是红色与黄色的概率.21. 2021年,我国粮食总产量再创新高.小刘同学登录国家统计局网站,查询到了我国2021年31个省、直辖市、自治区的粮食产量数据(万吨).并对数据进行整理、描述和分析.下面给出了部分信息.
20. 在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,蓝球1个,若从中任意摸出一个球,摸到的球是红球的概率为 .(1)、求袋中黄球的个数;(2)、第一次任意摸出一个球(不放回),第二次再摸出一个球,利用树状图或刘表格求两次摸到球的颜色是红色与黄色的概率.21. 2021年,我国粮食总产量再创新高.小刘同学登录国家统计局网站,查询到了我国2021年31个省、直辖市、自治区的粮食产量数据(万吨).并对数据进行整理、描述和分析.下面给出了部分信息.a.反映2021年我国31个省、直辖市、自治区的粮食产量数据频数分布直方图如图(数据分成8组: , , , , , , , ):

b.2021年我国各省、直辖市、自治区的粮食产量在这一组的是:
10928,1094.9,1231.5,1270.4,1279.9,1386.5,1421.2,1735.8,1930.3(1)、2021年我国各省、直辖市、自治区粮食产量的中位数为万吨;(2)、小刘同学继续收集数据的过程中,发现北京市与河南省的单位面积粮食产量(千克/公顷)比较接近,如下图所示,他将自2016年至2021年北京市与河南省的单位面积粮食产量表示出来:()

自2016-2021年间,设北京市单位面积粮食产量的平均值为 , 方差为;河南省单位面积粮食产量的平均值为 , 方差为;则 , (填写“”或“<”);
(3)、国家统计局公布,2021年全国粮食总产量13657亿斤,比上一年增长2.0%.如果继续保持这个增长率,计算2022年全国粮食总产量约为多少亿斤(保留整数).22. 亲爱的同学,你能利用一张矩形纸片折出大小不一的菱形吗?请你动手试一试!然后按要求完成下面问题: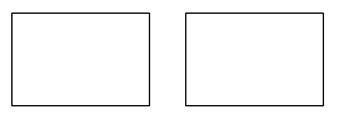
已知某矩形长为8,宽为6,请你用虚线在下图中分别画出两种不同折法的菱形的示意图
并在下方横线上直接写出菱形的面积(画图特别说明: ①示意图中体现所有折痕;②菱形的顶点必须都在矩形的边上 ;③所画菱形是能仅用已知数据便可求出面积的图形)
23. A、B两地相距19.2km,甲、乙两人相向而行,两人的运动速度保持不变。甲从A地向B地出发,当甲运动一段时间后,乙从B地向A地出发,甲、乙两人同时运动时他们之间的距离y(km)与乙运动时间t(h)满足一次函数关系式,其图象如图所示. (1)、根据图像求y与t的函数关系式,并求出两人的速度和;(2)、已知甲由A地运动到B地所用时间是乙由B地运动到A地所用时间的倍.求甲由A地运动到B地所用时间是多少小时?24. 如图1是某小区门口的门禁自动识别系统,主要由可旋转高清摄像机和其下方固定的显示屏.图2是其结构示意图,摄像机长 , 点为摄像机旋转轴心,为的中点,显示屏的上沿与平行, , 与连接杆 , , , 点到地面的距离为 . 若与水平地面所成的角的度数为 .
(1)、根据图像求y与t的函数关系式,并求出两人的速度和;(2)、已知甲由A地运动到B地所用时间是乙由B地运动到A地所用时间的倍.求甲由A地运动到B地所用时间是多少小时?24. 如图1是某小区门口的门禁自动识别系统,主要由可旋转高清摄像机和其下方固定的显示屏.图2是其结构示意图,摄像机长 , 点为摄像机旋转轴心,为的中点,显示屏的上沿与平行, , 与连接杆 , , , 点到地面的距离为 . 若与水平地面所成的角的度数为 .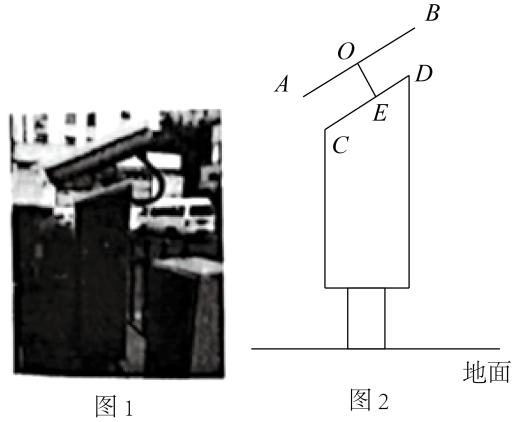 (1)、求显示屏所在部分的宽度;(2)、求镜头到地面的距离.(参考数据: , , , 结果保留一位小数)25. 如图,钝角中, , 为的外接圆,点为优弧上一点(不与 , 重合),连接 , , 交于点 , 的内心恰好落在上.
(1)、求显示屏所在部分的宽度;(2)、求镜头到地面的距离.(参考数据: , , , 结果保留一位小数)25. 如图,钝角中, , 为的外接圆,点为优弧上一点(不与 , 重合),连接 , , 交于点 , 的内心恰好落在上. (1)、求证:AB∥CD;(2)、连接 , 求证:;(3)、若 , , 求的长.26. 把函数的图像绕点旋转180°,得到新函数C2的图像,我们称是关于点P的相关函数.C2的图像的对称轴与x轴交点坐标为(t,0).(1)、填空:t的值为(用含m的代数式表示).(2)、若 , 当时,函数C1的最大值为y1 , 最小值为y2 , 且 , 求C2的解析式.(3)、当时,C2的图像与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段原点O逆时针旋转90°,得到它的对应线段 , 若线与C2的图像有公共点,结合函数图象,求a的取值范围.27. 问题背景:如图1,在 中, , , ,四边形 是正方形,求图中阴影部分的面积.
(1)、求证:AB∥CD;(2)、连接 , 求证:;(3)、若 , , 求的长.26. 把函数的图像绕点旋转180°,得到新函数C2的图像,我们称是关于点P的相关函数.C2的图像的对称轴与x轴交点坐标为(t,0).(1)、填空:t的值为(用含m的代数式表示).(2)、若 , 当时,函数C1的最大值为y1 , 最小值为y2 , 且 , 求C2的解析式.(3)、当时,C2的图像与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段原点O逆时针旋转90°,得到它的对应线段 , 若线与C2的图像有公共点,结合函数图象,求a的取值范围.27. 问题背景:如图1,在 中, , , ,四边形 是正方形,求图中阴影部分的面积.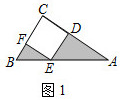 (1)、发现:如图2,小芳发现,只要将 绕点 逆时针旋转一定的角度到达 ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为;(直接写出答案)
(1)、发现:如图2,小芳发现,只要将 绕点 逆时针旋转一定的角度到达 ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为;(直接写出答案)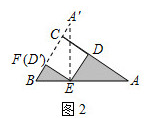 (2)、应用:如图3,在四边形 中, , , 于点 ,若四边形 的面积为16,试求出 的长;
(2)、应用:如图3,在四边形 中, , , 于点 ,若四边形 的面积为16,试求出 的长;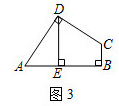 (3)、拓展:如图4,在四边形 中, , , ,以 为顶点作 为 角,角的两边分别交 , 于 , 两点,连接 ,请直接写出线段 , , 之间的数量关系.
(3)、拓展:如图4,在四边形 中, , , ,以 为顶点作 为 角,角的两边分别交 , 于 , 两点,连接 ,请直接写出线段 , , 之间的数量关系.