浙江省宁波市2022-2023学年高一上学期数学期末试卷
试卷更新日期:2023-03-06 类型:期末考试
一、单选题
-
1. 已知全集为 , 集合 , 集合 , 则( )A、 B、 C、 D、2. 函数的零点所在的区间为( )A、 B、 C、 D、3. 已知 , 为非零实数,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 函数的定义域是( )A、 B、 C、 D、5. 已知定义在上的奇函数满足 , 则( )A、-1 B、0 C、1 D、26. 已知 , 则( )A、 B、 C、 D、7. 已知 , , 则( )A、的最大值为且的最大值为 B、的最大值为且的最小值为0 C、的最小值为且的最大值为 D、的最小值为且的最小值为08. 若关于的方程恰有三个不同的实数解 , , , 且 , 其中 , 则的值为( )A、-6 B、-4 C、-3 D、-2
二、多选题
-
9. 下列说法正确的有( )A、若是锐角,则是第一象限角 B、 C、若 , 则为第一或第二象限角 D、若为第二象限角,则为第一或第三象限角10. 关于函数 , 下列说法正确的是( )A、函数定义域为 B、函数是偶函数 C、函数是周期函数 D、函数在区间上单调递减11. 已知且 , 函数的图象可能是( )A、
 B、
B、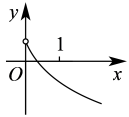 C、
C、 D、
D、 12. 已知实数 , 满足 , 则下列关系式可能正确的是( )A、 , 使 B、 , 使 C、 , 有 D、 , 有
12. 已知实数 , 满足 , 则下列关系式可能正确的是( )A、 , 使 B、 , 使 C、 , 有 D、 , 有三、填空题
-
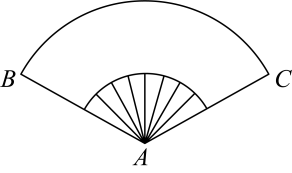
13. 化简求值:.14. 已知函数的图象是一条连续不断的曲线,当时,值域为 , 且在上有两个零点,请写出一个满足上述条件的.15. 炎炎夏日,古代人们乘凉时用的纸叠扇可看作是从一个圆面中剪下的扇形加工制作而成.如图,扇形纸叠扇完全展开后,得到的扇形ABC面积为 , 则当该纸叠扇的周长最小时,的长度为cm.
 16. 已知函数 , 若函数在区间内没有零点,则实数的最大值是.
16. 已知函数 , 若函数在区间内没有零点,则实数的最大值是.四、解答题
-
17. 在①是的充分不必要条件;②;③这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.问题:已知集合 , 集合.(1)、当时,求;(2)、若______,求实数的取值范围.18. 已知函数 , 且 , .(1)、求的值;(2)、若 , , 求.19. 已知函数 , .(1)、若在上有零点,求实数的取值范围;(2)、若在区间上的最小值为-2,求实数的值.20. 已知函数的图象如图所示.
 (1)、求函数的对称中心;(2)、先将函数图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),然后将得到的函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),最后将所得图象向左平移个单位后得到函数的图象.若对任意的恒成立,求实数的取值范围.21. 近年来,受全球新冠肺炎疫情影响,不少外贸企业遇到展会停办、订单延期等困难,在该形势面前,某城市把目光投向了国内大市场,搭建夜间集市,不仅能拓宽适销对路的出口产品内销渠道,助力外贸企业开拓国内市场,更能推进内外贸一体化发展,加速释放“双循环”活力.某夜市的一位文化工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(按30天计),每件的销售价格(单位:元)与时间(单位:天)的函数关系满足(为常数,且),日销售量(单位:件)与时间的部分数据如下表所示:
(1)、求函数的对称中心;(2)、先将函数图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),然后将得到的函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),最后将所得图象向左平移个单位后得到函数的图象.若对任意的恒成立,求实数的取值范围.21. 近年来,受全球新冠肺炎疫情影响,不少外贸企业遇到展会停办、订单延期等困难,在该形势面前,某城市把目光投向了国内大市场,搭建夜间集市,不仅能拓宽适销对路的出口产品内销渠道,助力外贸企业开拓国内市场,更能推进内外贸一体化发展,加速释放“双循环”活力.某夜市的一位文化工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(按30天计),每件的销售价格(单位:元)与时间(单位:天)的函数关系满足(为常数,且),日销售量(单位:件)与时间的部分数据如下表所示:15
20
25
30
105
110
105
100
设该文化工艺品的日销售收入为(单位:元),且第15天的日销售收入为1057元.
(1)、求的值;(2)、给出以下四种函数模型:①;②;③;④.
请你根据上表中的数据,从中选择最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式;
(3)、利用问题(2)中的函数 , 求的最小值.22. 定义在上的函数满足:对任意的 , 都存在唯一的 , 使得 , 则称函数是“型函数”.(1)、判断是否为“型函数”?并说明理由;(2)、若存在实数 , 使得函数始终是“型函数”,求的最小值;(3)、若函数 , 是“型函数”,求实数的取值范围.