广西北海市2022-2023学年高一上学期数学期末教学质量检测试卷

试卷更新日期：2023-03-06 类型：期末考试

进入出卷网下载

一、单选题

1. 命题“ $\forall x \in R$ ， $x^{2} > 1 - 2 x$ ”的否定是（）

A、 $\forall x \in R$ ， $x^{2} < 1 - 2 x$ B、 $\forall x \in R$ ， $x^{2} \leq 1 - 2 x$ C、 $\exists x \in R$ ， $x^{2} \leq 1 - 2 x$ D、 $\exists x \in R$ ， $x^{2} < 1 - 2 x$

查看试题解析
2. 函数 $f (x) = \frac{1}{\sqrt{2 - x}} + x^{0}$ 的定义域是（）

A、 $(- \infty ， 2]$ B、 $(0 ， 2)$ C、 $(- \infty ， 0) ∪ (0 ， 2)$ D、 $(- \infty ， 0) \cup (0 ， 2]$

查看试题解析
3. 函数 $f (x) = \frac{x^{2} + | x |}{2^{x} + 2^{- x}}$ 部分图像大致是（）

A、 B、 C、 D、

查看试题解析
4. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间 $[0 ， 10]$ 内的一个数来表示，该数越接近10表示满意程度越高，现随机抽取7位小区居民，他们的幸福感指数分别为5，6，7，8，9，5，4，则这组数据的第60百分位数是（）

A、7 B、7.5 C、8 D、9

查看试题解析
5. 已知 $a = 2 l o g_{3} 2 \sqrt{2}$ ， $b = 0 . 3^{0.01}$ ， $c = l o g_{\sqrt{2}} 2$ ，则a，b，c的大小关系为（）

A、 $a < b < c$ B、 $b < a < c$ C、 $c < a < b$ D、 $a < c < b$

查看试题解析
6. 某中学有高中生1800人，初中生1200人，为了解学生课外锻炼情况，用分层抽样的方法从学生中抽取一个容量为 $n$ 的样本.已知从高中生中抽取的人数比从初中生中抽取的人数多24，则 $n =$ （）

A、48 B、72 C、60 D、120

查看试题解析
7. 已知 $a ， b$ 为正实数，以下不等式成立的有（）
① $\frac{b}{a} > \frac{b + 1}{a + 1}$ ；② $a b + \frac{2}{a b} > 2$ ；③ $a^{2} + b^{2} > 4 a b - 4 b^{2}$ ；④ $| a - 1 | + | a | \geq 1$

A、②④ B、②③ C、②③④ D、①④

查看试题解析
8. 牛顿冷却定律描述物体在常温环境下的温度变化：如果物体的初始温度为 $T_{0}$ ，则经过一定时间t分钟后的温度T满足 $T - T_{a} = {(\frac{1}{2})}^{\frac{t}{h}} (T_{0} - T_{a})$ ， h称为半衰期，其中 $T_{a}$ 是环境温度．若 $T_{a} = 25$ ℃，现有一杯80℃的热水降至75℃大约用时1分钟，那么水温从75℃降至45℃，大约还需要（参考数据： $l g 2 \approx 0.30$ ， $l g 11 \approx 1.04$ ）（）

A、9分钟 B、10分钟 C、11分钟 D、12分钟

查看试题解析

二、多选题

9. 当 $x \in (0 ， 1)$ 时，幂函数 $y = x^{a}$ 的图像在直线 $y = x$ 的上方，则 $a$ 的值可能为（）

A、 $\frac{1}{3}$ B、 $- 2$ C、 $\sqrt{2}$ D、3

查看试题解析
10. 5月6日，小明同学因发热而住院，下图是根据护士为他测量的体温所绘制的体温折线图.根据图中的信息可得（）

A、护士每隔6小时给小明测量一次体温 B、近三天来，小明所测体温数据的极差为3.7摄氏度 C、近三天来，小明所测体温数据的中位数是37.5摄氏度 D、如果连续36小时体温不超过37.2摄氏度的话，可认为基本康复，可以出院，那么小明最快5月10日凌晨6时出院

查看试题解析
11. 某工厂制造一种零件，甲机床的正品率是0.7，乙机床的正品率为0.8，分别从它们制造的产品中任意抽取一件，则（）

A、两件都是次品的概率为0.06 B、事件“至多有一件正品”与事件“至少有一件正品”是互斥事件 C、恰有一件正品的概率为0.38 D、事件“两件都是次品”与事件“至少有一件正品”是对立事件

查看试题解析
12. 已知函数 $f (x) = l n (\sqrt{x^{2} + 1} + x) + x + 1$ .则下列说法正确的是（）

A、 $f (l g 3) + f (l g \frac{1}{3}) = 2$ B、函数 $f (x)$ 的图象关于点 $(0 ， 1)$ 对称 C、函数 $f (x)$ 在定义域上单调递减 D、若实数a，b满足 $f (a) + f (b) > 2$ ，则 $a + b > 0$

查看试题解析

三、填空题

13. 某中学为了加强艺术教育，促进学生全面发展，要求每名学生从音乐和美术中至少选择一门兴趣课，某班有50名学生，选择音乐的有21人，选择美术的有39人，从全班学生中随机抽取一人，那么这个人两种兴趣班都选择的概率是.

查看试题解析
14. 若函数 $f (x) = 2 x + m$ 在区间 $(1 ， 2)$ 上存在一个零点，则实数m的取值范围是.

查看试题解析
15. 已知 $p ： x^{2} - 8 x + 15 < 0$ ， $q ： (x - 2 m) (x - 5 m) < 0$ ，其中 $m > 0$ .若 $q$ 是 $p$ 的必要不充分条件，则实数 $m$ 的取值范围是.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} | x + 2 | ， x \leq - 1 ， \\ l n | x | ， x > - 1 且 x \neq 0 . \end{array}$ 若方程 $f (x) - m = 0 (m \in R)$ 恰有三个不同的实数根 $x_{1} ， x_{2} ， x_{3} (x_{1} < x_{2} < x_{3})$ ，则 $m$ 的取值范围是， $(x_{1} + x_{2}) \cdot x_{3}$ 的取值范围是.

查看试题解析

四、解答题

17. 已知全集 $U = R$ ，集合 $A = {x \in R | - 5 \leq 3 x - 2 \leq 1}$ ，集合 $B = {x \in R | l o g_{2} (2 - x) \leq 1}$ .

(1)、求 $A \cap B$ ， $A \cup B$ ；

(2)、求 $(∁_{R} B) \cup A$ .

查看试题解析
18.

(1)、计算： $l o g_{2} 25 \times l o g_{3} 4 \times l o g_{5} 9$ ；

(2)、求满足 $l o g_{2} [l o g_{3} (l o g_{4} x)] = 0$ 的x的值.

查看试题解析
19. 已知 $m + 2 n = 2$ ．

(1)、当 $m > 0$ ， $n > 0$ 时，求 $\frac{1}{m} + \frac{2}{n}$ 的最小值；

(2)、当 $m > - 1$ ， $n > 0$ 时，求 $\frac{1}{m + 1} + \frac{2}{n}$ 的最小值．

查看试题解析
20. 已知函数 $f (x) = (a^{2} - 5 a + 7) \cdot {(a - 1)}^{x}$ 是指数函数.

(1)、求实数 $a$ 的值；

(2)、已知 $g (x) = f^{2} (x) - 2 f (x) + 3$ ， $x \in [- 1 ， 2]$ ，求 $g (x)$ 的值域.

查看试题解析
21. 读书可以增长知识，开拓视野，修身怡情.树人中学为了解本校学生课外阅读情况，按性别进行分层，用分层随机抽样的方法从全校学生中抽出一个容量为100的样本，其中男生40名，女生60名.经调查统计，分别得到40名男生一周课外阅读时间（单位：小时）的频数分布表和60名女生一周课外阅读时间（单位：小时）的频率分布直方图.
男生一周阅读时间频数分布表
小时
频数
$[0 ， 2)$
9
$[2 ， 4)$
25
$[4 ， 6)$
3
$[6 ， 8)$
3

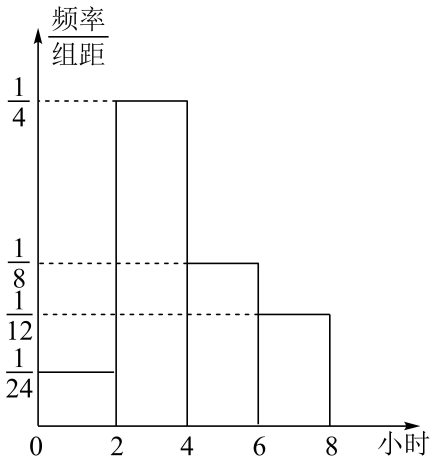(1)、由以上频率分布直方图估计该校女生一周阅读时间的众数和75%分位数；

(2)、由以上频数分布表和频率分布直方图估计总样本的平均数 $\bar{z}$ ；

(3)、从一周课外阅读时间为 $[4 ， 6)$ 的样本学生中按比例分配抽取6人，再从这6人中任意抽取2人，求恰好抽到一男一女的概率.
（注：以各组的区间中点值代表该组的各个值）

查看试题解析
22. 已知函数 $f (x) = \frac{2^{x} + a}{2^{x} - a}$ 为奇函数，其中 $a \in R$ 且 $a < 0$ .

(1)、求实数a的值，判断并证明函数 $f (x)$ 的单调性；

(2)、函数 $f (x)$ 在区间 $[m ， n] (m < n)$ 上的值域是 $[k \cdot 2^{m} ， k \cdot 2^{n}] (k \in R)$ ，求k的取值范围.

查看试题解析

男生一周阅读时间频数分布表
小时	频数
$[0 ， 2)$	9
$[2 ， 4)$	25
$[4 ， 6)$	3
$[6 ， 8)$	3