备战2023年中考数学细点逐一突破真题训练第8章反比例函数
试卷更新日期:2023-03-06 类型:二轮复习
一、反比例函数基本概念与性质
-
1. 如果函数反比例函数,那么m的值是( )A、2 B、-1 C、1 D、02. 下列关于反比例函数 ( )的说法中,正确的是( )A、双曲线在第一、第三象限 B、当 时,函数值 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小3. 已知函数是关于x的反比例函数,则该函数图象位于( )A、第一、第三象限 B、第二、第四象限 C、第一、第二象限 D、第三、第四象限4. 从-1,2,-3,4这四个数中任取两个不同的数分别作为a,b的值,得到反比例函数 ,则这些反比例函数中,其图象在二、四象限的概率是 .
二、反比例函数图像共存问题
-
5. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
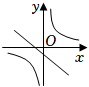 B、
B、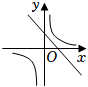 C、
C、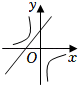 D、
D、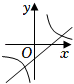 6. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
6. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )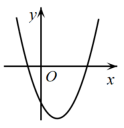 A、
A、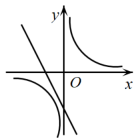 B、
B、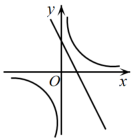 C、
C、 D、
D、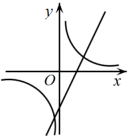
三、反比例函数图像性质
-
7. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、8. 在反比例函数(k为常数)的图象上有三个点(-3,y1),(-1,y2), , 则函数值y1 , y2 , y3的大小关系为( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y3<y1<y29. 在反比例函数 ( 为常数)上有三点 , , ,若 ,则 , , 的大小关系为( )A、 B、 C、 D、10. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、11. 若点 、 、 都在反比例函数 (k为常数)的图象上,则 、 、 的大小关系为 .
四、反比例函数系数K几何特性
-
12. 如图,两个反比例函数y1=和y2=在第一象限内的图象分别是C1和C2 , 设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
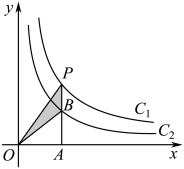 A、4 B、2 C、1 D、613. 如图,在反比例函数 (x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( )
A、4 B、2 C、1 D、613. 如图,在反比例函数 (x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( )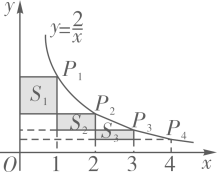 A、1 B、 C、 D、2
A、1 B、 C、 D、2五、反比例函数与方程,不等式结合
-
14. 如图,正比例函数与反比例函数的图象交于、B两点,当时,x的取值范围是( )
 A、或 B、或 C、或 D、或15. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .
A、或 B、或 C、或 D、或15. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .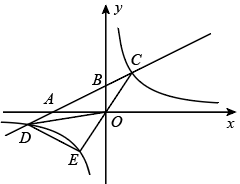 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.16. 反比例函数 的图象如图所示,一次函数 y=kx+b(k≠0)的图象与 的图象交于A (m, 4),B(-2,n)两点,
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.16. 反比例函数 的图象如图所示,一次函数 y=kx+b(k≠0)的图象与 的图象交于A (m, 4),B(-2,n)两点,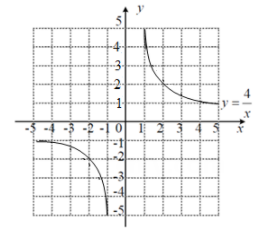 (1)、求一次函数的表达式,并在所给的平面直角坐标系中面出该函数的图象;(2)、观察图象,直接写出不等式 的解集;(3)、一次函数y=kx+b的图象与 x 轴交于点 C,连接 OA,求△OAC 的面积.
(1)、求一次函数的表达式,并在所给的平面直角坐标系中面出该函数的图象;(2)、观察图象,直接写出不等式 的解集;(3)、一次函数y=kx+b的图象与 x 轴交于点 C,连接 OA,求△OAC 的面积.六、反比例函数解析式确定
-
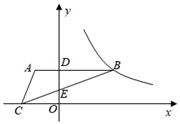
17. 在平面直角坐标系中,将点向下平移5个单位长度得到点 , 若点恰好在反比例函数的图象上,则的值是.18. 如图, 的顶点B在反比例函数 的图象上,顶点C在x轴负半轴上, 轴,AB , BC分别交y轴于点D , E . 若 , ,则 .
 19. 若反比例函数y= 的图象经过点(﹣2,3),则k= .20. 如图,在平面直角坐标系中,函数 y=kx 与 y=的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数的图象于点 C,连接 BC,则△ABC 的面积为( )
19. 若反比例函数y= 的图象经过点(﹣2,3),则k= .20. 如图,在平面直角坐标系中,函数 y=kx 与 y=的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数的图象于点 C,连接 BC,则△ABC 的面积为( )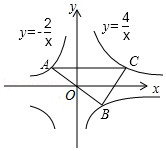 A、2 B、4 C、6 D、821. 如图,AB⊥x轴,B为垂足,双曲线(x>0)与△AOB的两条边OA,AB分别相交于C,D两点,OC=CA,△ACD的面积为3,则k等于( )
A、2 B、4 C、6 D、821. 如图,AB⊥x轴,B为垂足,双曲线(x>0)与△AOB的两条边OA,AB分别相交于C,D两点,OC=CA,△ACD的面积为3,则k等于( )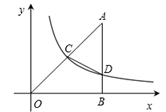 A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6七、反比例函数与特殊四边形结合
-
22. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O, 于E点,交BD于M点,反比例函数 的图象经过线段DC的中点N,若 ,则ME的长为( )
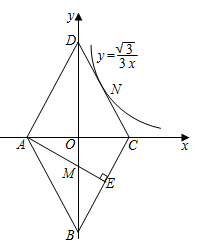 A、 B、 C、 D、23. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )
A、 B、 C、 D、23. 如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图像过点C,则k的值为( )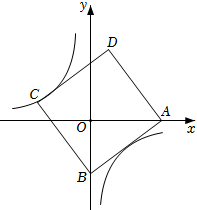 A、4 B、﹣4 C、﹣3 D、324. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )
A、4 B、﹣4 C、﹣3 D、324. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )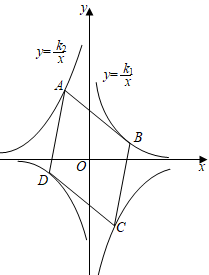 A、 B、 C、 D、25. 反比例函数和的图象如图,点A,C分别是x轴、y轴上的点,四边形是正方形, , 分别与反比例函数 , 的图象交于点F,H和点E,G,若 , 则的值为( )
A、 B、 C、 D、25. 反比例函数和的图象如图,点A,C分别是x轴、y轴上的点,四边形是正方形, , 分别与反比例函数 , 的图象交于点F,H和点E,G,若 , 则的值为( )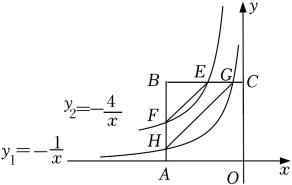 A、 B、 C、 D、26. 如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
A、 B、 C、 D、26. 如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.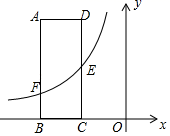 (1)、若点B坐标为(﹣6,0),求直线AE的表达式;(2)、反比例函数y=(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;(3)、在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.
(1)、若点B坐标为(﹣6,0),求直线AE的表达式;(2)、反比例函数y=(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;(3)、在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.八、反比例函数与一次函数结合
-
27. 如图,正比例函数与反比例函数的图象交于 , 两点.
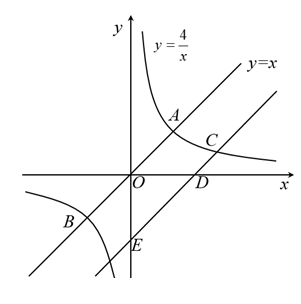 (1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.28. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .
(1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.28. 如图,一次函数的图像与反比例函数的图像交于点 , 与轴交于点 , 与轴交于点 , 轴于点 , , 点关于直线的对称点为点 .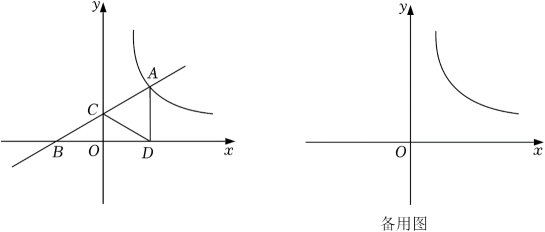 (1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.
(1)、点是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.①求、的值;
②若点在轴上,当最大时,求点的坐标.
29. 如图,在平面直角坐标系中,菱形的顶点在轴上, , 两点的坐标分别为 , , 直线:与反比例函数的图象交于 , 两点.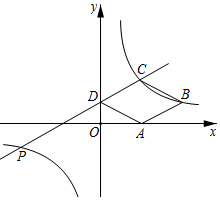 (1)、求该反比例函数的解析式及的值;(2)、判断点是否在该反比例函数的图象上,并说明理由.30. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 两点.
(1)、求该反比例函数的解析式及的值;(2)、判断点是否在该反比例函数的图象上,并说明理由.30. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于 两点.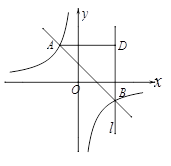 (1)、求反比例函数和一次函数的解析式;(2)、过点 作直线 ∥ 轴,过点 作直线 于 ,点 是直线 上一动点,若 ,求点 的坐标.31. 如图一次函数的图象与坐标轴相交于点和点B,与反比例函数的图象相交于点 .
(1)、求反比例函数和一次函数的解析式;(2)、过点 作直线 ∥ 轴,过点 作直线 于 ,点 是直线 上一动点,若 ,求点 的坐标.31. 如图一次函数的图象与坐标轴相交于点和点B,与反比例函数的图象相交于点 .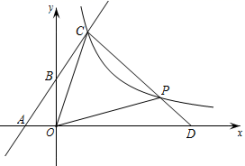 (1)、求出一次函数与反比例函数的解析式;(2)、若点P是反比例函数图象上的一点,连接并延长,交x轴正半轴于点D,若时,求的面积;(3)、在(2)的条件下,在y轴上是否存在点Q,使的值最小,若存在请直接写出的最小值,若不存在请说明理由.
(1)、求出一次函数与反比例函数的解析式;(2)、若点P是反比例函数图象上的一点,连接并延长,交x轴正半轴于点D,若时,求的面积;(3)、在(2)的条件下,在y轴上是否存在点Q,使的值最小,若存在请直接写出的最小值,若不存在请说明理由.九、反比例函数生活应用
-
32. 为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.
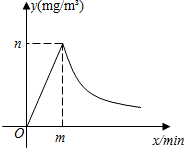 (1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.33. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“嗐转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,y与x之间有如表关系:
(1)、校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.33. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“嗐转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,y与x之间有如表关系:厘米
1
2
3
5
米
14
7
2.8
请根据表中的信息解决下列问题:
(1)、求出y与x之间的函数解析式;(2)、若某人蒙上眼睛走出的大圆圈的半径为35米,则其两腿迈出的步长之差是多少厘米?34. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示. (1)、求这个反比例函数的解析式,并直接写出蓄电池的电压值(单位:v)(2)、如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?
(1)、求这个反比例函数的解析式,并直接写出蓄电池的电压值(单位:v)(2)、如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?