沪科版数学七年级下册7.3 一元一次不等式组同步练习
试卷更新日期:2023-03-04 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 若不等式组的解集是x<2,则m的取值范围是( )A、m=2 B、m≥2 C、m<2 D、m>22. 不等式组的最小整数解为( )A、 B、 C、 D、3. 不等式组的解集在数轴上用阴影表示正确的是( )A、
 B、
B、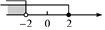 C、
C、 D、
D、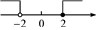 4. 如图是测量一颗玻璃球体积的过程:
4. 如图是测量一颗玻璃球体积的过程:
(1)将的水倒进一个容量为的杯子中;
(2)将五颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,推测这样一颗玻璃球的体积范围是( )
A、以上,以下 B、以上,以下 C、以上,以下 D、以上,以下5. 若不等式组的解集为1<x<2,则(m+n)2022的值为( )A、-1 B、0 C、1 D、26. 若关于x的一元一次不等式组 有解,则m的取值范围为( )A、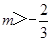 B、
B、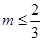 C、
C、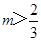 D、
D、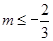 7. 若关于x的不等式组无解,则实数a的取值范围是( )A、a<-4 B、a=-4 C、a>-4 D、a≥-48. 已知关于的不等式组的整数解只有3个,则的取值范围是( )A、 B、 C、 D、9. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
7. 若关于x的不等式组无解,则实数a的取值范围是( )A、a<-4 B、a=-4 C、a>-4 D、a≥-48. 已知关于的不等式组的整数解只有3个,则的取值范围是( )A、 B、 C、 D、9. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( ) A、 B、 C、 D、10. 若整数 使关于 的不等式组 有解,且使关于 , 的方程组 的解为正整数,那么所有满足条件的整数 的值的积是( )A、0 B、-80 C、40 D、80
A、 B、 C、 D、10. 若整数 使关于 的不等式组 有解,且使关于 , 的方程组 的解为正整数,那么所有满足条件的整数 的值的积是( )A、0 B、-80 C、40 D、80二、填空题(每题2分,共8分)
-
11. 不等式组的解集是 .12. 要使方程组有正整数解,则整数a有个.13. 已知关于 , 的方程组 的解满足 , 则的取值范围是 .14. 有一个长方体水箱,从里面量得它的深度为 , 底面长为 , 宽为 , 水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块,则水箱的水深为.
三、计算题(共2题,共18分)
-
15. 简答(1)、解不等式组: , 并把解集在数轴上表示出来.
 (2)、计算:16. 解一元一次不等式组 , 并把解表示在数轴上.
(2)、计算:16. 解一元一次不等式组 , 并把解表示在数轴上.
四、解答题(共4题,共44分)
-
17. 如果一个一元一次方程的解在一个一元一次不等式(组)的解集范围内,则称该一元一次方程为该不等式(组)的关联方程.例:方程是不等式的关联方程.(1)、试判断方程是下列哪个不等式的关联方程①; ②;
③;请直接写出序号 .
(2)、若关于的方程是不等式组的关联方程,求的取值范围.(3)、若方程 , 都是关于的不等式组的关联方程且不等式组的整数解有3个,求的取值范围.18. 已知:关于、的方程组:(1)、求这个方程组的解:(用含有字母的代数式表示)(2)、若这个方程组的解满足为非负数,为负数,求字母的取值范围19. 在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)、求每台电脑、每台电子白板各多少万元?(2)、根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.20. 随着全国疫情防控取得阶段性进展,各学校进一步做好疫情防控工作.为方便师生测体温,某校计划购买A、B两种额温枪.经调研得知:购买1个A型额温枪和2个B型额温枪共需800元,购买2个A型额温枪和3个B型额温枪共需1300元.(1)、求每个A型额温枪和B型额温枪各多少元;(2)、若该学校准备购买A、B两种型号的额温枪共50个(每种型号至少买一只);要求总费用不超过12800元,则对购买A型号的额温枪在数量上有什么要求?说明理由.(3)、在(2)的条件下,若甲、乙两商店以同样价格出售这两种型号的额温枪,同时又各自推出不同的优惠方案:在甲店购买A型额温枪按原价90%收费,B型额温枪不优惠;在乙店购买A型额温枪不优惠,但购买B型额温枪按原价90%收费;则学校到哪家商店购买额温枪花费少?