2023年中考数学精选真题实战测试58 图形变换 B
试卷更新日期:2023-03-04 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若点与点关于y轴对称,则的值是( )A、-1 B、-3 C、1 D、23. 如图,将直角三角板ABC绕顶点A顺时针旋转到△AB'C',点B’恰好落在CA的延长线上,∠B=30°,∠C=90°,则∠BAC'为( )
2. 若点与点关于y轴对称,则的值是( )A、-1 B、-3 C、1 D、23. 如图,将直角三角板ABC绕顶点A顺时针旋转到△AB'C',点B’恰好落在CA的延长线上,∠B=30°,∠C=90°,则∠BAC'为( )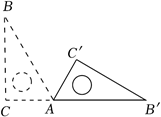 A、90° B、60° C、45° D、30°4. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、90° B、60° C、45° D、30°4. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、5. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )
A、 B、 C、 D、5. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )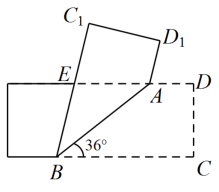 A、48° B、66° C、72° D、78°6. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
A、48° B、66° C、72° D、78°6. 如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( ) A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)7. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
A、(4,0) B、(2,﹣2) C、(4,﹣1) D、(2,﹣3)7. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( ) A、9 B、12 C、15 D、188. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )
A、9 B、12 C、15 D、188. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )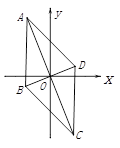 A、 B、 C、 D、9. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )
A、 B、 C、 D、9. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )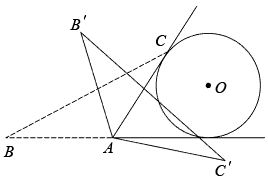 A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每空3分,共18分)
-
11. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
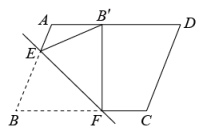 12. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .
12. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .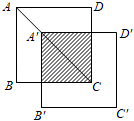 13. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
13. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .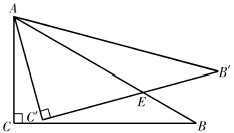 14. 在平面直角坐标系中,Q是直线 上的一个动点,将Q绕点 顺时针旋转 ,得到点 连接 ,则 的最小值为 .
14. 在平面直角坐标系中,Q是直线 上的一个动点,将Q绕点 顺时针旋转 ,得到点 连接 ,则 的最小值为 .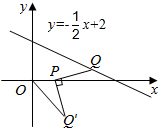 15. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).
15. 如图,已知等腰的顶角的大小为 , 点D为边上的动点(与、不重合),将绕点A沿顺时针方向旋转角度时点落在处,连接.给出下列结论:①;②;③当时,的面积取得最小值.其中正确的结论有(填结论对应的序号).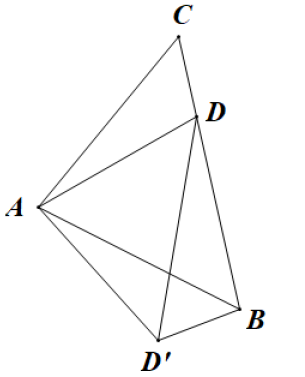 16. 如图,菱形ABCD中,对角线AC,BD相交于点O, , , AH是的平分线,于点E,点P是直线AB上的一个动点,则的最小值是 .
16. 如图,菱形ABCD中,对角线AC,BD相交于点O, , , AH是的平分线,于点E,点P是直线AB上的一个动点,则的最小值是 .
三、解答题(共7 题,共72分)
-
17. 如图1,在中,于点D,在DA上取点E,使 , 连接BE、CE.
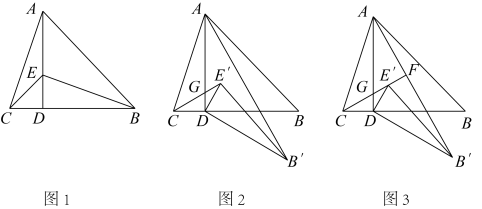 (1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.18. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;
(1)、直接写出CE与AB的位置关系;(2)、如图2,将绕点D旋转,得到(点 , 分别与点B,E对应),连接 , 在旋转的过程中与的位置关系与(1)中的CE与AB的位置关系是否一致?请说明理由;(3)、如图3,当绕点D顺时针旋转30°时,射线与AD、分别交于点G、F,若 , 求的长.18. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;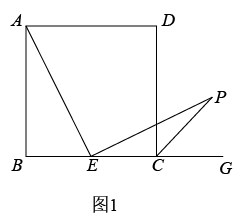
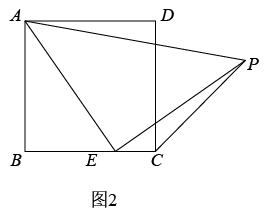
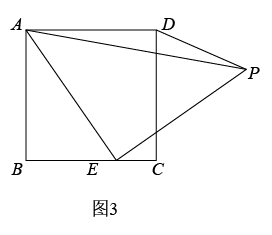 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.19. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.19. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.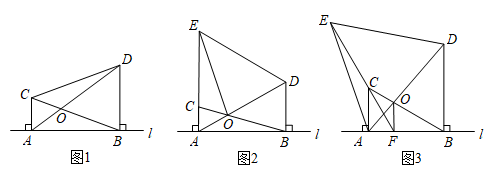 (1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.
(1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.①如图2,当与重合时,连接 , 若 , 求的长;
②如图3,当时,连接并延长交直线l于点F,连接.求证:.
20. 如图,在中, , , 点在直线上,连接 , 将BD绕点逆时针旋转 , 得到线段 , 连接 , . (1)、求证:;(2)、当点在线段上(点不与点 , 重合)时,求的值;(3)、过点作交于点 , 若 , 请直接写出的值.21. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 .
(1)、求证:;(2)、当点在线段上(点不与点 , 重合)时,求的值;(3)、过点作交于点 , 若 , 请直接写出的值.21. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 . (1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.22. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形 和等腰直角三角形 ,按如图1的方式摆放, ,随后保持 不动,将 绕点C按逆时针方向旋转 ( ),连接 , ,延长 交 于点F,连接 .该数学兴趣小组进行如下探究,请你帮忙解答:
(1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.22. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形 和等腰直角三角形 ,按如图1的方式摆放, ,随后保持 不动,将 绕点C按逆时针方向旋转 ( ),连接 , ,延长 交 于点F,连接 .该数学兴趣小组进行如下探究,请你帮忙解答:

【初步探究】
(1)、如图2,当 时,则 ;(2)、如图3,当点E,F重合时,请直接写出 , , 之间的数量关系:;(3)、如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.(4)、如图5,在 与 中, ,若 , (m为常数).保持 不动,将 绕点C按逆时针方向旋转 ( ),连接 , ,延长 交 于点F,连接 ,如图6.试探究 , , 之间的数量关系,并说明理由.23. 综合与实践 (1)、知识再现
(1)、知识再现
如图 , 中, , 分别以、、为边向外作的正方形的面积为、、 . 当 , 时, .(2)、问题探究如图,中, .
如图 , 分别以、、为边向外作的等腰直角三角形的面积为、、 , 则、、之间的数量关系是 .(3)、如图 , 分别以、、为边向外作的等边三角形的面积为、、 , 试猜想、、之间的数量关系,并说明理由.(4)、实践应用
如图4,将图中的绕点逆时针旋转一定角度至 , 绕点顺时针旋转一定角度至 , 、相交于点 . 求证:;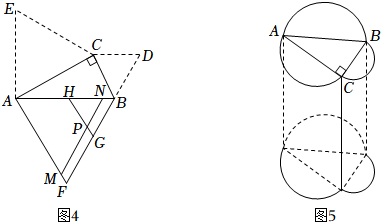 (5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.
(5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.