陕西省宝鸡市金台区2022-2023学年高二上学期理数期末试卷

试卷更新日期：2023-03-03 类型：期末考试

进入出卷网下载

一、单选题

1. 命题“ $\forall x \in R ， x^{2} - 2 x + 1 \geq 0$ ”的否定为（）

A、 $\forall x \in R ， x^{2} - 2 x + 1 < 0$ B、 $\forall x \notin R ， x^{2} - 2 x + 1 \geq 0$ C、 $\exists x \in R ， x^{2} - 2 x + 1 \geq 0$ D、 $\exists x \in R ， x^{2} - 2 x + 1 < 0$

查看试题解析
2. 抛物线 $y = 4 x^{2}$ 的焦点坐标为（）

A、 $(0 ， \frac{1}{8})$ B、 $(0 ， \frac{1}{16})$ C、 $(\frac{1}{16} ， 0)$ D、 $(\frac{1}{8} ， 0)$

查看试题解析
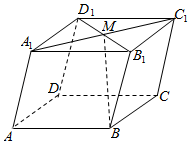
3. 命题“若 $x y = 0,$ 则 $x = 0 (x, y \in R)$ ”的逆命题、否命题、逆否命题三个命题中，真命题的个数为（）

A、3 B、2 C、1 D、0

查看试题解析
4. 已知命题 $p ： \frac{1}{x} < 1$ ，命题 $q ： x > 1$ ，则 $p$ 是 $q$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
5. 已知 $\vec{a} = (2 ， 3 ， - 1) ， \vec{b} = (2 ， 0 ， - 4) ， \vec{c} = (- 4 ， - 6 ， 2)$ ，则下列结论正确的是（）

A、 $\vec{a} ⊥ \vec{b}$ B、 $\vec{a} ⊥ \vec{c}$ C、 $\vec{a} / / \vec{b}$ D、 $\vec{a} / / \vec{c}$

查看试题解析
6. 已知命题 $p$ ：离心率越小，椭圆的形状越扁，命题 $q$ ：离心率越大，双曲线的“张口”越小，则下列命题为真命题的是（）

A、 $(\neg p) \land q$ B、 $(\neg p) \lor q$ C、 $p \lor q$ D、 $p \land q$

查看试题解析
7. 如图所示，在平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，M为 $A_{1} C_{1}$ 与 $B_{1} D_{1}$ 的交点，若 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ， $\vec{A A_{1}} = \vec{c}$ ，则 $\vec{B M} =$ （）

A、 $\frac{1}{2} \vec{a} - \frac{1}{2} \vec{b} + \vec{c}$ B、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \vec{c}$ C、 $- \frac{1}{2} \vec{a} - \frac{1}{2} \vec{b} + \vec{c}$ D、 $- \frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \vec{c}$

查看试题解析
8. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = B C = 1$ ， $A A_{1} = \sqrt{3}$ ，则异面直线 $A D_{1}$ 与 $D B_{1}$ 所成角的余弦值为（）

A、 $\frac{1}{5}$ B、 $\frac{\sqrt{5}}{6}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
9. 已知 $\vec{v}$ 为直线 $l$ 的方向向量， $\vec{n_{1}}$ ， $\vec{n_{2}}$ 分别为平面 $α$ ， $β$ 的法向量 $(α ， β$ 不重合 $)$ ，那么下列说法中：① $\vec{n_{1}} / / \vec{n_{2}} \Leftrightarrow α / / β$ ；② $\vec{n_{1}} ⊥ \vec{n_{2}} \Leftrightarrow α ⊥ β$ ；③ $\vec{v} / / \vec{n_{1}} \Leftrightarrow l / / α$ ；④ $\vec{v} ⊥ \vec{n_{1}} \Leftrightarrow l ⊥ α .$ 正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 若点P在椭圆 $C ： \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 上， $F_{1}$ ， $F_{2}$ 分别为椭圆C的左右焦点，且 $∠ F_{1} P F_{2} = 60 °$ ，则 $△ F_{1} P F_{2}$ 的面积为（）．

A、 $\sqrt{3}$ B、3 C、4 D、1

查看试题解析
11. 如图是一水平放置的青花瓷．它的外形为单叶双曲面，可看成是双曲线的一部分绕其虚轴旋转所形成的曲面，且其外形上下对称．花瓶的最小直径为 $12 cm$ ，瓶口直径为 $20cm$ ，瓶高为 $30 cm$ ，则该双曲线的虚轴长为（）

A、 $\frac{45}{8}$ B、 $\frac{45}{4}$ C、 $\frac{45}{2}$ D、45

查看试题解析
12. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 左右焦点分别为 $F_{1} ， F_{2}$ ，上顶点为A，离心率为 $\frac{1}{2}$ ，过 $F_{1}$ 且为线段 $A F_{2}$ 的垂线 $l$ 交 $C$ 于 $M ， N$ 两点，则 $△ A M N$ 周长为（）

A、 $4 a$ B、 $3 a$ C、 $2 a$ D、 $2 a + 2 c$

查看试题解析

二、填空题

13. 若方程 $\frac{x^{2}}{5 - m} + \frac{y^{2}}{m - 3} = 1$ 表示焦点在 $x$ 轴上的椭圆，则实数 $m$ 的取值范围为．

查看试题解析
14. 双曲线 $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$ 的焦点到其渐近线的距离是.

查看试题解析
15. 在长方体 $A B C D - A^{'} B^{'} C^{'} D^{'}$ 中， $A A^{'} = 2 A B = 2 A D = 2$ ，以点 $D$ 为坐标原点，以 $D A ， D C ， D D^{'}$ 分别为 $x$ 轴， $y$ 轴， $z$ 轴建立空间直角坐标系，设对角面 $A C D^{'}$ 所在法向量为 $(x ， y ， z)$ ，则 $x ： y ： z =$ ．

查看试题解析
16. 设 $F_{1} ， F_{2}$ 为双曲线 $\frac{x^{2}}{4} - y^{2} = 1$ 的两个焦点，关于原点对称的两点 $P ， Q$ 都在双曲线上，且满足 $| P Q | = | F_{1} F_{2} |$ ，则四边形 $F_{1} P F_{2} Q$ 的面积为．

查看试题解析

三、解答题

17. 已知命题p：实数x满足 $x^{2} - 7 x + 10 \leq 0 ，$ 命题q：实数x满足 $x^{2} - 4 m x + 3 m^{2} \leq 0 .$ 其中m> 0.

(1)、若m=4且命题p， q都为真命题，求实数x的取值范围；

(2)、若p是q的充分不必要条件，求实数m的取值范围.

查看试题解析
18. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的两焦点分别为 $F_{1} (- 2 ， 0) ， F_{2} (2 ， 0)$ ，且经过点 $(- \frac{5}{2} ， \frac{3}{2})$ ．

(1)、求椭圆 $C$ 的方程；

(2)、设过椭圆的右焦点 $F_{2}$ 且斜率为 $\frac{\sqrt{3}}{3}$ 的直线 $l$ 交椭圆 $C$ 于 $P ， Q$ 两点，求 $△ P O Q$ 的面积．

查看试题解析
19. 如图在四棱锥 $P - A B C D$ 中， $P D ⊥$ 平面 $A B C D ， E$ 为 $A D$ 的中点，底面 $A B C D$ 是边长为2的正方形，且平面 $P E B$ 与平面 $A B C D$ 夹角的余弦值为 $\frac{\sqrt{6}}{6}$ ．

(1)、求棱 $P D$ 的长；

(2)、求点 $C$ 到平面 $P E B$ 的距离．

查看试题解析
20. 点 $M$ 到点 $F (4 ， 0)$ 的距离比它到直线 $l ： x + 6 = 0$ 的距离小2，记动点 $M$ 的轨迹为 $C$ ．

(1)、求 $C$ 的方程；

(2)、若过点 $F$ 的直线 $m$ 交曲线 $C$ 于 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 两点，求 $\frac{1}{| A F |} + \frac{1}{| B F |}$ 的值．

查看试题解析
21. 已知 $F_{1} (- a ， 0) ， F_{2} (a ， 0)$ ，其中 $a > 0$ ，动点 $M (x ， y)$ 满足直线 $M F_{1}$ 与 $M F_{2}$ 斜率之积等于 $λ （ λ \neq 0 ）$ ，试讨论动点 $M$ 的轨迹 $C$ 的形状．

查看试题解析
22. 如图，在三棱锥 $S - A B C$ 中， $A B = A C = 2$ ， $S A = S B = S C = 3 \sqrt{2}$ ， $B C = 2 \sqrt{2}$ ， $D$ 为 $B C$ 的中点.

(1)、证明： $S D ⊥$ 平面ABC；

(2)、若E是棱AC上的动点，当 $△ S D E$ 的面积最小时，求SC与平面SDE所成角的余弦值.

查看试题解析