备战2023年中考数学细点逐一突破真题训练第7章一次函数
试卷更新日期:2023-03-02 类型:二轮复习
一、函数的基本概念
-
1. 如图所示图象表示的两个变量间的关系中,y不是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 2. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且3. 已知函数y=(m﹣2)+1是一次函数,则m的值为( )A、± B、 C、±2 D、﹣24. 函数 , , , , ,其中一次函数的个数有个.
2. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且3. 已知函数y=(m﹣2)+1是一次函数,则m的值为( )A、± B、 C、±2 D、﹣24. 函数 , , , , ,其中一次函数的个数有个.二、一次函数的图像性质
-
5. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、
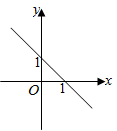 B、
B、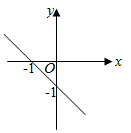 C、
C、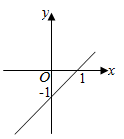 D、
D、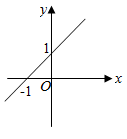 6. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、7. 一次函数y=3x+b(b≥0)的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
6. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、7. 一次函数y=3x+b(b≥0)的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、 B、
B、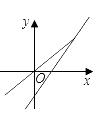 C、
C、 D、
D、 9. 将直线 向左平移 ( )个单位后,经过点(1,−3),则 的值为.10. 已知一次函数的图象与直线 平行,且过点 ,求该一次函数的表达式.11. 如果不论k为何值,一次函数y= 的图象都经过一定点, 则该定点的坐标是 .
9. 将直线 向左平移 ( )个单位后,经过点(1,−3),则 的值为.10. 已知一次函数的图象与直线 平行,且过点 ,求该一次函数的表达式.11. 如果不论k为何值,一次函数y= 的图象都经过一定点, 则该定点的坐标是 .三、分析函数图像
-
12. 小丽从甲地匀速步行去乙地,小华骑自行车从乙地匀速前往甲地,同时出发,两人离甲地的距离(m)与出发时间(min)之间的函数关系如图所示.
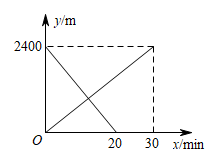 (1)、小丽步行的速度为m/min;(2)、当两人相遇时,求他们到甲地的距离.13. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( )
(1)、小丽步行的速度为m/min;(2)、当两人相遇时,求他们到甲地的距离.13. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( ) A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地14. 为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地14. 为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.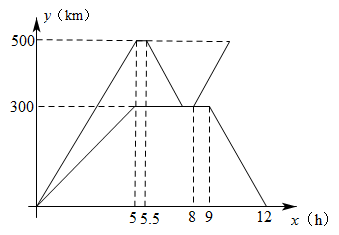 (1)、甲车速度是km/h,乙车出发时速度是km/h;(2)、求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)、乙车出发多少小时,两车之间的距离是120km?请直接写出答案.15. 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )
(1)、甲车速度是km/h,乙车出发时速度是km/h;(2)、求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)、乙车出发多少小时,两车之间的距离是120km?请直接写出答案.15. 已知张强家、体育场、文具店在同一直线上.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列结论不正确的是( )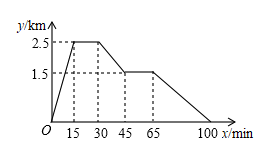 A、张强从家到体育场用了15min B、体育场离文具店1.5km C、张强在文具店停留了20min D、张强从文具店回家用了35min16. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地, 、 分别表示甲、乙两人离开A地的距离 与时间 之间的关系,对于以下说法正确的结论是( )
A、张强从家到体育场用了15min B、体育场离文具店1.5km C、张强在文具店停留了20min D、张强从文具店回家用了35min16. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地, 、 分别表示甲、乙两人离开A地的距离 与时间 之间的关系,对于以下说法正确的结论是( ) A、乙车出发1.5小时后甲才出发 B、两人相遇时,他们离开A地20km C、甲的速度是 ,乙的速度是 D、当乙车出发2小时时,两车相距13km17. 春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是天.
A、乙车出发1.5小时后甲才出发 B、两人相遇时,他们离开A地20km C、甲的速度是 ,乙的速度是 D、当乙车出发2小时时,两车相距13km17. 春耕期间,市农资公司连续8天调进一批化肥,并在开始调进化肥的第七天开始销售.若进货期间每天调进化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个公司的化肥存量s(单位:吨)与时间t(单位:天)之间的函数关系如图所示,则该公司这次化肥销售活动(从开始进货到销售完毕)所用的时间是天.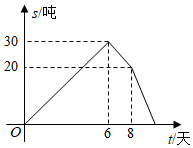 18. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )
18. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系,根据图象提供的信息,以下选项中正确的个数是( )①甲乙两地的距离为450千米;②轿车的速度为70千米/小时;③货车的速度为60千米/小时;④点C的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4四、一次函数与方程(组)
-
19. 直线 ( )过点 , ,则关于 的方程 的解为( )A、 B、 C、 D、20. 如图,已知直线 和直线 交于点 ,则关于x、y的方程组 的解是.
 21. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .
21. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .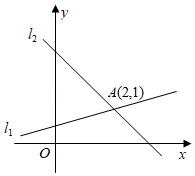 22. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣123. 如图,直线y=x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的点B(0,2)的直线设为y=kx+b.
22. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣123. 如图,直线y=x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的点B(0,2)的直线设为y=kx+b.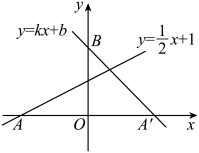 (1)、求点A′的坐标;(2)、确定直线A′B对应的函数表达式.
(1)、求点A′的坐标;(2)、确定直线A′B对应的函数表达式.五、一次函数与一元一次不等式
-
24. 根据图像,可得关于x的不等式的解集是( )
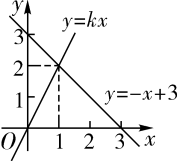 A、 B、 C、 D、25. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 .
A、 B、 C、 D、25. 若一次函数y=kx+b的图象如图所示,则关于kx+b>0的不等式的解集为 . 26. 如图,一次函数 的图象过点 ,则不等式 的解集是( )
26. 如图,一次函数 的图象过点 ,则不等式 的解集是( ) A、 B、 C、 D、27. 如图,直线 和 与x轴分别相交于点 ,点 ,则 解集为( )
A、 B、 C、 D、27. 如图,直线 和 与x轴分别相交于点 ,点 ,则 解集为( )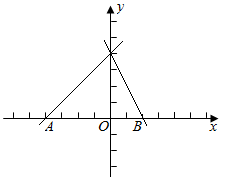 A、 B、 C、 D、 或
A、 B、 C、 D、 或六、一次函数的应用
-
28. 在显示汽车油箱内油量的装置模拟示意图中,电压一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积与电路中总电阻是反比例关系,电流与也是反比例关系,则与的函数关系是( )
 A、反比例函数 B、正比例函数 C、二次函数 D、以上答案都不对29. 如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 .
A、反比例函数 B、正比例函数 C、二次函数 D、以上答案都不对29. 如图,与图中直线y=﹣x+1关于x轴对称的直线的函数表达式是 . 30. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .
30. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .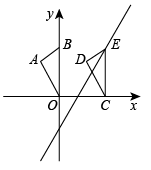 31. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
31. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.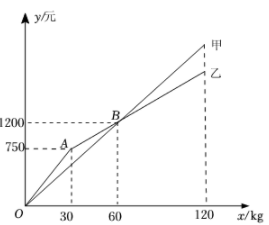 (1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.32. 已知y+3与x-1成正比例,且当x=2时,y=7,求当x=1时,y的值.33. 某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示:
(1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.32. 已知y+3与x-1成正比例,且当x=2时,y=7,求当x=1时,y的值.33. 某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示: (1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?34. 如图,在平面直角坐标系中,直线 交x轴于点 ,交y轴正半轴于点B,且 ,正比例函数 交直线 于点P, 轴于点M, 轴于点 .
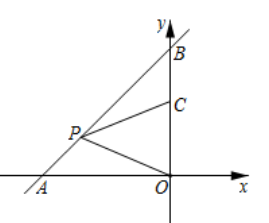
(1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?34. 如图,在平面直角坐标系中,直线 交x轴于点 ,交y轴正半轴于点B,且 ,正比例函数 交直线 于点P, 轴于点M, 轴于点 . (1)、求直线 的函数表达式和点P的坐标;(2)、在y轴负半轴上是否存在点Q,使得 为等腰三角形?若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
(1)、求直线 的函数表达式和点P的坐标;(2)、在y轴负半轴上是否存在点Q,使得 为等腰三角形?若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.