山西省吕梁市孝义市2022-2023学年高二上学期期末数学试题
试卷更新日期:2023-03-02 类型:期末考试
一、单选题
-
1. 是等比数列的前项和, , 则( )A、2 B、4 C、 D、2. 已知函数 , 为的导函数,则的值为( )A、-1 B、0 C、1 D、23. 数列0, , , …的通项公式可以为( )A、 B、 C、 D、4. 已知定义在上的函数的图象如图,则不等式的解集为( )
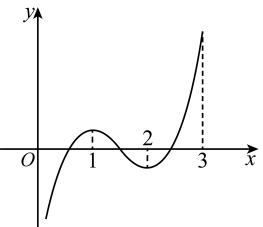 A、 B、 C、 D、5. 已知抛物线 上一点 到其焦点的距离为5,则实数 的值是( )A、-4 B、2 C、4 D、86. 朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升.”其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升.”在该问题中前5天共分发多少升大米?( )A、1170 B、1440 C、1512 D、17727. 是函数的导函数,则( )A、 B、 C、 D、8. 如图,在四棱锥中,平面 , M,N分别为 , 上的点,且 , , 若 , 则的值为( )
A、 B、 C、 D、5. 已知抛物线 上一点 到其焦点的距离为5,则实数 的值是( )A、-4 B、2 C、4 D、86. 朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升.”其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升.”在该问题中前5天共分发多少升大米?( )A、1170 B、1440 C、1512 D、17727. 是函数的导函数,则( )A、 B、 C、 D、8. 如图,在四棱锥中,平面 , M,N分别为 , 上的点,且 , , 若 , 则的值为( )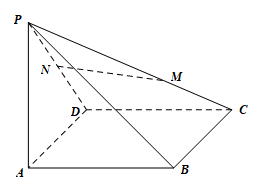 A、 B、 C、1 D、9. 用数学归纳法证明等式 , 从到左端需要增乘的代数式为( )A、 B、 C、 D、10. 已知数列满足 , 且 , , 则( )A、 B、 C、 D、11. 设抛物线 的焦点为F , 过F的直线l与抛物线交于点A,B , 与圆 交于点P,Q , 其中点A,P在第一象限,则 的最小值为( )A、 B、 C、 D、12. 已知函数 , 若关于的不等式恒成立,则实数的取值范围是( )A、 B、 C、 D、
A、 B、 C、1 D、9. 用数学归纳法证明等式 , 从到左端需要增乘的代数式为( )A、 B、 C、 D、10. 已知数列满足 , 且 , , 则( )A、 B、 C、 D、11. 设抛物线 的焦点为F , 过F的直线l与抛物线交于点A,B , 与圆 交于点P,Q , 其中点A,P在第一象限,则 的最小值为( )A、 B、 C、 D、12. 已知函数 , 若关于的不等式恒成立,则实数的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 函数的极值点为 .14. 若函数的导函数为偶函数,则曲线在点处的切线方程为 .15. 已知等差数列满足 , , 记表示数列的前n项和,则当时,n的取值为.16. 对正整数n,函数是小于或等于n的正整数中与n互质的数的数目.此函数以其首名研究者欧拉命名,故被称为欧拉函数.根据欧拉函数的概念,可得 , 数列的前n项和 .
三、解答题
-
17. 已知函数 , 当时,有极小值.(1)、求函数的解析式:(2)、求函数在上的最大值和最小值.18. 已知数列是递增的等比数列,且.(1)、求数列的通项公式;(2)、求数列的前n项和.19. 如图,一海岛O,离岸边最近点B的距离是 ,在岸边距点B 的点A处有一批药品要尽快送达海岛.已知A和B之间有一条快速路,现要用海陆联运的方式运送这批药品,若汽车时速为 ,快艇时速为 .设点C到点B的距离为x.(参考数据: .)
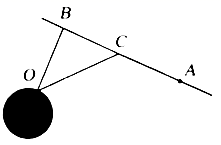 (1)、写出运输时间 关于x的函数;(2)、当点C选在何处时运输时间最短?
(1)、写出运输时间 关于x的函数;(2)、当点C选在何处时运输时间最短?