备战2023年中考数学细点逐一突破真题训练第6章平面直角坐标系及函数、几何相关
试卷更新日期:2023-03-02 类型:二轮复习
一、象限内坐标点特征
-
1. 若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若点 关干x轴的对称点在第四象限,则a的取值范围在数轴上表示为( )A、
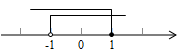 B、
B、 C、
C、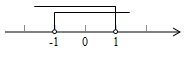 D、
D、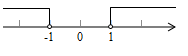 4. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、5. 点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为.6. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
4. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、5. 点A的坐标是(2,﹣3),将点A向上平移4个单位长度得到点A',则点A'的坐标为.6. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )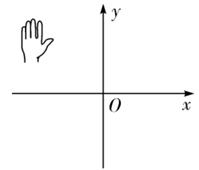 A、 B、 C、 D、7. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.8. 已知点 在第四象限,则m的取值范围是 .
A、 B、 C、 D、7. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.8. 已知点 在第四象限,则m的取值范围是 .二、规律探索类坐标点
-
9. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( )
 A、 B、 C、 D、10. 在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到 ,第二次旋转后得到 ,…,依次类推,则点 的坐标为( )
A、 B、 C、 D、10. 在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到 ,第二次旋转后得到 ,…,依次类推,则点 的坐标为( )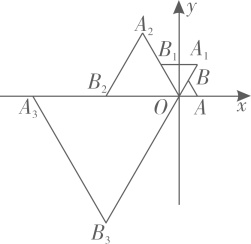 A、 B、 C、 D、11. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .
A、 B、 C、 D、11. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .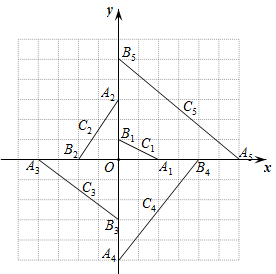 12. 如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4),…,An(n+1,n),构成形如
12. 如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4),…,An(n+1,n),构成形如 ”的图形的阴影部分面积分别表示为S1 , S2 , S3 , …,Sn , 则S2021=.
”的图形的阴影部分面积分别表示为S1 , S2 , S3 , …,Sn , 则S2021=. 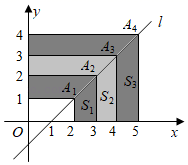 13. 将正整数按如图所示的规律排列下去,用有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示114的有序数对是( )
13. 将正整数按如图所示的规律排列下去,用有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示114的有序数对是( ) A、(15,9) B、(9,15) C、(15,7) D、(7,15)
A、(15,9) B、(9,15) C、(15,7) D、(7,15)三、图形变化相关(相似,圆,解直角三角形等)
-
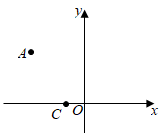
14. 如图,在平面直角坐标系中,点C的坐标为 ,点A的坐标为 ,将点A绕点C顺时针旋转 得到点B,则点B的坐标为.
 15. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
15. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )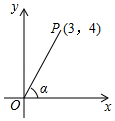 A、 B、 C、 D、16. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
A、 B、 C、 D、16. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )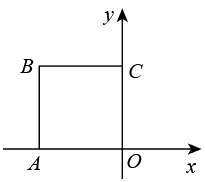 A、 B、 C、 D、17. 如图,在平面直角坐标系中, 的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为( )
A、 B、 C、 D、17. 如图,在平面直角坐标系中, 的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为( )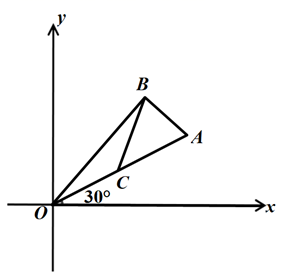 A、 B、 C、 D、18. 如图,在平面直角坐标系中,以 为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则点B的坐标是.
A、 B、 C、 D、18. 如图,在平面直角坐标系中,以 为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则点B的坐标是. 19. 在平面直角坐标系中的位置如图所示,且 ,在 内有一点 ,M , N分别是 边上的动点,连接 ,则 周长的最小值是 .
19. 在平面直角坐标系中的位置如图所示,且 ,在 内有一点 ,M , N分别是 边上的动点,连接 ,则 周长的最小值是 .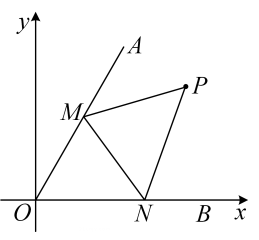
四、函数相关(一次函数,反比例函数)
-
20. 在正比例函数 中,y的值随着x值的增大而增大,则点 在第象限.21. 在平面直角坐标系中,将点向下平移5个单位长度得到点 , 若点恰好在反比例函数的图象上,则的值是.22. 已知直线 与 轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )A、(1,1) B、(1,1)或(1,2) C、(1,1)或(1,2)或(2,1) D、(0,0)或(1,1)或(1,2)或(2,1)23. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图像经过C、D两点.已知平行四边形 的面积是 ,则点B的坐标为( )
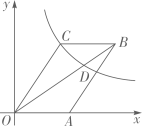 A、 B、 C、 D、
A、 B、 C、 D、五、与概率相关
-
24. 从-3,-2,2这三个数中任取两个不同的数,作为点的坐标,则该点落在第三象限的概率是.25. 从﹣2,4,5这3个数中,任取两个数作为点P的坐标,则点P在第四象限的概率是.
六、网格作图相关(位似,旋转,平移。轴对称等)
-
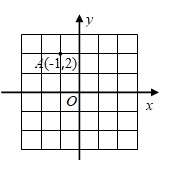
26. 如图,在平面直角坐标系中,将点 向右平移2个单位长度得到点 ,则点 关于 轴的对称点 的坐标是.
 27. 如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是 .
27. 如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是 .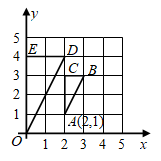 28. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,表示叶片“顶部” , 两点的坐标分别为 , ,则叶杆“底部”点 的坐标为 .
28. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,表示叶片“顶部” , 两点的坐标分别为 , ,则叶杆“底部”点 的坐标为 .


