云南省昭通市昭阳区2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-03-02 类型:期中考试
一、单选题
-
1. 如图是2022年北京冬残奥会吉祥物“雪容融”图案,将图案平移后得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 实数 (相邻两个 之间多一个 ),其中是无理 数的个数是( )个A、 B、 C、 D、3. 下列各式中正确的是( )A、 B、 C、 D、4. 如图,已知直线 , 把含30度的直角三角尺的顶点放在直线b上.若 , 则的度数为( )
2. 实数 (相邻两个 之间多一个 ),其中是无理 数的个数是( )个A、 B、 C、 D、3. 下列各式中正确的是( )A、 B、 C、 D、4. 如图,已知直线 , 把含30度的直角三角尺的顶点放在直线b上.若 , 则的度数为( )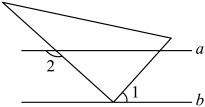 A、138° B、132° C、128° D、122°5. 下列图形中与是对顶角的是( )A、
A、138° B、132° C、128° D、122°5. 下列图形中与是对顶角的是( )A、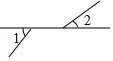 B、
B、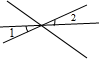 C、
C、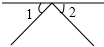 D、
D、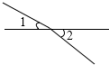 6. 如图所示,不能证明ABCD的是( )
6. 如图所示,不能证明ABCD的是( )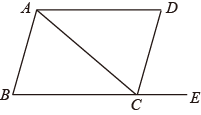 A、∠BAC=∠ACD B、∠ABC=∠DCE C、∠DAC=∠BCA D、∠ABC+∠DCB=180°7. 已知(a﹣2)x|a|﹣1=﹣2是关于x的一元一次方程,则a的值为( )A、﹣2 B、2 C、±2 D、±18. 如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
A、∠BAC=∠ACD B、∠ABC=∠DCE C、∠DAC=∠BCA D、∠ABC+∠DCB=180°7. 已知(a﹣2)x|a|﹣1=﹣2是关于x的一元一次方程,则a的值为( )A、﹣2 B、2 C、±2 D、±18. 如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )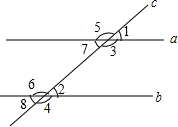 A、①③ B、②④ C、①③④ D、①②③④9. 如图,数轴上与对应的点是( )
A、①③ B、②④ C、①③④ D、①②③④9. 如图,数轴上与对应的点是( )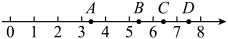 A、点A B、点B C、点C D、点D10. 如图,昭通将向“县县通高铁”的目标进发,着力构建“四横八纵两联多专用”铁路网,在铁路上修建一个站点,设计了A、B、C、D四个,为了县城P到站点的距离近,我们应选择哪个站( )
A、点A B、点B C、点C D、点D10. 如图,昭通将向“县县通高铁”的目标进发,着力构建“四横八纵两联多专用”铁路网,在铁路上修建一个站点,设计了A、B、C、D四个,为了县城P到站点的距离近,我们应选择哪个站( )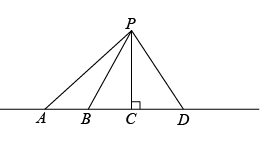 A、站点A B、站点B C、站点C D、站点D11. 下列按一定规律排列的单项式: , , , , , , ..,第个单项式是( )A、 B、 C、 D、12. 已知 , 则 , , , 的大小关系为( )A、 B、 C、 D、
A、站点A B、站点B C、站点C D、站点D11. 下列按一定规律排列的单项式: , , , , , , ..,第个单项式是( )A、 B、 C、 D、12. 已知 , 则 , , , 的大小关系为( )A、 B、 C、 D、二、填空题
-
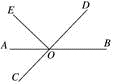
13. “同位角相等”改写成“如果那么”的形式.14. 在平面直角坐标系中,点到y轴的距离是 .15. 如图,直线AB,CD交于点O,OA平分∠EOC,∠EOC∶∠EOD=4∶5,则∠BOD=度.
 16. 3月26日车上挂着“沪昭同心,携手抗疫”的条幅,满载着昭通市上海沪明农特产有限公司、云天宇医疗器械有限公司和云南伯格勒牧业有限公司等多家爱心企业捐赠昭通高原农特产品和时鲜蔬菜等价值434900元的大货车抵达上海.数字434900用科学记数法表示为 .17. 若 , 则的平方根 .18. 按下面的程序计算,若开始输入的值x为正数,最后输出的结果为26,请写出符合条件的所有x的值 .
16. 3月26日车上挂着“沪昭同心,携手抗疫”的条幅,满载着昭通市上海沪明农特产有限公司、云天宇医疗器械有限公司和云南伯格勒牧业有限公司等多家爱心企业捐赠昭通高原农特产品和时鲜蔬菜等价值434900元的大货车抵达上海.数字434900用科学记数法表示为 .17. 若 , 则的平方根 .18. 按下面的程序计算,若开始输入的值x为正数,最后输出的结果为26,请写出符合条件的所有x的值 .
三、解答题
-
19. 计算:(1)、(2)、20. 如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
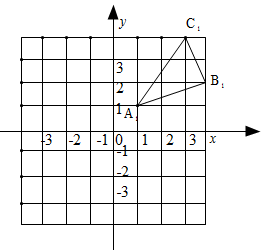 (1)、请画出△ABC,并写出点A、B、C的坐标;(2)、求出△AOA1的面积.21. 如图,已知 , , . 求证: . 请你完成下列填空,把证明过程补充完整
(1)、请画出△ABC,并写出点A、B、C的坐标;(2)、求出△AOA1的面积.21. 如图,已知 , , . 求证: . 请你完成下列填空,把证明过程补充完整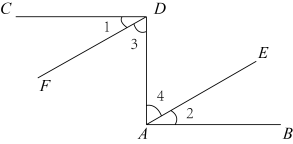
证明:∵ ▲ , ▲
∴ , ( ),
∴ , .
又∵ ,
∴( ),
∴( ).
22. 阅读下面的文字并解答问题:我们知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,但我们知道的整数部分是1,于是用来表示的小数部分.请解答:
(1)、的整数部分是;的小数部分是 .(2)、如果的小数部分是a,的整数部分是b,求的值.23. 为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学 元购进甲、乙两种医用口罩共计 盒,甲,乙两种口罩的售价分别是 元/盒, 元/盒;甲,乙两 种口罩的数量分别是 个/盒, 个/盒.(1)、求新希望中学甲、乙两种口罩各购进了多少盒?(2)、按照教育局要求,学校必须储备两周的用量,新希望中学师生共计 人,每人每天 个口罩,问购买的口罩数量是否能满足教育局的要求?24. 如图,已知直线l1∥l2 , 且l3和l1 , l2分别交于A,B两点,点P在AB上. .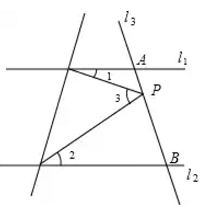 (1)、试找出∠1,∠2,∠3之间的关系并说出理由;(2)、如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化;(3)、如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合) .
(1)、试找出∠1,∠2,∠3之间的关系并说出理由;(2)、如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化;(3)、如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合) .