云南省昭通市永善县2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-02 类型：期中考试

进入出卷网下载

一、单选题

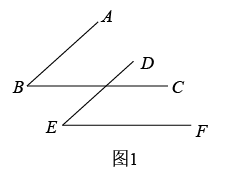
1. 在下列四个图案中，能用平移变换来分析其形成过程的图案是（）

A、 B、 C、 D、

查看试题解析
2. 已知点 $P (- 1 ， a)$ 在第二象限，则 $a$ 的取值范围是（）

A、 $a = 0$ B、 $a > 1$ C、 $a > 0$ D、 $a < 0$

查看试题解析
3. 如果直径为1个单位长度的圆上一点P从数轴上表示3的点A出发，沿数轴向左滚动一周，圆上这一点到达数轴上另一点B，则B点表示的实数为（）．

A、 $π - 3$ B、 $3 - π$ C、 $2 π - 3$ D、 $3 - 2 π$

查看试题解析
4. 估计 $\sqrt{7} + 2$ 的大小应在（）

A、2～3之间 B、4～5之间 C、3～4之间 D、6～7之间

查看试题解析
5. 如图， $A C ⊥ B C$ ， $A C = 6.3$ ，若点P在直线BC上，则AP的长可能是（）

A、4 B、5 C、6 D、7

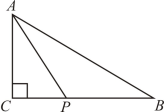查看试题解析
6. 如图，点 $E$ 在 $C D$ 的延长线上，下列条件中不能判定 $A B ∥ C D$ 的是（）

A、 $∠ B + ∠ B D C = 180 °$ B、 $∠ 3 = ∠ 4$ C、 $∠ 5 = ∠ B$ D、 $∠ 1 = ∠ 2$

查看试题解析
7. 下列说法中，错误的有（）
①两点确定一条直线；
②如果两条直线都和第三条直线垂直，那么这两条直线互相平行；
③如果两个角相加等于180°，那么这两个角互余；
④如果两条直线没有公共点，那么这两条直线一定平行．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图：下列四个判断中，正确的个数是（）．
①∠1的内错角只有∠4
②∠1的同位角是∠B
③∠1的同旁内角是∠3、∠E、∠ACD
④图中∠B的同位角共有4个

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 若 $\sqrt{2} = 1.414 ， \sqrt{a} = 14.14$ ，则a的值为（）．

A、20 B、200 C、2000 D、0.02

查看试题解析
10. 若 $0 < x < 1$ ，则 $x^{2}$ 、 $x$ 、 $\sqrt{x}$ 、 $\sqrt[3]{x}$ 这四个数中（）．

A、 $\sqrt[3]{x}$ 最大， $x^{2}$ 最小 B、x最大， $\sqrt[3]{x}$ 最小 C、 $x^{2}$ 最大， $\sqrt[3]{x}$ 最小 D、x最大， $x^{2}$ 最小

查看试题解析
11. 有一个数值转换器原理如下：当输入x=16时，输出的数是（）

A、8 B、2 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
12. 已知三角形的三个顶点坐标分别为(－2，1)，(2，3)，(－3，－1)，把这个三角形运动到一个确定位置，在下列各点的坐标中，是经过平移得到的是（）

A、(0，3)，(0，1)，(－1，－1) B、(－3，2)，(3，2)，(－4，0) C、(1，－2)，(3，2)，(－1，－3) D、(－1，3)，(3，5)，(－2，1)

查看试题解析

二、填空题

13. 在y轴上，若点M与点N（0，3）的距离是6，则点M的坐标是．

查看试题解析
14. $\sqrt[3]{8}$ 的平方根是； $- 1^{2}$ 的立方根是．

查看试题解析
15. 如图，如果AB//CD，那么 $∠ B A E + ∠ A E C + ∠ E C D =$ $°$ .

查看试题解析
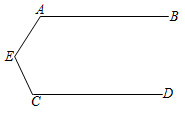16. 如图，把一张长方形纸条ABCD沿EF折叠，若∠1=62°，则∠AEG=°．

查看试题解析
17. 如图，在直角坐标系中，已知点 $A (- 3 ， - 1)$ ，点 $B (- 2 ， 1)$ ，平移线段AB，使点A落在 $A_{1} (0 ， - 1)$ ，点B落在点B₁ ，则点B₁的坐标为．

查看试题解析
18. 如图，在一块长为a米、宽为b米的长方形地上，有一条弯曲的柏油马路，马路的任何地方的水平宽度都是2米，其他部分都是草地，则草地的面积为平方米．

查看试题解析

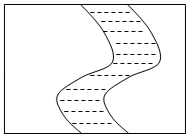
三、解答题

19. 计算：

(1)、 $\sqrt{49} + \sqrt[3]{- 8} + \sqrt{{(- 5)}^{2}}$

(2)、 $- 1^{4} + | \sqrt{3} - 2 | + \sqrt{3}$

查看试题解析
20. 把下列各数填入相应的大括号中：
0.3， $- 1$ ， $\frac{π}{2}$ ， $\sqrt{49}$ ， 0， $\sqrt[3]{- 8}$ ， 3.14， $\frac{22}{7}$ ， $- \sqrt[3]{\frac{8}{27}}$ ， $+ \sqrt{27}$ ， $\frac{\sqrt{64}}{2}$ ， 0.125， $| 1 - \sqrt{3} |$ ， $\sqrt[3]{- 11}$
负数集合{             …}；
整数集合{             …}；
有理数集合{             …}；
无理数集合{             …}．

查看试题解析
21. 如图，在 $8 \times 8$ 的正方形网格中，点 $P$ 是 $∠ A O B$ 的边 $O B$ 上的一点．

(1)、过点 $M$ 画 $O A$ 的平行线 $M N$ ；

(2)、过点 $P$ 画 $O B$ 的垂线，交 $O A$ 于点 $C$ ；

(3)、点 $C$ 到直线 $O B$ 的距离是线段的长度．

(4)、比较线段 $P C$ 与 $O C$ 的大小，并说明理由．

查看试题解析
22. 请将下列题目中横线上的证明过程和依据补充完整：
如图，点 $B$ 在 $A G$ 上，AG $∥$ CD， $C F$ 平分 $∠ B C D$ ， $∠ A B E = ∠ B C F$ ， $B E ⊥ A F$ 于点 $E$ ．求证： $∠ F = 90 °$ ．
证明： $∵$ AG $∥$ CD，
$∴ ∠ A B C = ∠ B C D$ （          ）
$∵ ∠ A B E = ∠ B C F$ ，
$∴ ∠ A B C - ∠ A B E = ∠ B C D - ∠ B C F$ ，
即 $∠ C B E = ∠ D C F$ ，
$∵ C F$ 平分 $∠ B C D$ ，
$∴ ∠ B C F = ∠ D C F$ （          ）
$∴$   ▲   $= ∠ B C F$ ．
∴BC $∥$ CF（          ）
$∴$   ▲   $= ∠ F$ ．
$∵ B E ⊥ A F$ ，
$∴$   ▲   $= 90 °$ （          ）．
$∴ ∠ F = 90 °$ ．

查看试题解析
23. 已知， $∠ A B C$ 和 $∠ D E F$ 中， $A B ∥ D E$ ， $B C ∥ E F$ ．试探究：

(1)、如图1，写出 $∠ B$ 与 $∠ E$ 的关系，并说明理由；

(2)、如图2，写出 $∠ B$ 与 $∠ E$ 的关系，并说明理由；

(3)、根据上述探究，请归纳得到一个真命题．

查看试题解析
24. 如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（6，c）三点，其中a，b，c满足关系式|a-2|+（b-3）²+ $\sqrt{c - 4}$ =0，

(1)、求A．B．C的坐标；

(2)、求三角形ABC的面积；

(3)、在y轴上是否存在点P，使三角形APC的面积与三角形ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析