云南省文山壮族苗族自治州砚山县十校联考2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-02 类型：期中考试

进入出卷网下载

一、填空题

1. 计算： ${(π - 3.14)}^{0} =$ .

查看试题解析
2. 如图是一把剪刀，其中∠1＝40°，则∠2＝，其理由是

查看试题解析
3. 如图，已知直线 $a ∥ b$ ，若 $∠ 1 = 40 °$ ，则 $∠ 2 =$ ．

查看试题解析
4. 一辆汽车以 $60 k m / h$ 的速度匀速行驶，行驶的路程为 $s k m$ ，行驶的时间为 $t h$ ， s与t的关系式为．

查看试题解析
5. 若 $m - n = 2$ ， $m + n = 5$ ，则 $m^{2} - n^{2}$ 的值为．

查看试题解析
6. 如图所示 $， a / / b$ ，一个三角尺的直角顶点放在直线 $b$ 上，量得 $∠ 1 = 6 0^{°}$ ，则 $∠ 2 =$ ．

查看试题解析

二、单选题

7. 计算 $x^{3} \cdot x^{3}$ 的结果是（）

A、 $2 x^{3}$ B、 $2 x^{6}$ C、 $x^{6}$ D、 $x^{9}$

查看试题解析
8. 根据北京小客车指标办的通报，截至2017年6月8日24时，个人普通小客车指标的基准中签几率继续创新低，约为0.00122，相当于817人抢一个指标，小客车指标中签难度继续加大．将0.00122用科学记数法表示应为（）

A、1.22×10^－5 B、122×10^－3 C、1.22×10^－3 D、1.22×10^－2

查看试题解析
9. 若代数式 $x^{2} + k x + 64$ 是完全平方式，则k等于（）

A、 $\pm 8$ B、8 C、16 D、 $\pm 16$

查看试题解析
10. 如图，下列条件中能判定 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ B + ∠ B C D = 180 °$ C、 $∠ 1 = ∠ 3$ D、 $∠ 2 = ∠ 4$

查看试题解析
11. “龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉．当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点，用S₁ ， S₂分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事情节相吻合的是（）

A、 B、 C、 D、

查看试题解析
12. 如图，从边长为a的大正方形纸板中挖去一个边长为b的小正方形后，将其裁成四个相同的等腰梯形，然后拼成一个平行四边形，那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（）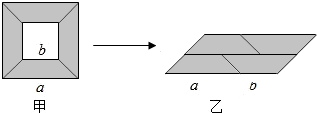

A、 $a^{2} - b^{2} = (a - b)^{2}$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
13. 若 $(m - n)^{2} = 24 ， m n = 2$ ，则 $m^{2} + n^{2}$ 的值为（）

A、26 B、24 C、20 D、28

查看试题解析
14. 现定义运算“△”，对于任意有理数a，b，都有a△b＝a²－ab＋b.例如：3△5＝3²－3×5＋5＝－1，由此可知（x－1）△（2＋x）等于（）

A、2x－5 B、2x－3 C、－2x＋5 D、－2x＋3

查看试题解析

三、解答题

15. 计算：

(1)、 ${(- 3 x y^{2})}^{2} \cdot 4 x y + 6 x^{3} y^{3}$ ；

(2)、 $(- 1)^{2021} + {(\frac{1}{2})}^{- 2} - (3.14 - π)^{0}$ ；

查看试题解析
16. 简便计算：

(1)、 $2021 \times 2019 - 202 0^{2}$ ；

(2)、 ${(\frac{3}{4})}^{2022} \times {(- 1 \frac{1}{3})}^{2022}$

查看试题解析
17. 先化简，再求值： $2 b^{2} + (a + b) (a - b) - (a - b)^{2}$ ，其中 $a = - 5 ， b = \frac{1}{2}$ ．

查看试题解析
18. 如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1＝72°，求∠2的度数．

查看试题解析
19. 已知 $2 a^{2} + 3 a - 3 = 0$ ，求 $3 a (2 a + 1) - (2 a + 1) (2 a - 1)$ 的值．

查看试题解析
20. 填空，完成下列证明过程，并在括号中注明理由．
如图，已知∠CGD=∠CAB，∠1=∠2，求证：∠ADF+∠CFE=180°

证明：∵∠CGD=∠CAB

∴DG∥      ▲ （）

∴∠1=      ▲ （）

∵∠1=∠2

∴∠2=∠3（）

∴EF∥      ▲ （）

∴∠ADF+∠CFE=180°（）

查看试题解析
21. 某路公交车每月有x人次乘坐，每月的收入为y元，每人次乘坐的票价相同，下面的表格是y与x的部分数据．

(1)、下表中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

(2)、请将表格补充完整．
x/人次
500
1000
1500
2000
2500
3000
…
y/元
1000
2000
4000
6000
…

(3)、写出y与x的关系式，若该路公交车每月的收入费用为14000元，则每月乘坐该路公交车要达到多少人次？

查看试题解析
22. 如图，哈市某小区有一块长为（2a+3b）米，宽为（2a-3b）米的长方形地块，角上有四个边长为（a-b）米的小正方形空地，开发商计划将阴影部分进行绿化．

(1)、用含有a、b的式子表示绿化的总面积（结果写成最简形式）．

(2)、若a＝20，b＝10，绿化成本为50元/平方米，则完成绿化共需要多少元钱？

查看试题解析
23. 如图①②， $∠ B$ ， $∠ E$ 的两边分别平行．

(1)、在图①中， $∠ B$ 与 $∠ E$ 的两边相交于点O，G两点， $∠ B$ 与 $∠ E$ 有什么数量关系？为什么？

(2)、在图②中， $∠ B$ 与 $∠ E$ 的一边相交于点O， $∠ B$ 与 $∠ E$ 有什么数量关系？为什么？

(3)、由（1）（2）你能得出什么结论？用一句话概括你得到的结论．

查看试题解析

x/人次	500	1000	1500	2000	2500	3000	…
y/元	1000	2000		4000		6000	…