辽宁省大连市高新园区名校联盟2021-2022学年七年级下学期 期中考试数学试题
试卷更新日期:2023-03-02 类型:期中考试
一、单选题
-
1. 在下面四个数中,是无理数的是( )A、3.1415 B、 C、 D、2. 下列各图中,与是对顶角的是( )A、
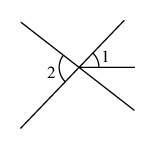 B、
B、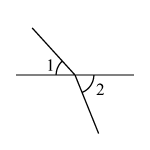 C、
C、 D、
D、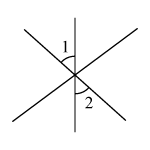 3. 在平面直角坐标中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若是关于x、y的二元一次方程ax-5y=1的解,则a的值为( )A、-5 B、-1 C、9 D、115. 如图,直线 , 直角的直角顶点在直线上,若 , 则的度数为( )
3. 在平面直角坐标中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若是关于x、y的二元一次方程ax-5y=1的解,则a的值为( )A、-5 B、-1 C、9 D、115. 如图,直线 , 直角的直角顶点在直线上,若 , 则的度数为( )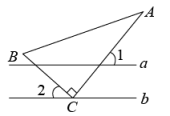 A、 B、 C、 D、6. 已知x,y满足方程组 , 则的值为( )A、-2 B、-3 C、2 D、37. 在平面直角坐标系中,点在第四象限,距离轴个单位长度,距离轴个单位长度.则点的坐标是( )A、 B、 C、 D、8. 如图,数轴上表示实数的点可能是( )
A、 B、 C、 D、6. 已知x,y满足方程组 , 则的值为( )A、-2 B、-3 C、2 D、37. 在平面直角坐标系中,点在第四象限,距离轴个单位长度,距离轴个单位长度.则点的坐标是( )A、 B、 C、 D、8. 如图,数轴上表示实数的点可能是( ) A、点M B、点N C、点P D、点Q9. 八块相同的长方形地砖拼成一个长方形,每块小长方形地砖的面积等于( )
A、点M B、点N C、点P D、点Q9. 八块相同的长方形地砖拼成一个长方形,每块小长方形地砖的面积等于( ) A、625 B、650 C、675 D、70010. 下列命题:①已知直线a、b,若a⊥b, , 则:②在同一平面内,两条直线的位置关系只有相交和平行两种;③过一点有且只有一条直线与已知直线平行;④已知直线a,b,如果 , , 那么 , 其中正确的命题是( )A、②和④ B、①和② C、②和③ D、①和④
A、625 B、650 C、675 D、70010. 下列命题:①已知直线a、b,若a⊥b, , 则:②在同一平面内,两条直线的位置关系只有相交和平行两种;③过一点有且只有一条直线与已知直线平行;④已知直线a,b,如果 , , 那么 , 其中正确的命题是( )A、②和④ B、①和② C、②和③ D、①和④二、填空题
-
11. .12. 在平面直角坐标系中,将点向右平移4个单位长度,再向下平移3个单位长度所得点的坐标为 .13. 如图,直线AB与直线CD相交于点O,MO⊥AB,垂足为O,已知∠AOD=136°,则∠COM的度数为 .
 14. 《九章算术》原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?译文:现有一些人共买一个物品,每人出8钱,还盈余3钱;每人出7钱,则还差4钱,问共多少人,物品价格多少钱?设共有x人,物品的价格是y钱,则可列方程组为·15. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律经过第2022次运动后,动点P的坐标是 .
14. 《九章算术》原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?译文:现有一些人共买一个物品,每人出8钱,还盈余3钱;每人出7钱,则还差4钱,问共多少人,物品价格多少钱?设共有x人,物品的价格是y钱,则可列方程组为·15. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律经过第2022次运动后,动点P的坐标是 . 16. 如图,将一长方形纸条首先沿着EF进行第一次折叠,使得C,D两点落在、的位置,再将纸条沿着GF折叠(GF与BC在同一直线上),使得、分别落在、的位置.若 . 则= .
16. 如图,将一长方形纸条首先沿着EF进行第一次折叠,使得C,D两点落在、的位置,再将纸条沿着GF折叠(GF与BC在同一直线上),使得、分别落在、的位置.若 . 则= .
三、解答题
-
17. 计算: .18.(1)、解方程:;(2)、解方程组: .19. 如图,直线AB、CD相交于点O,OE平分 , , 且 . 求和的度数.
 20. 在平面直角坐标系中,三角形ABC经过平移得到三角形 . 位置如图所示.
20. 在平面直角坐标系中,三角形ABC经过平移得到三角形 . 位置如图所示. (1)、分别写出点A,的坐标:A , ;(2)、三角形的面积为 .(3)、若点M(m,4-n)是三角形ABC内部一点,则平移后对应点的坐标为(2m-8,n-4),求m和n的值.21. 如图,用两个边长为cm的小正方形拼成一个大的正方形.
(1)、分别写出点A,的坐标:A , ;(2)、三角形的面积为 .(3)、若点M(m,4-n)是三角形ABC内部一点,则平移后对应点的坐标为(2m-8,n-4),求m和n的值.21. 如图,用两个边长为cm的小正方形拼成一个大的正方形. (1)、求大正方形的边长:(2)、若沿此大正方形边长的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为48?22. 疫情期间为保护学生和教师的健康,某学校储备“抗疫物资”用29000元购进甲、乙两种医用口罩共计900盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒.(1)、求甲、乙两种口罩各购进了多少盒?(2)、现已知甲,乙两种口罩的数量分别是20个/盒,25个/盒,按照市教育局要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足市教育局的要求?23. 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶派生点”(其中a为常数,且a≠0).例如:点P(1,2)的“2阶派生点”为点Q(2×1+2,1+2×2),即点Q(4,5).(1)、若点P的坐标为(-1,4),则它的“3阶派生点”的坐标为;(2)、若点P的“5阶派生点”的坐标为(-9,3),求点P的坐标;(3)、若点P(m+1,2m-1)先向左平移3个单位长度,再向上平移2个单位长度后得到了点 , 点的“-3阶派生点”位于坐标轴上,求点的坐标.24. 某公司筹集了120吨的救灾物资运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载).
(1)、求大正方形的边长:(2)、若沿此大正方形边长的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为48?22. 疫情期间为保护学生和教师的健康,某学校储备“抗疫物资”用29000元购进甲、乙两种医用口罩共计900盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒.(1)、求甲、乙两种口罩各购进了多少盒?(2)、现已知甲,乙两种口罩的数量分别是20个/盒,25个/盒,按照市教育局要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足市教育局的要求?23. 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶派生点”(其中a为常数,且a≠0).例如:点P(1,2)的“2阶派生点”为点Q(2×1+2,1+2×2),即点Q(4,5).(1)、若点P的坐标为(-1,4),则它的“3阶派生点”的坐标为;(2)、若点P的“5阶派生点”的坐标为(-9,3),求点P的坐标;(3)、若点P(m+1,2m-1)先向左平移3个单位长度,再向上平移2个单位长度后得到了点 , 点的“-3阶派生点”位于坐标轴上,求点的坐标.24. 某公司筹集了120吨的救灾物资运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载).车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
200
250
300
(1)、全部救灾物资可用甲型车8辆,乙型车5辆,丙型车辆来运送;(2)、若全部物资都用甲、乙两种车型来运送,需运费4100元,问分别需甲、乙两种车型各几辆?(3)、为了节省运费,公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,分别求出三种车型的辆数,并求出此时的运费.25. 已知直线ABCD,点E在直线AB、CD之间,点M、N分别在直线AB、CD上.

 (1)、如图1,直线GH过点E,分别与直线AB、CD交于点G、H,∠AME=∠GND,求证:∠NGH+∠MEH=180°;(2)、如图2,点F在直线CD上,ME、NE分别平分∠AMF、∠MNF,若∠FMN=2∠MEN,求∠MEN的度数;(3)、如图3,MQ平分∠AME,MH平分∠BME,GN平分∠ENC.直线GN与MH交于点H,NK平分∠END,NFMQ.求证:∠MHG=∠KNF.
(1)、如图1,直线GH过点E,分别与直线AB、CD交于点G、H,∠AME=∠GND,求证:∠NGH+∠MEH=180°;(2)、如图2,点F在直线CD上,ME、NE分别平分∠AMF、∠MNF,若∠FMN=2∠MEN,求∠MEN的度数;(3)、如图3,MQ平分∠AME,MH平分∠BME,GN平分∠ENC.直线GN与MH交于点H,NK平分∠END,NFMQ.求证:∠MHG=∠KNF.