辽宁省本溪市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算中正确的是（）

A、 ${(- a^{2})}^{3} = - a^{5}$ B、 $a^{3} \cdot a^{4} = a^{12}$ C、 $3 a^{2} - 2 a^{2} = 1$ D、 $a^{6} \div a^{2} = a^{4}$

查看试题解析
2. 下列长度的三根小木棒能构成三角形的是（）

A、2cm，3cm，5cm B、7cm，4cm，2cm C、3cm，4cm，5cm D、3cm，4cm，8cm

查看试题解析
3. $△ A B C$ 的三角之比是 $1 ： 2 ： 3$ ，则 $△ A B C$ 是（）．

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
4. 如图所示，过点P画直线a的平行线b的作法的依据是（）

A、两直线平行，同位角相等 B、同位角相等，两直线平行 C、两直线平行，内错角相等 D、内错角相等，两直线平行

查看试题解析
5. 如图，在△ABC中，BC边上的高为（）

A、AD B、BE C、BF D、CG

查看试题解析
6. 下列算式能用平方差公式计算的是（）

A、 $(2 x - y) (- 2 x + y)$ B、 $(2 x + 1) (- 2 x - 1)$ C、 $(3 a + b) (3 b - a)$ D、 $(- m - n) (- m + n)$

查看试题解析
7. 若长方形的面积是 $2 a^{2} - 2 a b + 6 a$ ，一边长为2a，则这个长方形的周长是（）

A、 $a - b + 3$ B、 $2 a - 2 b + 6$ C、 $6 a - 2 b + 6$ D、 $3 a - b + 3$

查看试题解析
8. 下列说法正确的是（）

A、直线外一点到这条直线的垂线段叫这点到这条直线的距离 B、一对同旁内角的平分线互相垂直 C、对顶角的平分线在一条直线上 D、一个角的补角可能与它的余角相等

查看试题解析
9. 若A、B、C是直线l上的三点，P是直线l外一点，且PA=6cm，PB=5cm，PC=4cm，则点P到直线l的距离（　　）

A、等于4cm B、大于4cm而小于5cm C、不大于4cm D、小于4cm

查看试题解析
10. 如图1，在矩形ABCD中，点P从点C出发，沿C→D→A→B方向运动至点B处停止.设点P运动的路程为x， $△ P B C$ 的面积为y，已知y关于x的函数关系如图2所示，则长方形ABCD的面积为（）

A、15 B、20 C、25 D、30

查看试题解析

二、填空题

11. 2022年，新型冠状病毒奥密克我毒株继续肆虐全球，病毒的平均直径约是0.00000009米．数据0.00000009科学记数法表示为．

查看试题解析
12. 若 ${(x - 1)}^{0} = 1$ ，则x的取值范围是．

查看试题解析
13. 计算： $2^{2021} \times {(- \frac{1}{2})}^{2022} =$ ．

查看试题解析
14. 如图，将一张长方形纸片按如图所示折叠，如果 $∠ 1 = 56 °$ ，那么 $∠ 2 =$ °．

查看试题解析
15. 若 $4 x^{2} + m x y + y^{2}$ 是一个完全平方式，则m= ．

查看试题解析
16. 使 $(x^{2} + p x) (x - 1)$ 计算结果不含 $x^{2}$ 项，则p的值是．

查看试题解析
17. 如图，在△ABC中，AB=8，AC=5，AD为中线，则△ABD与△ACD的周长之差为．

查看试题解析
18. 如图，点C是射线OA上一点，过C作 $C D ⊥ O B$ ，垂足为D，作 $C E ⊥ O A$ ，垂足为C，交OB于点E．给出下列结论：① $∠ 1$ 是 $∠ D C E$ 的余角；② $∠ A O B = ∠ D C E$ ；③图中互余的角共有3对；④ $∠ A C D = ∠ B E C$ ．其中正确结论有．

查看试题解析

三、解答题

19. 计算：

(1)、 $| - 2 | - {(2 - π)}^{0} + {(\frac{1}{3})}^{- 1}$ ；

(2)、 ${(3 x^{2})}^{2} \cdot (- 4 y^{3}) \div {(6 x y)}^{2}$ ；

(3)、 $10 3^{2} - 102 \times 104$ （简便运算）；

(4)、 $[(2 x - y) (2 x + y) + y (y - 6 x)] \div 2 x$ ．

查看试题解析
20. 先化简，再求值： $4 {(x - 1)}^{2} - (2 x + 3) (2 x - 3)$ ，其中x=-1．

查看试题解析
21. 计算

(1)、已知： $4^{m}$ ＝5， $8^{n}$ ＝3，计算 $2^{2 m + 3 n}$ 的值．

(2)、已知：3x+5y＝8，求 $8^{x} \cdot 3 2^{y}$ 的值．

查看试题解析
22. 本溪市实验中学课外活动小组准备进行“创文明校园”的宣传活动，需要制作宣传单，校园附近有一家印刷社，收费y（元）与印刷数x（张）之间的关系如表：
印刷数量x（张）
…
50
100
200
300
…
收费y（元）
…
7.5
15
30
45
…

(1)、上表反映了和之间的关系，自变量是，因变量是；

(2)、从上表可知收费y（元）与印刷数量x（张）之间关系为：；

(3)、若要印刷10000张宣传单，收费元．

查看试题解析
23. 如图，点D、E在AB上，点F、G分别在BC、CA上，且 $D G ∥ B C$ ， $∠ C D G = ∠ E F B$ .

(1)、试判断直线EF与直线CD的位置关系，并说明理由；

(2)、若 $E F ⊥ A B$ ， $∠ C D G = 56 °$ ，求 $∠ A D G$ 的度数.

查看试题解析
24. 小明家距离学校8千米，今天早晨小明骑车上学途中，自行车突然“爆胎”，恰好路边有便民服务点，几分钟后车修好了，他加快速度骑车到校．我们根据小明的这段经历画了一幅图象，该图描绘了小明行驶路程s与所用时间t之间的函数关系，请根据图象回答下列问题：

(1)、小明骑车行驶了千米时，自行车“爆胎”；修车用了分钟．

(2)、修车后小明骑车的速度为每小时千米．

(3)、小明离家分钟距家6千米．

(4)、如果自行车未“爆胎”，小明一直按修车前速度行驶，那么他比实际情况早到或晚到多少分钟．

查看试题解析
25. 完全平方公式： ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多数学问题．
例如：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解：因为 $a + b = 3$ ，
所以 ${(a + b)}^{2} = 9$ ，即： $a^{2} + 2 a b + b^{2} = 9$ ，
又因为 $a b = 1$
所以 $a^{2} + b^{2} = 7$
根据上面的解题思路与方法，解决下列问题：

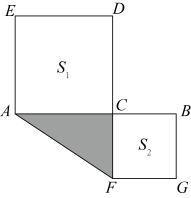
(1)、若 $x + y = 8$ ， $x^{2} + y^{2} = 40$ ，求xy的值；

(2)、填空：若 $(4 - x) x = 3$ ，则 ${(4 - x)}^{2} + x^{2} =$ ．

(3)、如图，点C是线段AB上的一点，以AC、BC为边向两边作正方形，设 $A B = 6$ ，两正方形的面积和 $S_{1} + S_{2} = 18$ ，求图中阴影部分面积.

查看试题解析

印刷数量x（张）	…	50	100	200	300	…
收费y（元）	…	7.5	15	30	45	…