辽宁省阜新市2022年中考数学试卷
试卷更新日期:2023-03-02 类型:中考真卷
一、单选题
-
1. 在实数中,最小的数是( )A、-1 B、2 C、0 D、-22. 在如图所示的几何体中,俯视图和左视图相同的是( )A、
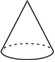 B、
B、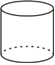 C、
C、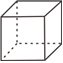 D、
D、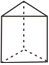 3. 为庆祝神舟十四号发射成功,学校开展航天知识竞赛活动.经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差(单位:分2)如表所示:
3. 为庆祝神舟十四号发射成功,学校开展航天知识竞赛活动.经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差(单位:分2)如表所示:甲
乙
丙
丁
平均数
96
98
95
98
方差
2
0.4
0.4
1.6
如果要选一名成绩好且状态稳定的同学参赛,那么应该选择( )
A、甲 B、乙 C、丙 D、丁4. 已知反比例函数的图像经过点 , 那么该反比例函数图象也一定经过点( )A、 B、 C、 D、5. 不等式组的解集,在数轴上表示正确的是( )A、 B、
B、 C、
C、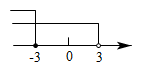 D、
D、 6. 如图, , , 是上的三点,若 , 则的度数是( )
6. 如图, , , 是上的三点,若 , 则的度数是( ) A、 B、 C、 D、7. 如图,是由12个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )
A、 B、 C、 D、7. 如图,是由12个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )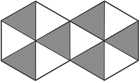 A、 B、 C、 D、8. 我市某区为30万人接种新冠疫苗,由于市民积极配合这项工作,实际每天接种人数是原计划的1.2倍,结果提前20天完成了这项工作.设原计划每天接种万人,根据题意,所列方程正确的是( )A、 B、 C、 D、9. 下列关于二次函数的图像和性质的叙述中,正确的是( )A、点在函数图象上 B、开口方向向上 C、对称轴是直线 D、与直线有两个交点10. 如图,平面直角坐标系中,在直线和轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在轴上,另一条直角边与轴垂直,则第100个等腰直角三角形的面积是( )
A、 B、 C、 D、8. 我市某区为30万人接种新冠疫苗,由于市民积极配合这项工作,实际每天接种人数是原计划的1.2倍,结果提前20天完成了这项工作.设原计划每天接种万人,根据题意,所列方程正确的是( )A、 B、 C、 D、9. 下列关于二次函数的图像和性质的叙述中,正确的是( )A、点在函数图象上 B、开口方向向上 C、对称轴是直线 D、与直线有两个交点10. 如图,平面直角坐标系中,在直线和轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在轴上,另一条直角边与轴垂直,则第100个等腰直角三角形的面积是( )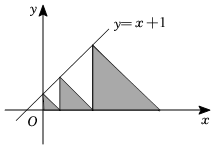 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 一副三角板如图摆放,直线 , 则的度数是 .
 13. 如图,在矩形中,是边上一点,且 , 与相交于点 , 若的面积是 , 则的面积是 .
13. 如图,在矩形中,是边上一点,且 , 与相交于点 , 若的面积是 , 则的面积是 . 14. 在创建“文明校园”的活动中,班级决定从四名同学(两名男生,两名女生)中随机抽取两名同学担任本周的值周长,那么抽取的两名同学恰好是一名男生和一名女生的概率是 .15. 如图,在中, , , 将绕点逆时针旋转 , 得到 , 则点到的距离是 .
14. 在创建“文明校园”的活动中,班级决定从四名同学(两名男生,两名女生)中随机抽取两名同学担任本周的值周长,那么抽取的两名同学恰好是一名男生和一名女生的概率是 .15. 如图,在中, , , 将绕点逆时针旋转 , 得到 , 则点到的距离是 .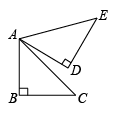 16. 快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离与行驶时间之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 .
16. 快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离与行驶时间之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 .
三、解答题
-
17. 先化简,再求值: , 其中 .18. 当我们将一条倾斜的直线进行上下平移时,直线的左右位置也发生着变化.下面是关于“一次函数图象平移的性质”的探究过程,请补充完整.
 (1)、如图1,将一次函数y=x+2的图像向下平移1个单位长度,相当于将它向右平移了个单位长度;(2)、将一次函数的图像向下平移1个单位长度,相当于将它向(填“左”或“右”)平移了个单位长度;(3)、综上,对于一次函数的图像而言,将它向下平移个单位长度,相当于将它向(填“左”或“右”)(时)或将它向(填“左”或“右”)(时)平移了个单位长度,且 , , 满足等式 .19. 如图,在中, , 是边上一点,以为圆心,为半径的圆与相交于点 , 连接 , 且 .
(1)、如图1,将一次函数y=x+2的图像向下平移1个单位长度,相当于将它向右平移了个单位长度;(2)、将一次函数的图像向下平移1个单位长度,相当于将它向(填“左”或“右”)平移了个单位长度;(3)、综上,对于一次函数的图像而言,将它向下平移个单位长度,相当于将它向(填“左”或“右”)(时)或将它向(填“左”或“右”)(时)平移了个单位长度,且 , , 满足等式 .19. 如图,在中, , 是边上一点,以为圆心,为半径的圆与相交于点 , 连接 , 且 . (1)、求证:是的切线;(2)、若 , , 求的长.20. 某校为提高学生的综合素质,准备开设“泥塑”“绘画”“书法”“街舞”四门校本课程,为了解学生对这四门课程的选择情况(要求每名学生只能选择其中一门课程),学校从七年级学生中随机抽取部分学生进行问卷调查,根据调查结果绘制成如图所示的两幅不完整的统计图.
(1)、求证:是的切线;(2)、若 , , 求的长.20. 某校为提高学生的综合素质,准备开设“泥塑”“绘画”“书法”“街舞”四门校本课程,为了解学生对这四门课程的选择情况(要求每名学生只能选择其中一门课程),学校从七年级学生中随机抽取部分学生进行问卷调查,根据调查结果绘制成如图所示的两幅不完整的统计图.
请你依据图中信息解答下列问题:
(1)、参加此次问卷调查的学生人数是人,在扇形统计图中,选择“泥塑”的学生所对应的扇形圆心角的度数是;(2)、通过计算将条形统计图补充完整;(3)、若该校七年级共有600名学生,请估计七年级学生中选择“书法”课程的约有多少人?21. 如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度 , 在居民楼前方有一斜坡,坡长 , 斜坡的倾斜角为 , . 小文在C点处测得楼顶端A的仰角为 , 在D点处测得楼顶端A的仰角为(点A,B,C,D在同一平面内).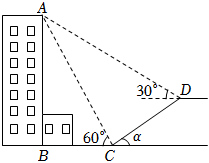 (1)、求C,D两点的高度差;(2)、求居民楼的高度 . (结果精确到 , 参考数据:)22. 某公司引入一条新生产线生产A,B两种产品,其中A产品每件成本为100元,销售价格为120元,B产品每件成本为75元,销售价格为100元,A,B两种产品均能在生产当月全部售出.(1)、第一个月该公司生产的A,B两种产品的总成本为8250元,销售总利润为2350元,求这个月生产A,B两种产品各多少件?(2)、下个月该公司计划生产A,B两种产品共180件,且使总利润不低于4300元,则B产品至少要生产多少件?23. 已知,四边形是正方形,绕点旋转(), , , 连接 , .
(1)、求C,D两点的高度差;(2)、求居民楼的高度 . (结果精确到 , 参考数据:)22. 某公司引入一条新生产线生产A,B两种产品,其中A产品每件成本为100元,销售价格为120元,B产品每件成本为75元,销售价格为100元,A,B两种产品均能在生产当月全部售出.(1)、第一个月该公司生产的A,B两种产品的总成本为8250元,销售总利润为2350元,求这个月生产A,B两种产品各多少件?(2)、下个月该公司计划生产A,B两种产品共180件,且使总利润不低于4300元,则B产品至少要生产多少件?23. 已知,四边形是正方形,绕点旋转(), , , 连接 , . (1)、如图1,求证:≌;(2)、直线与相交于点 .
(1)、如图1,求证:≌;(2)、直线与相交于点 .如图 , 于点 , 于点 , 求证:四边形是正方形;
如图 , 连接 , 若 , , 直接写出在旋转的过程中,线段长度的最小值.
24. 如图,已知二次函数的图像交轴于点 , , 交轴于点 . (1)、求这个二次函数的表达式;(2)、如图 , 点从点出发,以每秒个单位长度的速度沿线段向点运动,点从点出发,以每秒个单位长度的速度沿线段向点运动,点 , 同时出发.设运动时间为秒().当为何值时,的面积最大?最大面积是多少?(3)、已知是抛物线上一点,在直线上是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点坐标;若不存在,请说明理由.
(1)、求这个二次函数的表达式;(2)、如图 , 点从点出发,以每秒个单位长度的速度沿线段向点运动,点从点出发,以每秒个单位长度的速度沿线段向点运动,点 , 同时出发.设运动时间为秒().当为何值时,的面积最大?最大面积是多少?(3)、已知是抛物线上一点,在直线上是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点坐标;若不存在,请说明理由.