陕西省咸阳市礼泉县2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-03-01 类型：期末考试

进入 出卷网 下载

一、选择题(共8小题，每小题3分，计24分.)

  • 1. -12的倒数是（ ）
    A、112 B、−112 C、12 D、1213

    查看试题解析

  • 2. 如图，平面图形绕直线l旋转一周后，可以得到的立体图形是（ ）

    A、 B、 C、 D、

    查看试题解析

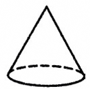  • 3. 从一个多边形的一个顶点出发，可以作2条对角线，则这个多边形是（ ）
    A、三边形 B、四边形 C、五边形 D、六边形

    查看试题解析

  • 4. 若(m−2)x|m|−1=5 是关于x的一元一次方程，则m的值为（ ）
    A、-2 B、-1 C、1 D、2

    查看试题解析

  • 5. 若∠1=50°5′，∠2=50.5°，则∠1与∠2的大小关系是（ ）
    A、∠1=∠2 B、∠2>∠1 C、∠1>∠2 D、无法确定

    查看试题解析

  • 6. 某校开展了“爱阅读”活动，七(1)班统计了1月~6月七(1)班1月~6月课外阅读数量统计图，绘制了折线统计图(如图所示)，则下列说法正确的是（ ）
    全班同学的课外阅读数量(单位：本)

    A、6月份阅读数量最大 B、阅读数量超过40本的月份共有5个月 C、相邻的两个月中，1月到2月的月阅读数量增长最快 D、4月份阅读数量为38本

    查看试题解析

  • 7. 将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成(第6题图)体，则下列序号中不应剪去的是（ ）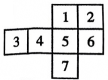

    A、6 B、3 C、2 D、1

    查看试题解析

  • 8. 2022年卡塔尔世界杯于北京时间11月21日0时正式开幕.某足球比赛的记分办法为：胜一场得3分，平一场得1分，负一场得0分.一个队打了14场比赛，负5场，共得19分，那么这个队胜了 （ ）
    A、  3场 B、4场 C、5场 D、6场

    查看试题解析

二、填空题(共5小题，每小题3分，计15分)

  • 9. 泾河是流经礼泉县最大的河流.发源于宁夏泾源县，流经礼泉县的北部和东北部边界，全长25000米.将数据25000用科学记数法表示为.

    查看试题解析

  • 10. 调查礼泉县居民的垃圾分类情况应采用.(填“普查”或“抽样调查”)

    查看试题解析

  • 11. 用一个平面分别去截长方体，圆锥，三棱柱，圆柱，能得到截面是三角形的几何体有个.

    查看试题解析

  • 12. 若关于x、y的多项式x5-m+5y2-2x2+3的次数是3，则式子m2-3m的值为.

    查看试题解析

  • 13. 我国古代《孙子算经》记载了这样一个数学问题：“今有三人共车，二车空；二人共车，九人步.问车有几何?意思是”每3人共乘一辆车，最终剩余2辆车；每2人共乘一辆车，最终有9人无车可乘，则车有辆.

    查看试题解析

三、解答题(共13小题，计81分.)

  • 14. 计算：

    -12+2×( -3)2÷( -6).

    查看试题解析

  • 15. 解方程 2x−13=2x+16−1

    查看试题解析

  • 16. 如图，点A、B、C在同一平面内，利用尺规，按下列要求作图.(不写作法，保留作图痕迹)

    ⑴画射线AB和线段AC；

    ⑵在射线AB上求作一点P，使AP=2AC.

    查看试题解析

  • 17. 已知关于x的一元一次方程ax-2=7与方程2x-1=5的解互为相反数，求a的值.

    查看试题解析

  • 18. 已知A=2x2-2xy-y2 ， B=x2-3xy.
    (1)、化简A-2B的值；
    (2)、当x=-2，y=1时，求A-2B的值.

    查看试题解析

  • 19. 如图，点C是线段AB上的一点，点M是线段AC的中点，点N是线段BC的中点.已知AM=54BC=5cm ， 求MN的长.

    查看试题解析

  • 20. 如图，在一条不完整的数轴上从左到右有点A，B，C，D，其中AD=6，且AB=BC=CD.

    (1)、则BC的长为；
    (2)、若以B为原点，写出点A，C，D所对应的数，并求出它们所对应数的和.

    查看试题解析

  • 21. 用若干个相同的小正方体搭成一个几何体，使它从正面和上面看到的形状如图所示.画出搭成几何体所用正方体最多时从左面看到的形状图.

    查看试题解析

  • 22. 某县质量技术监督局对本县某企业出售的葡萄进行了抽检，从库中任意抽出20箱样品进行检测，每箱的质量超过标准质量(标准质量为10千克)的部分记为正，不足的部分记为负，记录如下表：

    与标准质量的差（千克）

    -0.1

    0

    -0.2

    +0.3

    +0.1

    +0.4

    箱数

    2

    5

    1

    4

    6

    2
    (1)、若每箱与标准质量的差的绝对值小于或等于0.2千克的记为合格产品，则这20箱样品的合格率是多少?
    (2)、这批样品平均每箱质量比标准质量多或少几千克?

    查看试题解析

  • 23. 用火柴棒按图中的方式搭图形.如下图所示：

    图形标号

    ①

    ②

    ③

    ④

    ⑤

    …

    火柴棒根数

    5

    9

    13

    17

    a

    …
    (1)、根据规律填空：a=；
    (2)、按照这种方式搭下去，搭第n个图形需要火柴棒的根数为；(用含n的式子表示)
    (3)、按这种方式搭下去，用(2)中的式子求第多少个图形需要4045根火柴棒?

    查看试题解析

  • 24. 甲、乙两个文具店销售同一种作业本，甲文具店的售价为2.3元/本，乙文具店在购买不超过100本时，售价为2.5元/本，超过100本的部分售价为2.1元/本，只选择其中一家购买，设购买x本(x>100).
    (1)、在乙文具店购买x本需要元；
    (2)、当购买多少本作业本时，在甲、乙两个文具店所需的钱数一样?

    查看试题解析

  • 25. 2022年3月23日，“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣，某校举行了太空科普知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分为如下5组(满分100分)，其中A组：75≤x<80，B组：80≤x<85，C组：85≤x<90，D组：90≤x<95，E组：95≤x<100，并绘制了如下不完整的统计图.

    (1)、本次调查一共随机抽取了名学生的成绩，频数分布直方图中m= ， 扇形统计图中A组占%；
    (2)、补全学生成绩频数分布直方图；
    (3)、若将竞赛成绩在90分及以上的记为优秀，求优秀学生所在扇形对应圆心角的度数.

    查看试题解析

  • 26. 如图，∠AOB=90°，OM平分∠AOC，ON平分∠BOC.

    (1)、若∠BOC=30°，求∠MON的度数；
    (2)、设∠BOC=(2x)°，能否求出∠MON的度数?若能，请求出其值；若不能，请说明理由；
    (3)、若将题干中“∠AOB=90°”改为“∠AOB=α(0°<α<90°)”，其他条件不变，设∠BOC=β，请用含α的式子表示∠MON的度数.

    查看试题解析