陕西省咸阳市礼泉县2022-2023学年九年级上学期期末数学试题
试卷更新日期：2023-03-01 类型：期末考试
一、选择题(共8小题，每小题3分，计24分.)
-
1. 下列给出长度的四条线段中，是成比例线段的是（ ）A、1 ，2，3，4 B、2，3，4，5 C、1 ，2，3，6 D、1 ，3，4，72. 如图所示的物体是一个几何体，其主视图是（ ）
A、
B、
C、
D、
3. 如图，以点O为位似中心，将△ABC放大得到△DEF.若AD=OA，则△ABC与△DEF的周长之比为（ ）
A、1：6 B、1：5 C、1：4 D、1：24. 如图，在矩形ABCD中，对角线AC，BD交于点O，若AC=14，则OB的长为（ ）
A、7 B、6 C、5 D、25. 若关于x的一元二次方程 ( k-2)x2-2x+1=0有两个不相等的实数根，且k为非负整数，则符合条件的k的个数为（ ）A、0个 B、1个 C、2个 D、3个6. 已知反比例函数的图象位于第一、三象限，则m的取值范围是（ ）A、m＞3 B、m＞-3 C、m＜3 D、m＜-37. 如图，是一个可以自由转动的转盘，它被分成三个面积相等的扇形，任意转动转盘两次，当转盘停止后，指针(如果落在分隔线上，则重新转动，直至转到其中一区域)所指颜色相同的概率为（ ）
A、 B、 C、 D、8. 已知点A(x1 ， y1)，B(x2 ， y2)，C(x3 ， y3)都在反比例函数的图象上，若x1＜x2＜0＜x3则y1 ， y2 ， y3的大小关系是（ ）A、y1＜y2＜y3 B、y2＜y1＜y3 C、y3＜y2＜y1 D、y3＜y1＜y2二、填空题(共5小题，每小题3分，计15分)
-
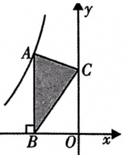
9. 已知关于x的方程x2+3x-m=0的一个根为-2，则m的值是.10. 台灯照射文具盒所形成的影子属于投影.(填“平行”或“中心”)11. 在一个不透明的口袋中装有红、黄两种颜色的球，它们形状大小完全相同，其中5个红球，若干个黄球，从中随机摸出一个球，记下颜色后放回，重复以上过程，经过多次试验发现摸到红球的频率稳定在0.2，据此估计袋中黄球的个数约为个.12. 如图，点A是反比例函数 的图象上的一点，过点A作AB⊥x轴，垂足为B，点C 为y轴上的一点，连接AC、BC，若△ABC的面积为3，则k的值是.
13. 如图，菱形ABCD的边长为4，∠BAD=60°，点E是边AB上一动点(不与点A、B重合)，过点E作EF∥BC交AC于点F，连接DF，当△ADF是等腰三角形时，AE的长为.
三、解答题(共13小题，计81分.)
-
14. 解方程：5x2+2x-1 =0.15. 已知x1 ， x2是关于x的方程x2-2x+m-2=0的两个实数根，若3x1+3x2-x1x2=5，求m 的值.
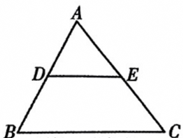16. 如图所示，点D、E分别在AB、AC上，连接DE，△ADE∽△ABC，已知△ADE和△ABC的相似比是1：2，且△ADE的面积是1，求四边形DBCE的面积.
17. 在工程实施过程中，某工程队接受一项开挖水渠的工程，所需天数y(天)与每天完成工程量x(米)是反比例函数关系，图象如图所示：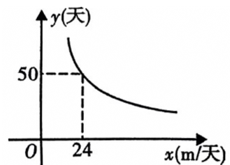
(1)、求y与x之间的函数关系式(2)、若该工程队有4台挖掘机，每台挖掘机每天能够开挖水渠30米，问该工程队需要用多少天才能完成此项任务?18. 按如图所示的方法分别以AB和AC为边作正方形ABDE和正方形AGFC，连接CE、BG，求证：△ACE≌△AGB.
19. 如图，在直角坐标系中，△ABC各顶点的坐标分别为A(-1，1)，B(2，3)，C(0，3).
(1)、以原点O为位似中心，在x轴上方作△ABC的位似图形，与△ABC的相似比为2：1，点A、B、C的对应点分别为(2)、在(1)的条件下，写出点的坐标.20. 为弘扬科学精神，传播航天知识、感悟榜样精神与力量.学校教务处决定开展“飞天梦永不失重，科学梦张力无限”的主题活动，包含了以下四个内容：A.书写观后感；B.演示科学实验；C.绘制手抄报；D.开展主题班会.王老师在四张完全相同的卡片上分别写了A，B，C，D，然后背面朝上放置，搅匀后要求先由八年级派一名代表从中随机抽取一张，记下标号后放回搅匀，再由九年级派一名代表从中随机抽取一张.(1)、八年级代表抽到的主题卡片是绘制手抄报(C)的概率是；(2)、请用列表或画树状图的方法，求两个年级代表抽到的主题卡片中有演示科学实验(B)的概率.21. 如图，P为AB上一点，∠A=∠CPD=∠B，连接CD.
(1)、求证：△ACP∽△BPD(2)、若AP=3，AB=9，AC=8，求BD的长.22. 随着国内新能源汽车的普及，为了适应社会的需求，全国各地都在加快公共充电桩的建设，某省2020年公共充电桩的数量为2万个，2022年公共充电桩的数量为2.88万个.求2020年至2022年该省公共充电桩数量的年平均增长率.23. 小丽想利用所学知识测量旗杆AB的高度，如图，小丽在自家窗边看见旗杆和住宅楼之间有一棵大树DE，小丽通过调整自己的位置，发现半蹲于窗边，眼睛位于C处时，恰好看到旗杆顶端A、大树顶端D在一条直线上，测得EF=4米，BE=12米，眼睛到地面的距离CF为3.5米，已知大树DE的高度为7米，CG⊥AB于点G，AB⊥BF于点B，DE⊥BF于点E，交CG于点H，CF⊥BF于点F.请你根据以上信息帮小丽求出旗杆AB的高度.
24. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且连接CE
(1)、求证：四边形OCED为矩形；(2)、连接AE，若DB=6，AC=8，求AE的长.25. 如图，一次函数y=kx+b与反比例函数y=m/x的图象相交于A、B两点，过点B作BC⊥x轴，垂足为C，连接AC，已知A点的坐标是(2，3)，BC=2.
(1)、求反比例函数与一次函数的关系式；(2)、点P为反比例函数y=m/x图象上的任意一点，若S_POC=3S_ABC，求点P的坐标.26. 如图
(1)、模型建立：如图1，在△ABC中，D是AB上一点，∠ACD=∠B，求证：AC²=AD·AB；(2)、类比探究：如图2，在菱形ABCD中，E、F分别为边BC、DC上的点，且 射线AE交DC的延长线于点M，射线AF交BC的延长线于点N.①求证：. FA2=FC · FM
②若AF=4，CF=2，AM=10，求FN的长.