江苏省徐州市邳州市2022-2023学年九年级上学期期末数学试题
试卷更新日期:2023-03-01 类型:期末考试
一、单选题
-
1. 下列中国传统吉祥图案中,不是中心对称图形的是( )A、
 B、
B、 C、
C、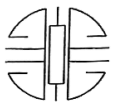 D、
D、 2. 我市某校开展共创文明班,一起向未来的古诗文朗诵比赛活动,有10位同学参加了初赛,按初赛成绩由高到低取前5位进入决赛.如果小王同学知道了自己的成绩后,要判断能否进入决赛,他需要知道这10位同学成绩的( )A、平均数 B、众数 C、中位数 D、方差3. 已知关于x的方程的一个根为 , 则实数b的值为( )A、2 B、 C、3 D、4. 《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:3,5,4,6,3,3,4,则这组数据的众数和中位数分别是( )A、3,4 B、4,3 C、3,3 D、4,45. 如图,在中,D、E分别是和上的点, , 若 , 那么( )
2. 我市某校开展共创文明班,一起向未来的古诗文朗诵比赛活动,有10位同学参加了初赛,按初赛成绩由高到低取前5位进入决赛.如果小王同学知道了自己的成绩后,要判断能否进入决赛,他需要知道这10位同学成绩的( )A、平均数 B、众数 C、中位数 D、方差3. 已知关于x的方程的一个根为 , 则实数b的值为( )A、2 B、 C、3 D、4. 《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:3,5,4,6,3,3,4,则这组数据的众数和中位数分别是( )A、3,4 B、4,3 C、3,3 D、4,45. 如图,在中,D、E分别是和上的点, , 若 , 那么( ) A、 B、 C、 D、6. 如图,在中, , , .以点A为圆心,r为半径作圆,当点C在内且点B在外时,r的值可能是( )
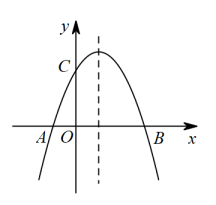
A、 B、 C、 D、6. 如图,在中, , , .以点A为圆心,r为半径作圆,当点C在内且点B在外时,r的值可能是( )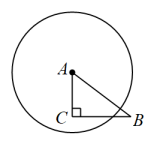 A、3 B、4 C、5 D、67. 二次函数的部分图像如图所示,其对称轴为直线 , 与x轴交于点A,点A的坐标为 , 则的值为( )
A、3 B、4 C、5 D、67. 二次函数的部分图像如图所示,其对称轴为直线 , 与x轴交于点A,点A的坐标为 , 则的值为( )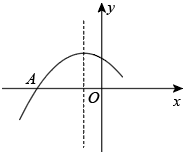 A、 B、0 C、1 D、28. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )
A、 B、0 C、1 D、28. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )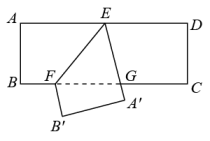 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 方程的根是.10. 二次函数的顶点坐标是.11. 已知圆锥的母线长为5,底面圆的半径为3,则这个圆锥的侧面积是.12. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .13. 如图,点A、B、C在上,且 , 若 , 则的度数为.
 14. 如图,已知大正方形的面积是25,小正方形的面积是1,那么.
14. 如图,已知大正方形的面积是25,小正方形的面积是1,那么. 15. 如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是.
15. 如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是. 16. 如图,正方形的面积为8,以它的对角线的交点为位似中心,作它的位似图形 , 若 , 则四边形的外接圆的周长为.
16. 如图,正方形的面积为8,以它的对角线的交点为位似中心,作它的位似图形 , 若 , 则四边形的外接圆的周长为.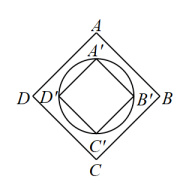 17. 如图,树在路灯O的照射下形成投影 , 已知路灯高 , 树影 , 树与路灯O的水平距离 , 则树的高度长是.
17. 如图,树在路灯O的照射下形成投影 , 已知路灯高 , 树影 , 树与路灯O的水平距离 , 则树的高度长是.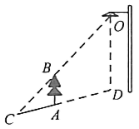 18. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
18. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
三、解答题
-
19.(1)、计算:;(2)、解方程:.20. 某校为丰富课后活动,实现“多彩校园,出彩少年”的教育目标,创建了“诗词雅颂”、“民乐风韵”、“武术雄姿”、“围旗圣手”四个社团(依次记为A、B、C、D).小华和小莉两名同学报名参加社团,一人只能参加一个社团.(1)、小华参加“诗词雅颂”社团的概率是;(2)、请用列表法或画树状图的方法,求小华和小莉两名同学参加同一社团的概率.21. 按照国家视力健康标准,学生视力状况分为:视力正常、轻度视力不良、中度视力不良、重度视力不良四个类别,分别用A、B、C、D表示.某数学兴趣小组为了解本校学生的视力健康状况,从全校1200名学生中随机抽取部分学生,进行视力状况调查,根据调查结果,绘制如下统计图.
抽取的学生视力状况统计图
类别
A
B
C
D
人数
140
m
n
50
 (1)、n=;(2)、调查视力数据的中位数所在类别为类;(3)、该校共有学生1200人,请估算该校学生中,中度视力不良和重度视力不良的总人数.22. 如图、在平面直角坐标系中,的顶点坐标分别为 , , .
(1)、n=;(2)、调查视力数据的中位数所在类别为类;(3)、该校共有学生1200人,请估算该校学生中,中度视力不良和重度视力不良的总人数.22. 如图、在平面直角坐标系中,的顶点坐标分别为 , , . (1)、以原点O为位似中心,在第三象限内画 , 使它与的相似比为2:1;(2)、点的坐标是 , 的面积是.23. “杂交水稻之父”—袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量 公斤的目标,第三阶段实现水稻亩产量 公斤的目标.如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率.24. 如图,点A、B、C在上, , 直线 , , 点O在上.
(1)、以原点O为位似中心,在第三象限内画 , 使它与的相似比为2:1;(2)、点的坐标是 , 的面积是.23. “杂交水稻之父”—袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量 公斤的目标,第三阶段实现水稻亩产量 公斤的目标.如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率.24. 如图,点A、B、C在上, , 直线 , , 点O在上.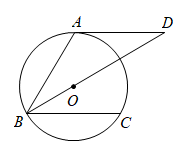 (1)、判断直线与的位置关系,并说明理由;(2)、若的半径为4,求弦的长.25. 2022年中国成功举办了冬奥会和残奥会,吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套30元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是40元时,每天可售出120套;若每套售价提高1元,则每天少卖2套.(1)、设每套售价定为x元,则该商品当天的销售量为件;(2)、设每天销售该套件所获利润为W元,求每套售价定为多少元时,利润最大,最大利润是多少元?
(1)、判断直线与的位置关系,并说明理由;(2)、若的半径为4,求弦的长.25. 2022年中国成功举办了冬奥会和残奥会,吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套30元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是40元时,每天可售出120套;若每套售价提高1元,则每天少卖2套.(1)、设每套售价定为x元,则该商品当天的销售量为件;(2)、设每天销售该套件所获利润为W元,求每套售价定为多少元时,利润最大,最大利润是多少元?